

Up: Rovibrational excitation of HD
The computer code MOLSCAT developed by Hutson & Green
([1995]) has been used in this work. Close-coupling quantal
collision equations are solved for a rotating harmonic oscillator perturbed by
a structureless atom, in this case helium. Different numerical methods are
implemented in the code to solve the coupled, second-order differential
equations. Among the various possibilities, the hybrid modified
LOG-DERIVATIVE/AIRY propagator (Alexander & Manolopoulos
[1987]) and the R-MATRIX propagator
(Stechel et al. [1978]) have been tried, with mutually consistent
results. The potential surface of Muchnik & Russek ([1994]),
relative to the H2-He system, is expressed as a function of the distances
between the three atoms in the system including a range of H2 internuclear
distances adequate to probe the vibrationally excited wave functions, as shown
in Flower et al. ([1998]). The potential surfaces of the
H2-He and HD-He systems are identical from the adiabatic point of view where
nuclei are fixed.
As in the previous related studies (Flower et al. [1998]; Flower &
Roueff [1999]; Roueff & Zeippen [1999]), the facility
provided by the MOLSCAT program to expand the potential in terms of
Legendre polynomials was used. Now, contrary to the H2-He case, the Legendre
expansion for the HD-He interaction contains odd as well as even contributions
of 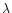 since the system is not symmetric anymore with respect to the
exchange of nuclei within the molecule. In the present collision calculations,
terms up to
since the system is not symmetric anymore with respect to the
exchange of nuclei within the molecule. In the present collision calculations,
terms up to 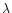 = 15 have been retained in the potential expansion and
vibrational levels up to v = 3 have been included.
= 15 have been retained in the potential expansion and
vibrational levels up to v = 3 have been included.
![\begin{figure}\par\includegraphics[width=8.8cm,clip]{fig1.eps}\end{figure}](/articles/aas/full/2000/06/ds9512/Timg4.gif) |
Figure 1:
Comparison between present (filled points) and rigid rotor
results (Roueff & Zeippen [1999]) (open points) for the de-excitation
collisional cross-sections as a function of the relative center-of-mass
velocity:
a) de-excitation from the J=1 level,
b) de-excitation from the J = 2 level,
c) de-excitation from the J = 3 level |
Table 1:
Labels and energies of HD rovibrational levels used in
the present expansion basis
| J |
v |
E(1) |
E(K) |
|
| 0 |
0 |
0.00 |
0.00 |
|
| 1 |
0 |
89.23 |
128.4 |
|
| 2 |
0 |
267.12 |
384.3 |
|
| 3 |
0 |
532.32 |
765.9 |
|
| 4 |
0 |
883.30 |
1270.7 |
|
| 5 |
0 |
1317.45 |
1895.4 |
|
| 6 |
0 |
1832.55 |
2635.8 |
|
| 7 |
0 |
2424.14 |
3487.5 |
|
| 8 |
0 |
3089.46 |
4445.3 |
|
| 0 |
1 |
3632.568 |
5226.7 |
|
| 1 |
1 |
3717.938 |
5349.6 |
|
| 9 |
0 |
3824.924 |
5503.5 |
|
| 2 |
1 |
3888.082 |
5594.4 |
|
| 3 |
1 |
4141.820 |
5959.5 |
|
| 4 |
1 |
4477.420 |
6442.3 |
|
| 10 |
0 |
4626.133 |
6656.3 |
|
| 5 |
1 |
4892.634 |
7039.8 |
|
| 6 |
1 |
5384.750 |
7747.8 |
|
| 11 |
0 |
5488.828 |
7897.6 |
|
| 7 |
1 |
5950.651 |
8562.1 |
|
| 12 |
0 |
6408.644 |
9221.1 |
|
| 8 |
1 |
6586.873 |
9477.5 |
|
| 0 |
2 |
7087.660 |
10198.1 |
|
| 1 |
2 |
7169.249 |
10315.5 |
|
| 9 |
1 |
7289.669 |
10488.7 |
|
| 2 |
2 |
7331.849 |
10549.4 |
|
| 13 |
0 |
7381.163 |
10620.4 |
|
| 3 |
2 |
7574.313 |
10898.3 |
|
| 4 |
2 |
7894.961 |
11359.7 |
|
| 10 |
1 |
8055.076 |
11590.0 |
|
| 5 |
2 |
8291.609 |
11930.4 |
|
| 14 |
0 |
8401.964 |
12089.2 |
|
| 6 |
2 |
8761.628 |
12606.7 |
|
| 11 |
1 |
8878.973 |
12775.5 |
|
| 7 |
2 |
9301.995 |
13384.2 |
|
| 15 |
0 |
9466.661 |
13621.1 |
|
| 12 |
1 |
9757.136 |
14039.0 |
|
| 8 |
2 |
9909.350 |
14258.1 |
|
| 0 |
3 |
10368.877 |
14919.3 |
|
| 1 |
3 |
10446.746 |
15031.3 |
|
| 16 |
0 |
10570.939 |
15210.0 |
|
| 9 |
2 |
10580.064 |
15223.1 |
|
| 2 |
3 |
10601.922 |
15254.6 |
|
| 13 |
1 |
10685.293 |
15374.5 |
|
| 3 |
3 |
10833.290 |
15587.5 |
|
The integral cross-sections are obtained by summing the partial cross-sections
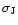 until convergence is reached. A step of 1 is taken for collision
energies smaller than 5000 1. Larger step values may be used for higher
energies since the partial cross-sections vary smoothly with J. This is
fortunate because, as expected, the number of partial cross-sections becomes
very large as collision energy increases. The expansion basis is made of the
first 45 rovibrational levels in HD whose energies, displayed in Table 1, are
taken from Dabrowski & Herzberg ([1976]) and Abgrall et al.
([1982]).
Cross-sections for rovibrational transitions were calculated on a grid of
barycentric collision energies extending from the threshold of the first
rotational level at 89.23 cm-1 up to 100 000 cm-1.
until convergence is reached. A step of 1 is taken for collision
energies smaller than 5000 1. Larger step values may be used for higher
energies since the partial cross-sections vary smoothly with J. This is
fortunate because, as expected, the number of partial cross-sections becomes
very large as collision energy increases. The expansion basis is made of the
first 45 rovibrational levels in HD whose energies, displayed in Table 1, are
taken from Dabrowski & Herzberg ([1976]) and Abgrall et al.
([1982]).
Cross-sections for rovibrational transitions were calculated on a grid of
barycentric collision energies extending from the threshold of the first
rotational level at 89.23 cm-1 up to 100 000 cm-1.


Up: Rovibrational excitation of HD
Copyright The European Southern Observatory (ESO)
![\begin{figure}\par\includegraphics[width=8.8cm,clip]{fig1.eps}\end{figure}](/articles/aas/full/2000/06/ds9512/Timg4.gif)