 |
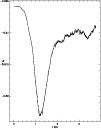
Figure C2: A zoom in the total energy displayed in Fig. C1 revealing the conservation error in the critical phase of the adiabatic shock |
One possible three-dimensional SPH energy-conservation
test is the spherical collapse of an
initially-cold adiabatic-gas, with a radial profile
![]() ([Evrard 1988]; HK89; [Nelson & Papaloizou 1994];
[Steinmetz M. & Müller 1993]), called Evrard's test.
([Evrard 1988]; HK89; [Nelson & Papaloizou 1994];
[Steinmetz M. & Müller 1993]), called Evrard's test.
The initial configuration was obtained by Monte Carlo by
distributing 4096 particles spherically, according to a
1/r radial-profile.
As in HK89, the total mass, M, the cutoff-radius,
R,
and the gravitational constant G are equal to unity,
and the initial specific thermal-energy, u=0.05,
was
homogeneously distributed in the system.
The adopted number of time-bins was 4, starting from a
root time-step,
![]() .
The softening length,
.
The softening length,
![]() ,
was estimated
from Eq. (26), where
both
,
was estimated
from Eq. (26), where
both ![]() and
and
![]() are iteratively calculated during
the initializations.
The aperture parameter
are iteratively calculated during
the initializations.
The aperture parameter ![]() was set as the two-bit floating
was set as the two-bit floating
![]() .
.
Thermal energy was explicitly integrated keeping fixed the entropy:
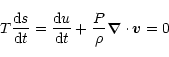 |
(C1) |
Some of the results are shown in Fig. C1 in terms of the evolution
of the
integral energies: total, E, thermal, U, kinetic, K, and potential, ![]() .
The graph in Fig. C1 does agree to other works in literature
(e.g., HK89;
SM93).
The total energy was conserved within
.
The graph in Fig. C1 does agree to other works in literature
(e.g., HK89;
SM93).
The total energy was conserved within ![]() .
The behavior of the total-energy error is illustrated
in Fig. C2, showing that a numerical cooling roughly mimics the
potential
energy rate.
Both total linear and angular momenta were better conserved than one part
in 105.
.
The behavior of the total-energy error is illustrated
in Fig. C2, showing that a numerical cooling roughly mimics the
potential
energy rate.
Both total linear and angular momenta were better conserved than one part
in 105.
Copyright The European Southern Observatory (ESO)