Each spherical cloud was obtained from the traditional Monte Carlo scheme:
three normalized random sequences
![]() are transformed
to spherical coordinates
are transformed
to spherical coordinates
![]() according to
the known one-particle distribution function,
or to the density law
according to
the known one-particle distribution function,
or to the density law ![]() .
Regarding the spherical symmetry, the angular coordinates do not
dependent on the radial coordinate.
Thus, we had the radial position calculated from:
.
Regarding the spherical symmetry, the angular coordinates do not
dependent on the radial coordinate.
Thus, we had the radial position calculated from:
The angular coordinates, ![]() and
and ![]() ,
are respectively given by
,
are respectively given by
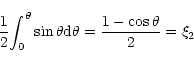 |
(D2) |
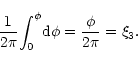 |
(D3) |
Copyright The European Southern Observatory (ESO)