3 The computer experiment: Dissipative collisions of dark molecular clouds

Each collision simulation corresponded to a different impact parameter to verify how this influence on the cloud fragmentation and on the final aspect of the collision remnants. The chosen impact parameters were, b=0(head-on collision), 25% off-center (b=5 pc), 50% off-center (b=10 pc), respectively.

3.1 Physical parameters

The chosen physical scales for length and time were [l]=1 pc, and [t]=1 Myr, respectively, so that velocity unit is approximately 1 km s^-1; the gravity constant was set G=1  [m]^-1[l]³[t]^-2for which the calculated mass unit is [m]=222.25  $M_{\hbox{$\odot$ }}$. Consequently, the derived physical scales for energy, power and density are $[e]=4.230\ {10^{45}}$ erg, $[\dot{e}]=1.340\ {10^{38}}$ erg s^-1, and $[\rho]=1.505\ {10^{-20}}$ g cm^-3 $=9.065\ {10^{3}}$ H cm^-3, respectively.

3.2 Initial conditions

Each spherical cloud was arranged by Monte Carlo so that 4096 particles was distributed according to a given density law, as described in Appendix D. We adopted the 1/r-profile since this is an intermediate stage between homogeneous and isothermal spherical systems according to the empirical relation given by Larson (1981):

$$\rho(r)={M\over 2\pi R_{\rm c}^2}r^{-1},$$ (34)

where the cut-off radius, $R_{\rm c}$, is 10 [l]=10 pc and the total mass M=10 [m]=2222.5 $M_{\hbox{$\odot$ }}$.

All particles were initially at rest relatively to the mass-center of their respective clouds. Each cloud had its mass-center placed at their respective initial positions; in Cartesian coordinates: $(-10~{\rm pc}, b/2, 0)$ for Cloud 1, and $(10~{\rm pc}, -b/2, 0)$ for Cloud 2. The initial velocity, assigned to each particle per object was, respectively, $(5~{\rm km~s}^{-1}, 0, 0)$ for Cloud 1, and $(-5~{\rm km~s}^{-1}, 0, 0)$ for Cloud 2.

Thermodynamics initial conditions were based on observed data (see, e.g., [Shu et al. 1987] for a review). Both objects were initially isothermal, with temperatures of 20 K being a reasonable temperature for dark molecular clouds. This assumption was necessary since it is rather difficult to setup the cooling-heating balance for a non-homogeneous self-gravitating system, by solving ${\cal L}_{_i}=0$for each particle in Eq. (16) and the equations of hydrostatic equilibrium. This difficulty was merely a consequence of the strongly nonlinear dependence of the cooling function on temperatures and densities. Thus, we could not avoid some transient phenomena such as the collapse of the inner parts due to the higher cooling-efficiency in denser regions, and a slight expansion of the outer parts due to the higher heating-efficiency by cosmic rays in comparison to the low cooling-efficiency in rarefied regions. Moreover, the clouds as a whole were initially collapsing but with a collapse time greater than their free-fall time, which is $\sim{10}$ Myr in order of magnitude. However, the collision effects are in fact much more relevant than such transient events.

Figure 3: Projection of the particle configuration onto the orbital plane in the head-on case after 0.25 Myr from the initialconditions

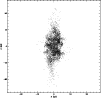Figure 4: Projection of the particle configuration onto the collision plane in the head-on case after 3.5 Myr. The clumped structure of the shock remnants is evident in this figure

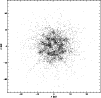Figure 5: The face-on projection of the same configurationillustrated in Fig. 4

Figure 6: Gray-scale density, averaged over a longitudinal slice (midplane) of 0.25 pc in thickness for the head-on collision, after $\sim 1.5$ Myr from the initial conditions. Brighter tones correspond to denser regions, and darker tones correspond to rarefied regions. This figure reveals the thin aspect of the shocking region. The picture's height corresponds to 20 pc. The image is gamma corrected to saturate at the half the maximum density in the slice

3.3 SPH settings

The fluid equations of motion were integrated with the hierarchical leapfrog, with 12 time-bins and setting the root time-step to 0.0078125 Myr. Each experiment took about 4 Myr for head-on and 6 Myr for off-center collisions, respectively.

The experiments ran with variable softening length. The maximum softening length, calculated from Eq. (26), was 0.5 pc, which is approximately the mean interparticle distance for $\sim4000$ particles homogeneously distributed in a sphere of radius 10 pc. The minimum softening length was $\epsilon_{\rm min}=0.05$ pc, which is half the mean interparticle spacing for a hypothetical situation where both clouds were crushed into a dish of about 10 pc in radius, which is a geometrical prediction for the minimum thickness of a shock layer. This adopted value for $\epsilon_{\rm min}$limits Jeans instability to occur only for fragments with sizes greater than $\sim0.05$ pc. In fact, the smallest fragments, with densities as high as 10⁴ cm^-3, were $\sim 0.1$ pc in size, and they stagnated at these scales.

The tolerance parameter was set $\theta=0.25$, which was a good value to guarantee both linear and angular momentum-conservation (e.g., [Barnes & Hut 1989]).

The expected number of the nearest neighbors was determined heuristically regarding a better NNS performance, besides the resolution requirement. We found there is an optimal value for which the NNS is most efficient. One possible explanation for the slow convergence with a small number of neighbors may be that the statistical fluctuation in number increases as smaller is the neighborhood. For instance, if particles are locally distributed far from the Poisson's statistics, a small fluctuation in the search radius may involve a large fluctuation in the number of neighbors found. The explanation for the reduced performance with higher number of neighbors is that the NNS algorithm complexity increases approximately as $O(N_{\rm f}N\log{N})$iterations. We performed some benchmarks with different input parameters, $N_{{\rm f}}$, and we found an optimal choice to set $N_{\rm f}=48\pm2$.

Figure 7: Gray scale temperatures for the head-on collision $\sim 1$ Myr after the initial conditions. Brighter tones correspond to the hotter regions, and darker ones correspond to the colder regions. The darker parts at the center of both clouds have temperatures around 14 K. The temperature of the hot spots is about 200 K. Outer regions have temperature of $\sim 20$ K. The averaging was made within a longitudinal slice of 0.25 pc width passing through the clouds mass center as in Fig. 6

From the SPH theory, the interpolation errors grow asymptotically as O(h²) for the present kernel (e.g., HK89), or equivalently, the interpolation is first-order accurate on h. From this reasoning, we may conclude that SPH linear contrasts are defocused by $\pm(N_{\rm f}/N_{\rm tot})^{1/3}$ from the ideal configuration. However, this factor provides a rather pessimist estimation for shock thickness since the cloud profile was far from homogeneous in all instances of the simulations. In order to globally evaluate how close an interpolation is to an ideal configuration ( $N_{\rm tot}=\infty$), we introduced a resolution-index: $1-(N_{\rm f}/N_{\rm tot})^{1/3}$. For instance, the present choice $N_{\rm f}\approx48$ give us a resolution index of 81.97%, which we considered an acceptable value in comparison to several works in literature. SPH experiments with a number of particles as large as 10⁶ have resolution index better than 95%.

The artificial viscosity input parameters were $\alpha =3$, $\beta =5$, chosen heuristically for numerical stability considerations in adiabatic tests, as discussed in Sect. 2 and we adopted the usual $\eta=0.1$.