For good seeing and good correction, the OTF is well estimated at low frequencies (see examples C1 and C3, and to a less extent, examples A1 and A2). The reconstruction, however, is severely limited by the presence of a residual aberration visible on the first diffraction ring. This aberration which cannot be reproduced by our model can be quite variable. In the case of very bad seeing and very partial correction (examples B), the OTF is always largely underestimated. In this section, we discuss the possible error sources in the PSF reconstruction process and we examine the consequences on the photometric precision we can reach with the ADONIS system.
When computing the covariance matrix of the residual modal coefficients
![]() and when estimating r0 from the variance of the mirror commands, we
assume that the bandwidth of the AO system is higher than
and when estimating r0 from the variance of the mirror commands, we
assume that the bandwidth of the AO system is higher than
![]() ,
the
highest cut-off frequency of the turbulent modes (see Sect. 2.3.1).
As seen in Sect. 2.2.2, the bandwidth of the AO system depends on the corrected
mode via its associated gain. The mean bandwidth of ADONIS is typically about
10 Hz. The highest cut-off frequency of the turbulent modes analyzed by the
system (mirror modes) corresponds roughly to
,
the
highest cut-off frequency of the turbulent modes (see Sect. 2.3.1).
As seen in Sect. 2.2.2, the bandwidth of the AO system depends on the corrected
mode via its associated gain. The mean bandwidth of ADONIS is typically about
10 Hz. The highest cut-off frequency of the turbulent modes analyzed by the
system (mirror modes) corresponds roughly to![]()
 |
(30) |
 |
(31) |
For low bandwidths, the estimated r0 may also be biased leading to a value larger than the true one (see Sect. 3.2) and thus to a Strehl ratio which is larger than the experimental one. However, the Strehl ratios of the estimated PSFs in examples B are smaller than those of the observed PSFs. In addition, when calculating r0 from the high-order mirror modes, we find even smaller values than from the low-order mirror modes. All these results prove that the large reconstruction errors in case B cannot be explained by a too small bandwidth of the AO system. We have no clear explanation for the failure of the reconstruction in case of bad seeing. It may be due to the presence of speckles on the WFS image which induce biases in the calculation of the center of gravity. Simulations may help to verify this hypothesis.
The expression for the long-exposure optical transfer function in Eq. (22)
assumes that the residual phase is a random variable of Gaussian statistics.
As a consequence, the atmospheric residual term in Eq. (22),
given by the product
![]() ,
is real and the corresponding PSF therefore centro-symmetric. The only way to
produce in our model a complex transfer function is through the instrumental
term OTF
,
is real and the corresponding PSF therefore centro-symmetric. The only way to
produce in our model a complex transfer function is through the instrumental
term OTF
![]() ,
via non-common path aberrations which are assumed
to be static.
,
via non-common path aberrations which are assumed
to be static.
Figure 17 shows two series of 10 images of 2 second integration time each and the corresponding long-exposure images (sum of the short-exposure images). A residual aberration is visible on the first diffraction ring. It varies randomly in intensity and direction and hence its origin cannot be due to non-common path aberrations. Furthermore, it is non-stationary and seems to evolve slowly compared to the deformations produced by an atmospheric turbulence. We therefore believe that its origin is due to the presence of a local turbulence, situated e.g. above the primary mirror.
![\begin{figure}\includegraphics[width=8cm]{ds9074f10.eps}\end{figure}](/articles/aas/full/2000/04/ds9074/Timg176.gif) |
Figure 10: The continuous line shows the reconstructed OTF assuming a high bandwidth and the dashed line the reconstructed OTF for a low bandwidth (see text). The dotted line shows the observed OTF |
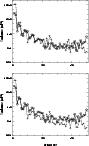 |
Figure 11:
Variance of the mirror commands
|
![\begin{figure}\includegraphics[width=10cm]{ds9074f12.eps}\end{figure}](/articles/aas/full/2000/04/ds9074/Timg186.gif) |
Figure 12:
Estimated values of
|
| PSF |
|
r03-5 | r06-9 | r010-25 | r025-50 |
| C1 (Oct 98) | 17.8 | 17.7 | 15.1 | 11.8 | 8.6 |
| C2 | 16.4 | 16.8 | 13.9 | 12.4 | 8.5 |
| C3 | 20.3 | 18.7 | 16.0 | 14.2 | 11.4 |
| C4 | 18.8 | 19.0 | 15.8 | 12.3 | 8.1 |
| B1 (May 98) | 9.2 | 7.7 | 6.7 | 6.0 | |
| B2 | 7.5 | 6.4 | 5.4 | 5.0 | |
| Dec. 98 | 11.2 | 10.1 | 8.0 | 6.9 | |
Further support for this hypothesis comes from the comparison of the variance
of the mirror commands
![]() with the variances
with the variances
![]() predicted by the theory of Kolmogorov. Figures 11a and b show,
in logarithmic scale,
predicted by the theory of Kolmogorov. Figures 11a and b show,
in logarithmic scale,
![]() (continuous line + circles)
compared to
(continuous line + circles)
compared to
![]() (dashed lines + crosses)
as a function of the mode number i, for r0=14 cm and r0= 19cm, respectively. In the first case, there is a good agreement between both
variances for the modes 11 to 20, while in the second case the agreement is
good for the modes 3 to 5. Note that there is an important deviation from the
theory for the mode 10 and for several higher modes (>25). In Table 3,
we present the values of r0 obtained when fitting the turbulent variance
to the mirror variance on different groups of modes: 3 to 5 (
r03-5),
6 to 9 (
r06-9), 10 to 25 (
r010-25) and 26 to 50 (
r026-50).
The calculated r0 decrease with the degree of the modes.
(dashed lines + crosses)
as a function of the mode number i, for r0=14 cm and r0= 19cm, respectively. In the first case, there is a good agreement between both
variances for the modes 11 to 20, while in the second case the agreement is
good for the modes 3 to 5. Note that there is an important deviation from the
theory for the mode 10 and for several higher modes (>25). In Table 3,
we present the values of r0 obtained when fitting the turbulent variance
to the mirror variance on different groups of modes: 3 to 5 (
r03-5),
6 to 9 (
r06-9), 10 to 25 (
r010-25) and 26 to 50 (
r026-50).
The calculated r0 decrease with the degree of the modes.
This trend cannot be explained by the small bandwidth of the AO system, because we would observe the opposite effect, i.e. an increasing r0 with the mode number (see Sect. 3.2). It can neither be explained by the effect of the outer turbulence scale L0. Indeed, r0 estimated from the variance of the angle-of-arrival, taking into account L0, coincides with r0 estimated from the variance of the mirror modes 3 to 5, but not taking into account L0 (see Sect. 3.2 and Table 3). In addition, the influence of L0 decreases as the mode number increases.
On the other hand, the observed trend of the calculated r0 to decrease
with the mode number, can well be explained by the presence of a local turbulence.
r03-5 being consistent with other independent estimations, we assume
that only the modes superior to 5 are affected by the local turbulence and that
its contribution
![]() to the variance is independent of the
mode:
to the variance is independent of the
mode:
![\begin{figure}\includegraphics[width=10cm]{ds9074f16.eps}\end{figure}](/articles/aas/full/2000/04/ds9074/Timg196.gif) |
Figure 14:
Variance of the local turbulence
|
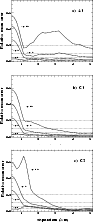 |
Figure 16: Mean relative error on the flux ratio versus the separation of the sources for flux ratios 1, 2, 4 and 10, for a) example A1, for b) example C1 and for c) example C3 |
To have a better insight into the physical properties of this local turbulence,
we calculate the temporal spectral densities of the turbulent modes. They are
shown in Figs. 13a-c. Figure 13a presents
the average power spectrum for the first two modes (tip/tilt). At very low frequencies,
it is proportional to
![]() as predicted from the Kolmogorov model
and the Taylor hypothesis (Conan et al. 1995). Figures 13b
and c show the average power spectrum for the modes 3 to 5 (defocalisation and
astigmatism) and the average power spectrum for the modes 6 to 9 (coma and triangular
coma), respectively. In both figures, the dashed lines represent the predicted
mean spectra, when assuming a frozen Kolmogorov turbulence and a wind speed
of typically 12 m/s (Conan et al. 1995). This theoretical spectra are constant
at low frequencies and decrease as
as predicted from the Kolmogorov model
and the Taylor hypothesis (Conan et al. 1995). Figures 13b
and c show the average power spectrum for the modes 3 to 5 (defocalisation and
astigmatism) and the average power spectrum for the modes 6 to 9 (coma and triangular
coma), respectively. In both figures, the dashed lines represent the predicted
mean spectra, when assuming a frozen Kolmogorov turbulence and a wind speed
of typically 12 m/s (Conan et al. 1995). This theoretical spectra are constant
at low frequencies and decrease as
![]() after a cut-off frequency
of about 3 to 4 Hz. The two observed spectra clearly show the presence of a
turbulent component (grey area) with a cut-off frequency of about 0.5Hz which
cannot be of atmospheric origin. We observe this component for the spectra of
all modes superior to 2. It proves the existence of a local turbulence, probably
located above the primary mirror.
after a cut-off frequency
of about 3 to 4 Hz. The two observed spectra clearly show the presence of a
turbulent component (grey area) with a cut-off frequency of about 0.5Hz which
cannot be of atmospheric origin. We observe this component for the spectra of
all modes superior to 2. It proves the existence of a local turbulence, probably
located above the primary mirror.
From the temporal spectra, we can estimate the contribution of the local turbulence
to the variance of the mirror modes. Figure 14 shows this
contribution and that of the atmospheric turbulence for r0=19 cm.
In this case, i.e. good seeing, they are comparable at high order modes. The
total contribution of the local turbulence to the mirror modes is found to be
about
![]() ,
in very good agreement with the value derived from the
r0 analysis (
,
in very good agreement with the value derived from the
r0 analysis (
![]() ). Note that: i) for the modes 3 to 5,
the force of the local turbulence is much lower than that of the atmospheric
turbulence, and ii) for the modes superior to 5, to a first approximation, it
is constant. This validates a posteriori the hypotheses done in Eq. (32).
Figure 15 shows the variance of the mirror commands
). Note that: i) for the modes 3 to 5,
the force of the local turbulence is much lower than that of the atmospheric
turbulence, and ii) for the modes superior to 5, to a first approximation, it
is constant. This validates a posteriori the hypotheses done in Eq. (32).
Figure 15 shows the variance of the mirror commands
![]() (continuous line + circles) and
(continuous line + circles) and
![]() (
(
![]() is negligible in the present case), the sum of the
variances of the atmospheric and the local turbulence (dashed line + crosses).
Clearly,
is negligible in the present case), the sum of the
variances of the atmospheric and the local turbulence (dashed line + crosses).
Clearly,
![]() is well fitted when taking into account
the term
is well fitted when taking into account
the term
![]() ,
in particular the mode number 10 is much
better reproduced (compare also with Fig. 11).
,
in particular the mode number 10 is much
better reproduced (compare also with Fig. 11).
We have seen that the residual low-order aberration not reproduced by the reconstruction
model can be very variable (examples A) or quite stable (examples C). In this
section, we interpret the residual aberration in the corrected image, at least
its variable part, as the effect of a local turbulence. Why does the system
not correct this low-order aberration efficiently, since the cut-off frequency
is found to be much lower than the correction bandwidth? We have no definite
answer to this question. However, the problem may be due to the influence of
the local turbulence on the remaining error, i.e. the contribution of the high-frequency
phase
![]() to the residual phase. Indeed, the remaining error
is always present, and its relative contribution to the residual phase becomes
even more important, and hence more visible, when the correction is very good,
i.e. when the WFS noise is very small.
to the residual phase. Indeed, the remaining error
is always present, and its relative contribution to the residual phase becomes
even more important, and hence more visible, when the correction is very good,
i.e. when the WFS noise is very small.
We conclude that the residual aberration visible on the first diffraction ring is not necessarily a consequence of a bad low-order correction of the local turbulence, but can be due to the presence of a remaining error highly affected by the local turbulence. It is worth noting that the phenomenon of a variable residual aberration seems not to be restricted to the ADONIS system. Apparently (from private communications), it has also been occasionally observed on the PUEO system (curvature sensor), but with a fainter magnitude.
In this section, we investigate the photometric precision we can expect when
deconvolving science exposures with the reconstructed PSF. For simplicity, we
simulate the image of a binary system by convolving two point sources, having
flux ratios of 1, 2, 4 and 10, with an observed PSF. We consider 8 equidistant
position angles, and we vary the separation between the two sources from 0.6
to 5
![]() .
Then, we deconvolve each image with the reconstructed
PSF using the Lucy-Richardson algorithm. Since the two sources are well separated
after deconvolution, we calculate the flux by integrating within an appropriated
box centered on each source. Figures 16a-c show the relative
error on the calculated flux ratio, averaged over all directions, versus the
separation of the sources, for example A1 for which we could not calibrate the
residual aberration and for examples C1 and C3 for which the residual aberration
was calibrated.
.
Then, we deconvolve each image with the reconstructed
PSF using the Lucy-Richardson algorithm. Since the two sources are well separated
after deconvolution, we calculate the flux by integrating within an appropriated
box centered on each source. Figures 16a-c show the relative
error on the calculated flux ratio, averaged over all directions, versus the
separation of the sources, for example A1 for which we could not calibrate the
residual aberration and for examples C1 and C3 for which the residual aberration
was calibrated.
Without this calibration the error on the calculated flux ratio is quite large at the location of the first diffraction ring (40% for flux ratios of 10 and 10% for flux ratios of 4) and remains important even at large distances (5-15%). When the residual aberration can be calibrated, the error is smaller. For flux ratios larger than 4, it is of the order of 3% at large distances, but it increases to about 5-10% at the location of the first diffraction ring which indicates that the residual aberration has slightly varied from one long exposure image to another. For flux ratios between 1 and 2, the error is less than 3% at all distances.
The error on the flux ratio depends on our exact knowledge of the object's PSF at the time of its acquisition. When reconstructing the PSF from the AO data, this knowledge seems to be essentially limited, at least under good seeing conditions, by the variations of the residual aberration visible on the first diffraction ring. When using an experimental PSF, this knowledge is also limited by the degree of stationarity of the atmospheric turbulence. In order to compare these two approaches, we deconvolve the binary images (simulated with the observed PSF A1) with the observed PSF A2. The errors on the flux ratios are the same than those obtained with the reconstructed PSF. However, the PSF A1 and A2 were obtained on the same star, which is never the case for real observations, and have (by chance?) similar Strehl ratios. Rigaut & Sarazin (1998) predict an uncertainty of 20% on the Strehl ratio, when using only one PSF calibration. In order to obtain an uncertainty of 2% on the Strehl ratio, one has to do about 100 round trips between the PSF and the science object acquisition. This clearly shows the importance of PSF reconstruction from AO data obtained simultaneously to the object image which allows to optimize telescope time and to reach higher photometric precisions. The Strehl ratio is not a sufficient criteria to describe the quality of the PSF as it is well demonstrated by examples A1 and A2 which have essentially the same Strehl ratio, but differ considerably on the first diffraction ring.
Copyright The European Southern Observatory (ESO)