

Up: Characterization of adaptive optics
2 Theoretical estimation of the PSF angular
dependence
Let
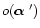 be the object of interest. For wide FOV, the AO corrected
image is given by:
be the object of interest. For wide FOV, the AO corrected
image is given by:
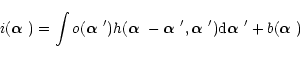 |
(1) |
where
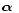 is the angle in the FOV,
is the angle in the FOV,
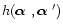 the space
variant long exposure PSF and b an additive zero mean noise.
the space
variant long exposure PSF and b an additive zero mean noise.
Note that, within the isoplanatic patch, Eq. (1)
becomes a convolution between the object and the PSF. In order to well estimate the object
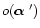 an accurate
knowledge of the PSF
an accurate
knowledge of the PSF
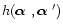 in the whole FOV, is needed.
in the whole FOV, is needed.
The computation of the PSF requires the use of the
residual phase second order statistics. The long exposure Optical Transfer
Function (OTF) (Fourier transform of the PSF) is given by:
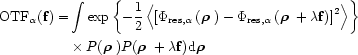 |
(2) |
where
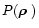 is the telescope pupil function,
is the telescope pupil function,
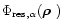 the residual phase in the pupil after AO correction and
the residual phase in the pupil after AO correction and
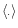 denotes
the expectation over turbulence realizations. The stationarity of the
turbulent phase on the telescope pupil is well known. Conan
Conan-t-94 and Véran Veran-97a have shown
that the AO corrected phase is still quasi-stationary. Then, with this assumption, the OTF expression becomes:
denotes
the expectation over turbulence realizations. The stationarity of the
turbulent phase on the telescope pupil is well known. Conan
Conan-t-94 and Véran Veran-97a have shown
that the AO corrected phase is still quasi-stationary. Then, with this assumption, the OTF expression becomes:
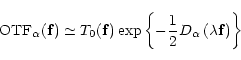 |
(3) |
where
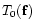 is the telescope transfer function without atmospheric
turbulence, and with
is the telescope transfer function without atmospheric
turbulence, and with
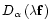 the spatially
average residual phase
structure function:
the spatially
average residual phase
structure function:
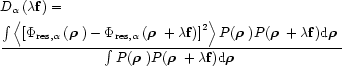 |
(4) |
in a direction 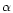 and for a wavelength
and for a wavelength 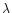 .
Introducing the
on-axis structure function Eq. (4) can be re-written as
.
Introducing the
on-axis structure function Eq. (4) can be re-written as
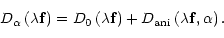 |
(5) |
where
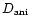 is defined as follows:
is defined as follows:
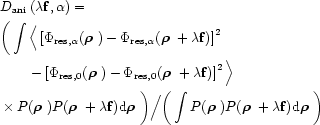 |
(6) |
OTF is the product of OTF0, the OTF on the optical
axis, with a term which can be called "anisoplanatic transfer
function'' (ATF) and reads:
is the product of OTF0, the OTF on the optical
axis, with a term which can be called "anisoplanatic transfer
function'' (ATF) and reads:
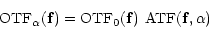 |
(7) |
with
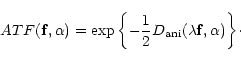 |
(8) |
Note that, on-axis means here: on the wavefront sensor optical axis.
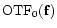 can be estimated using the method proposed by Véran
Veran-97b which is based on real-time data statistics accumulated by the AO control system
during the observation. To obtain a theoretical expression of the ATF,
can be estimated using the method proposed by Véran
Veran-97b which is based on real-time data statistics accumulated by the AO control system
during the observation. To obtain a theoretical expression of the ATF,
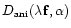 must be computed.
must be computed.
Let us use the modal decomposition of the turbulent phase onto the Zernike
polynomial basis:
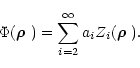 |
(9) |
The properties of turbulence in this particular basis are described by Noll Noll-76.
In a first approximation, the AO correction can be seen as a high-pass filter
which provides a full correction of all the Zernike polynomials up to a given number. With this assumption and for an AO correction
up to the polynomial number i0, we have:
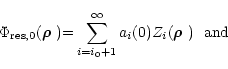 |
(10) |
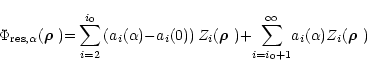 |
(11) |
where ai(0) and
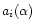 are the Zernike coefficients of
the phase expansion on the optical axis and for a direction
are the Zernike coefficients of
the phase expansion on the optical axis and for a direction 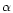 respectively. Using this expansion, a theoretical expression of
respectively. Using this expansion, a theoretical expression of
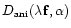 can be obtained:
can be obtained:
![\begin{displaymath}
D_{\rm ani}(\lambda {\bf f},\alpha) =
\sum_{i=1}^{i_0}\sum_{...
...t [C_{i,j}(0) - C_{i,j}(\alpha) \right ]U_{ij}(\lambda{\bf f})
\end{displaymath}](/articles/aas/full/2000/04/ds1812/img38.gif) |
(12) |
where
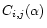 are the angular correlation of the Zernike
coefficients ai and aj,
are the angular correlation of the Zernike
coefficients ai and aj,
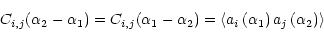 |
(13) |
and Uij are functions defined as:
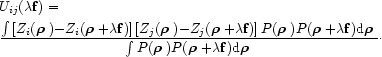 |
(14) |
The angular correlations
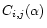 can be theoretically computed
[Chassat1989] assuming that the Cn2 profile is known. Note that a crude estimation of
the Cn2 is enough because of the weak dependency of the angular
correlation of the phase with the atmospheric profile
[Chassat1989,Molodij & Rousset1997]. Nevertheless, a good estimation
of the
can be theoretically computed
[Chassat1989] assuming that the Cn2 profile is known. Note that a crude estimation of
the Cn2 is enough because of the weak dependency of the angular
correlation of the phase with the atmospheric profile
[Chassat1989,Molodij & Rousset1997]. Nevertheless, a good estimation
of the 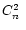 profile can be obtained by a SCIDAR measurement [Fuchs et al.1998], for example.
profile can be obtained by a SCIDAR measurement [Fuchs et al.1998], for example.
Equation (12) is a generalization of the expression given by
Voitsekhovich & Bara Voits-99 who consider the case of a perfect
correction (
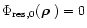 )
on the optical axis. Note that,
because of the difference between the correlations
)
on the optical axis. Note that,
because of the difference between the correlations
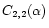 and
and
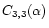 [Chassat1989], Eq. (12) gives an
anisotropic ATF which leads to an elongated PSF [Voitsekhovich & Bara1999,Close et al.1998].
[Chassat1989], Eq. (12) gives an
anisotropic ATF which leads to an elongated PSF [Voitsekhovich & Bara1999,Close et al.1998].
Using Eqs. (7), (8) and
(12), the OTF in the whole field of view can be theoretically
computed, assuming an infinite exposure time.


Up: Characterization of adaptive optics
Copyright The European Southern Observatory (ESO)
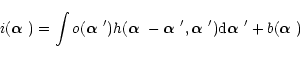
![]() an accurate
knowledge of the PSF
an accurate
knowledge of the PSF
![]() in the whole FOV, is needed.
in the whole FOV, is needed.
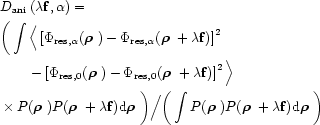
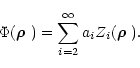
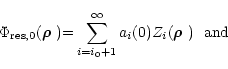
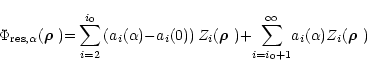
![]() )
on the optical axis. Note that,
because of the difference between the correlations
)
on the optical axis. Note that,
because of the difference between the correlations
![]() and
and
![]() [Chassat1989], Eq. (12) gives an
anisotropic ATF which leads to an elongated PSF [Voitsekhovich & Bara1999,Close et al.1998].
[Chassat1989], Eq. (12) gives an
anisotropic ATF which leads to an elongated PSF [Voitsekhovich & Bara1999,Close et al.1998].