2 Input physics

   
2.1 Initial chemical composition

Stellar models are assumed to be chemically homogeneous when they settle on the zero age main sequence (ZAMS). The helium and metal mass fractions, Y and Z, are chosen according to some fixed Y(Z)relation. In the present models, the values of [Z=0.0004, Y=0.23], [Z=0.001, Y=0.23], [Z=0.004, Y=0.24], and [Z=0.008, Y=0.25], were chosen in order to coincide with the choices previously adopted in Bertelli et al. (1994, and references therein). On the other hand, the set with solar composition was computed with [Z=0.019, Y=0.273], since this value of Y was fixed by the calibration of the solar model (see Sect. 2.6 below). From these 5 pairs of [Z, Y] values, we obtain an helium-to-metal enrichment relation which is $Y\simeq0.23+2.25\,Z$. We then decide to adopt this mean relation for super-solar metallicities. It gives origin to the values of [Z=0.03, Y=0.30] adopted in our set of highest metallicity.

For each value of Z, the fractions of different metals follow a solar-scaled distribution, as compiled by Grevesse & Noels (1993) and adopted in the OPAL opacity tables. The ratio between abundances of different isotopes is according to Anders & Grevesse (1989).

   
2.2 Opacities

The radiative opacities are from the OPAL group (Rogers & Iglesias 1992; Iglesias & Rogers 1993) for temperatures higher than $\log(T/{\rm K})=4.1$, and from Alexander & Ferguson (1994) for $\log(T/{\rm K})<4.0$. In the temperature interval $4.0<\log(T/{\rm K})<4.1$, a linear interpolation between the opacities derived from both sources is adopted. We remind the reader that both opacities sources provide values in good agreement in this temperature interval; the relative differences in opacities are typically lower than 5 percent (see Alexander & Ferguson 1994).

The conductive opacities of electron-degenerate matter are from Hubbard & Lampe (1969). We compared the tracks obtained with this prescription with more recent ones (Salasnich et al., in preparation) which use the Itoh et al. (1983) formulas. No significant differences in the evolutionary features turned out.

   
2.3 Equation of state

The equation of state (EOS) for temperatures higher than 10⁷ K is that of a fully-ionized gas, including electron degeneracy in the way described by Kippenhahn et al. (1965). The effect of Coulomb interactions between the gas particles at high densities is introduced following the prescription by Straniero (1988). The latter was however adapted to the general case of a multiple-component plasma, as described in the Appendix of Girardi et al. (1996a).

For temperatures lower than 10⁷ K, we adopt the detailed "MHD'' EOS of Mihalas et al. (1990, and references therein). The free-energy minimization technique used to derive thermodynamical quantities and derivatives for any input chemical composition, is described in detail by Hummer & Mihalas (1988), Däppen et al. (1988), and Mihalas et al. (1988). In our cases, we explicitly calculated EOS tables for all the Z values of our tracks, using the Mihalas et al. (1990) code. To save computer time, we consider only the four most abundant metal species, i.e. C, N, O, and Ne. For each Z, EOS tables for several closely spaced values of Y were computed, in order to cover the range of surface helium composition found in the evolutionary models before and after the first and second dredge-up events.

Alternatively, we computed some tracks using a much simpler EOS, where the ionization equilibrium and thermo-dynamical quantities were derived by solving a simple set of Saha equations for a H+He mixture (Baker & Kippenhahn 1962). Comparison of these tracks with those obtained with the MHD EOS revealed that no significant differences in effective temperature or luminosity arise for dwarf stars of mass higher than about 0.7 $M_{\odot }$, or for giant stars of any mass. This is so because only dwarf stars of lower mass present the dense and cold envelopes in which the non-ideal effects included in the MHD EOS become important. Moreover, only in the lowest-mass stars the surface temperatures are low enough so that the H₂ molecule is formed, which has dramatic consequences for their internal structures (see e.g. Copeland et al. 1970). Therefore, the use of the MHD EOS is essential for our aim of computing stellar models with masses lower than 0.6 $M_{\odot }$ (see also Girardi et al. 1996b).

   
2.4 Reaction rates and neutrino losses

The network of nuclear reactions we use involves all the important reactions of the pp and CNO chains, and the most important alpha-capture reactions for elements as heavy as Mg (see Bressan et al. 1993 and Maeder 1983 for details).

The reaction rates are from the compilation of Caughlan & Fowler (1988), but for $^{17}{\rm O}({\rm p},\alpha)^{14}{\rm N}$ and $^{17}{\rm O}({\rm p},\gamma)^{18}{\rm F}$, for which we use the more recent determinations by Landré et al. (1990). The uncertain ¹²C( $\alpha,\gamma$)¹⁶O rate was set to 1.7 times the values given by Caughlan & Fowler (1988), as indicated by the study of Weaver & Woosley (1993) on the nucleosynthesis by massive stars. The electron screening factors for all reactions are those from Graboske et al. (1973).

The energy losses by pair, plasma, and bremsstrahlung neutrinos, important in the electron degenerate stellar cores, are taken from Munakata et al. (1985) and Itoh & Kohyama (1983).

   
2.5 Convection

The energy transport in the outer convection zone is described according to the mixing-length theory of Böhm-Vitense (1958). The mixing length parameter $\alpha$ is calibrated by means of the solar model (see Sect. 2.6 below).

The extension of convective boundaries is estimated by means of an algorithm which takes into account overshooting from the borders of both core and envelope convective zones. The formalism is fully described in Bressan et al. (1981) and Alongi et al. (1991). The main parameter describing overshooting is its extent $\Lambda_{\rm c}$ across the border of the convective zone, expressed in units of pressure scale heigth. Importantly, this parameter in the Bressan et al. (1981) formalism is not equivalent to others found in literature. For instance, the overshooting scale defined by $\Lambda_{\rm c}=0.5$ in the Padova formalism roughly corresponds to the 0.25 pressure scale heigth above the convective border, adopted by the Geneva group (Meynet et al. 1994 and references therein) to describe the same physical phenomenum, i.e. $\Lambda^{\rm G}_{\rm c}=0.25$. The non-equivalency of the parameters used to describe convective overshooting by different groups, has been a recurrent source of misunderstanding in the literature.

We adopt the following prescription for the parameter $\Lambda_{\rm c}$ as a function of stellar mass:

• $\Lambda_{\rm c}$ is set to zero for stellar masses $M\le1.0$ $M_{\odot }$, in order to avoid the development of a small central convective zone in the solar model, which would persist up to the present age of 4.6 Gyr;
• For $M\ge1.5$ $M_{\odot }$, we adopt $\Lambda_{\rm c}=0.5$, i.e. a moderate amount of overshoting, which coincides with the values adopted in the previous Bertelli et al. (1994) models;
• In the range 1.0<M<1.5 $M_{\odot }$, we adopt a gradual increase of the overshoot efficiency with mass, i.e. $\Lambda_{\rm c}=M/\mbox{$M_{\odot}$ }- 1.0$. This because the calibration of the overshooting efficiency in this mass range is still very uncertain due to the scarcity of stellar data provided by the oldest intermediate-age and old open clusters. Some works (e.g. Aparicio et al. 1990), however, indicate that this efficiency should be lower than in intermediate-mass stars.

In the stages of core helium burning (CHeB), the value $\Lambda_{\rm c}=0.5$ is used for all stellar masses. This amount of overshooting dramatically reduces the extent of the breathing pulses of convection found in the late phases of CHeB (see Chiosi et al. 1992).

Overshooting at the lower boundary of convective envelopes is also considered. The calibration of the solar model required an envelope overshooting not higher than 0.25 pressure scale heigths. This value of $\Lambda_{\rm e}=0.25$ (see Alongi et al. 1991, for a description of the formalism) was then adopted for the stars with $0.6\le(M/\mbox{$M_{\odot}$ })<2.0$, whereas $\Lambda_{\rm e}=0$ was adopted for M<0.6 $M_{\odot }$. On the other hand, low values of $\Lambda_{\rm e}$ lead to the almost complete suppression of the Cepheid loops in intermediate-mass models (Alongi et al. 1991). Therefore, for M>2.5 $M_{\odot }$ a value of $\Lambda_{\rm e}=0.7$ was assumed as in Bertelli et al. (1994). Finally, for masses between 2.0 and 2.5 $M_{\odot }$, $\Lambda_{\rm e}$ was let to increase gradually from 0.25 to 0.7.

We are well aware that the present prescription for the overshooting parameters seems not to fit on the ideals of simplicity and homogeneity one would like to find in such large sets of evolutionary tracks. However, they represent a pragmatic choice, since the prescriptions previously adopted were not satisfactory in many details.

Figure 1: Evolutionary tracks in the HR diagram, for the models with mass lower than 0.6 $M_{\odot }$, from the ZAMS up to an age of 25 Gyr. For each star, the evolution starts at the full dot and procedes at increasing luminosity, along the continuous lines. For each stellar mass indicated at the left part of the plot, six tracks are presented, for the metallicity values Z=0.0004, 0.001, 0.004, 0.008, 0.019, 0.030 (along the dashed line, from left to right)

   
2.6 Calibration of the solar model

The calibration of the solar model is an essential step in the computation of our evolutionary tracks. Some of the parameters found in the solar model are subsequentely adopted in all the stellar models of our data-base.

We adopt for the Sun the metallicity of Z=0.019, i.e. a value almost identical to the $Z_\odot=0.01886$ favoured by Anders & Grevesse (1989). Several 1 $M_{\odot }$ models, for different values of mixing-length parameter $\alpha$ and helium content $Y_\odot$, are let to evolve up to the age of 4.6 Gyr. From this series of models, we are able to single out the pair of $[\alpha, Y_\odot]$ which allows for a simultaneous match of the present-day solar radius and luminosity, $R_\odot$ and $L_\odot$.

An additional constraint for the solar model comes from the helioseismological determination of the depth of the solar convection zone, of $0.287\pm0.003\;R_{\odot}$ (Christensen-Dalsgaard et al. 1991). It corresponds to a radius of $R_{\rm c}=0.713\;R_{\odot}$ for the lower boundary of the convective envelope. The adoption of an overshooting parameter of $\Lambda_{\rm e}=0.7$, like in Bertelli et al. (1994), would lead to a solar model with too a deep convection zone, namely with $R_{\rm c}=0.680\;R_{\odot}$. This parameter was then reduced to $\Lambda_{\rm e}=0.25$, which allows a reasonable reproduction of the observed value of $R_{\rm c}$.

Our final solar model reproduces well the Sun $R_\odot$, $L_\odot$, and $R_{\rm c}$ values. From this model, we derive the values of $\alpha=1.68$, $Y_\odot=0.273$, and $\Lambda_{\rm e}=0.25$, used in other stellar models as described in the previous subsections.

Figure 2: Evolutionary tracks in the HR diagram, for the composition [Z=0.0004, Y=0.23]. For most tracks of low-mass stars up to the RGB-tip (panel a), and intermediate-mass ones up to the TP-AGB (panel b), the stellar mass (in $M_{\odot }$) is indicated at the initial point of the evolution. For the low-mass tracks from the ZAHB up to the TP-AGB (panels c and d), we indicate the complete range of stellar masses in the upper part of the plots

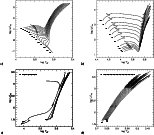Figure 3: The same as Fig. 2, but for [Z=0.030, Y=0.300]