2 The target

In IP XIV we used an eighteen state target comprising all the terms of the 3s²3p, 3s3p², 3s²3d, 3p³ and 3s3p3d electron configurations. These states were expanded in a seventeen configuration basis which included some configurations containing n=4 orbitals. Full details of the composition of that target and the computer codes used to generate it are given in IP XIV. In this paper, we will use the same target as described in IP XIV when dealing with the resonance region, where some scattering channels are closed. In the region of all channels open, above our highest target threshold, we use a simpler target, which contains no n=4orbitals. This was necessary due to the appearance of physically dubious resonances in the open channel region, caused by electron configurations in the target expansion containing n=4 orbitals, but with no associated target states.

   

Table 3: Energies of target levels in Rydberg

Index	Config.	Level	Calculated	Experimental $^\dagger$
1	3s2 3p	2P $^{\rm o}_{1/2}$	0.00000	0.00000
2		2P 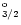$^{\rm o}_{3/2}$	0.16850	0.17179
3	3s 3p2	4P1/2	2.02729	2.05139
4		4P3/2	2.09568	2.12133
5		4P5/2	2.18229	2.20880
6		2D3/2	2.73082	2.72689
7		2D5/2	2.74989	2.74719
8		2S1/2	3.36257	3.32333
9		2P1/2	3.58371	3.54036
10		2P3/2	3.65713	3.61328
11	3s2 3d	2D3/2	4.38676	4.31233
12		2D5/2	4.40889	4.33036
13	3p3	2D 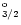$^{\rm o}_{3/2}$	5.25464	5.25239
14		2D 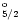$^{\rm o}_{5/2}$	5.28780	5.28747
15		4S 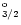$^{\rm o}_{3/2}$	5.37640	5.36738
16	3s 3p 3d	4F 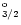$^{\rm o}_{3/2}$	5.87685
17	3p3	2P $^{\rm o}_{1/2}$	5.88362	5.85197
18		2P 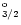$^{\rm o}_{3/2}$	5.91009	a5.88152
19	3s 3p 3d	4F 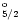$^{\rm o}_{5/2}$	5.91332	5.88668
20		4F 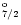$^{\rm o}_{7/2}$	5.96590	5.94097
21		4F 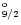$^{\rm o}_{9/2}$	6.03878	6.01676
22		4P 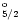$^{\rm o}_{5/2}$	6.33538	6.29051
23		4D 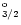$^{\rm o}_{3/2}$	6.35618	6.31200
24		4D $^{\rm o}_{1/2}$	6.37066	6.32573
25		4D 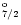$^{\rm o}_{7/2}$	6.45619	6.40979
26		4P $^{\rm o}_{1/2}$	6.44598	6.41304
27		4D 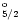$^{\rm o}_{5/2}$	6.45759	6.41636
28		4P 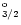$^{\rm o}_{3/2}$	6.45342	6.41723
29		2D 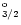$^{\rm o}_{3/2}$	6.59249	6.53556
30		2D 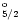$^{\rm o}_{5/2}$	6.59785	6.54163
31		2F 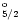$^{\rm o}_{5/2}$	6.88292	6.78862
32		2F 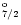$^{\rm o}_{7/2}$	7.01333	6.92394
33		2P 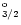$^{\rm o}_{3/2}$	7.46965	7.35496
34		2P $^{\rm o}_{1/2}$	7.54320	7.42797
35		2F 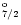$^{\rm o}_{7/2}$	7.57352	7.45046
36		2F 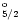$^{\rm o}_{5/2}$	7.59829	7.47787
37		2P $^{\rm o}_{1/2}$	7.79103	7.65002
38		2D 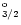$^{\rm o}_{3/2}$	7.80163	7.66171
39		2P 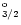$^{\rm o}_{3/2}$	7.82900	7.68796
40		2D 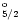$^{\rm o}_{5/2}$	7.83024	7.69544
$^\dagger$ Churilov & Levashov (1993).
a Redfors & Litzén (1989).

The simpler target basis consists of the nine electron configurations of the n=3 complex and, as in IP XIV, the target radial wavefunctions were calculated with the general purpose atomic structure code SUPERSTRUCTURE (Eissner et al. 1974; Nussbaumer & Storey 1978). The scaling parameters for the statistical model potentials for the six orbitals 1s to 3d inclusive are 1.40465, 1.10939, 1.05182, 1.11193, 1.08085, 1.08479. As in IP XIV, the calculation of the target wavefunctions is carried out in LS-coupling, but with the one-body mass and Darwin relativistic energy shifts included. Incorporating these shifts leads to better agreement between the calculated and the experimental energies, without the greatly increased computational cost of carrying out the scattering calculation including fine-structure interactions. In Table 1, we compare the calculated term energies from this calculation (Basis 1) with experiment and with the larger target described in IP XIV (Basis 2). In Table 2, we give gf values for the strongest allowed transitions from the ground state obtained with Basis 1 and Basis 2 and from the much larger "extended basis" described in detail in IP XIV (Basis 3), which we use as a benchmark for the accuracy of the other calculations. The largest difference in gf between Bases 1 and 3 is 3.8%, while the average difference is 1.8%. In the region of all channels open, where we use a target from Basis 1, the collision strengths for the strong allowed transitions are increasingly dominated by contributions from high partial waves whose contribution is directly proportional to the oscillator strength in the transition.

  

 

Table 4: Transition probabilities (A_ji, units s^-1) calculated with the Basis 3 target. The indices (j, i) correspond to the levels as shown in Table 3

j	i	Aji	j	i	Aji	j	i	Aji	j	i	Aji	j	i	Aji
2	1	6.023(+01)	15	3	6.247(+09)	20	5	2.939(+08)	29	6	3.054(+10)	34	10	3.954(+09)
3	1	2.671(+07)	15	4	1.184(+10)	20	7	1.058(+06)	29	7	2.751(+09)	34	11	2.796(+08)
3	2	9.889(+06)	15	5	1.597(+10)	20	12	6.247(+06)	29	8	3.493(+08)	35	5	3.234(+08)
4	1	5.662(+05)	15	6	1.092(+08)	21	5	1.599(+01)	29	9	9.248(+08)	35	7	2.811(+10)
4	2	6.218(+06)	15	10	6.445(+07)	21	7	2.683(+01)	29	10	4.386(+08)	35	12	2.223(+10)
5	2	2.649(+07)	16	3	1.527(+07)	21	12	2.652(-01)	29	11	4.071(+08)	36	6	2.721(+10)
6	1	2.382(+09)	16	4	1.375(+08)	22	4	2.584(+10)	30	4	5.057(+08)	36	7	1.503(+09)
6	2	7.321(+07)	16	6	4.510(+07)	22	5	2.374(+09)	30	5	1.028(+08)	36	10	3.756(+08)
7	2	1.912(+09)	16	7	4.081(+08)	22	6	4.904(+07)	30	6	3.833(+09)	36	11	2.259(+10)
8	1	1.777(+10)	16	8	5.542(+07)	22	7	1.082(+09)	30	7	2.901(+10)	36	12	7.914(+08)
8	2	1.147(+09)	16	9	1.127(+06)	22	10	3.726(+07)	30	10	8.445(+08)	37	8	1.565(+10)
9	1	1.326(+10)	16	10	5.636(+07)	22	12	2.998(+07)	30	11	1.249(+08)	37	9	9.055(+09)
9	2	2.103(+10)	16	11	3.236(+06)	23	3	2.810(+10)	30	12	3.205(+08)	37	10	1.073(+10)
10	1	7.598(+09)	17	3	1.688(+07)	23	4	6.613(+09)	31	4	7.362(+07)	37	11	2.746(+10)
10	2	3.291(+10)	17	4	2.481(+07)	23	5	7.461(+08)	31	5	3.631(+07)	38	7	2.781(+08)
11	1	3.557(+10)	17	6	1.207(+10)	23	6	5.036(+08)	31	6	1.277(+10)	38	8	8.165(+07)
11	2	8.002(+09)	17	8	9.183(+07)	24	3	4.042(+10)	31	7	2.752(+09)	38	9	4.517(+10)
12	2	3.969(+10)	17	9	3.222(+09)	24	4	9.557(+08)	31	11	1.316(+09)	38	10	1.625(+08)
13	3	2.747(+08)	17	10	6.777(+08)	25	5	4.042(+10)	31	12	3.337(+08)	38	11	4.520(+09)
13	4	2.248(+08)	18	3	2.212(+08)	25	7	3.258(+08)	32	5	4.364(+08)	38	12	1.755(+10)
13	5	7.371(+08)	18	4	4.142(+08)	26	4	2.791(+10)	32	7	1.615(+10)	39	6	3.357(+08)
13	6	2.089(+09)	18	5	2.020(+08)	26	6	4.287(+07)	32	12	1.949(+09)	39	7	1.289(+08)
13	7	9.032(+08)	18	6	1.278(+09)	27	4	9.820(+09)	33	3	2.866(+08)	39	8	6.130(+09)
13	8	3.796(+08)	18	7	9.081(+09)	27	5	2.724(+10)	33	8	4.030(+10)	39	9	3.011(+09)
13	9	4.759(+08)	18	8	1.692(+09)	27	6	1.106(+08)	33	9	3.407(+08)	39	10	3.256(+10)
13	10	2.417(+07)	18	10	2.562(+09)	27	7	7.155(+07)	33	10	9.691(+09)	39	11	1.651(+10)
13	11	6.511(+06)	19	4	1.598(+08)	28	4	1.979(+10)	33	11	6.513(+08)	39	12	1.001(+10)
14	5	9.498(+07)	19	5	8.858(+07)	28	5	1.212(+10)	33	12	3.253(+08)	40	10	5.810(+10)
14	6	3.072(+08)	19	6	1.388(+06)	28	6	1.012(+08)	34	3	1.279(+08)	40	11	3.304(+08)
14	7	2.947(+09)	19	7	8.428(+07)	28	7	9.150(+07)	34	6	2.538(+08)	40	12	1.915(+10)
14	10	6.666(+08)	19	10	5.646(+05)	29	3	4.833(+08)	34	8	1.436(+10)
14	12	7.708(+06)	19	11	4.990(+06)	29	4	5.457(+07)	34	9	2.690(+10)

In Table 3 we give a list of the forty levels arising from the eighteen target terms, together with their calculated and experimental energies where these are known (Churilov & Levashov 1993; Redfors & Litzén 1989). The calculations were made in Basis 2 and include the one- and two-body fine-structure interactions described by Eissner et al. (1974). The levels are given in the experimental energy order. Table 3 serves as a key to the levels for use in later tabulations of collision strengths and effective collision strengths. In Sect. 6 we shall calculate the emissivities of the transitions arising from these levels. For this purpose we will use transition probabilities computed using our most extended basis, Basis 3. The results are in Table 4, where we give the Einstein A-values for the strongest transitions from each upper level. A transition is excluded if the A-value is less than 0.1 percent of the total A-value from that particular upper state. The calculation of the A-values includes empirical corrections to the Hamiltonian of the system as described by Zeippen et al. (1977), whose purpose is to bring the computed level energies into agreement with the experimental values.