

Up: Atomic data from the
2 The target
In IP XIV we used an eighteen state target comprising all the terms
of the 3s23p, 3s3p2, 3s23d, 3p3 and 3s3p3d electron
configurations. These states were expanded in a seventeen configuration
basis which included some configurations containing n=4 orbitals. Full
details of the composition of that target and the computer codes used to
generate it are given in IP XIV. In this paper, we will use the same target as
described in IP XIV when dealing with the resonance region, where some
scattering channels are closed. In the region of all channels open, above
our highest target threshold, we use a simpler target, which contains no n=4orbitals. This was necessary due to the appearance of physically dubious
resonances in the open channel region, caused by electron configurations in
the target expansion containing n=4 orbitals, but with no associated target
states.
Table 3:
Energies of target levels in Rydberg
| Index |
Config. |
Level |
Calculated |
Experimental
 |
| 1 |
3s2 3p |
2P
 |
0.00000 |
0.00000 |
| 2 |
|
2P
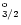 |
0.16850 |
0.17179 |
| 3 |
3s 3p2 |
4P1/2 |
2.02729 |
2.05139 |
| 4 |
|
4P3/2 |
2.09568 |
2.12133 |
| 5 |
|
4P5/2 |
2.18229 |
2.20880 |
| 6 |
|
2D3/2 |
2.73082 |
2.72689 |
| 7 |
|
2D5/2 |
2.74989 |
2.74719 |
| 8 |
|
2S1/2 |
3.36257 |
3.32333 |
| 9 |
|
2P1/2 |
3.58371 |
3.54036 |
| 10 |
|
2P3/2 |
3.65713 |
3.61328 |
| 11 |
3s2 3d |
2D3/2 |
4.38676 |
4.31233 |
| 12 |
|
2D5/2 |
4.40889 |
4.33036 |
| 13 |
3p3 |
2D
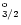 |
5.25464 |
5.25239 |
| 14 |
|
2D
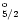 |
5.28780 |
5.28747 |
| 15 |
|
4S
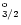 |
5.37640 |
5.36738 |
| 16 |
3s 3p 3d |
4F
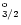 |
5.87685 |
|
| 17 |
3p3 |
2P
 |
5.88362 |
5.85197 |
| 18 |
|
2P
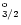 |
5.91009 |
a5.88152 |
| 19 |
3s 3p 3d |
4F
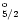 |
5.91332 |
5.88668 |
| 20 |
|
4F
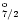 |
5.96590 |
5.94097 |
| 21 |
|
4F
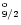 |
6.03878 |
6.01676 |
| 22 |
|
4P
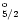 |
6.33538 |
6.29051 |
| 23 |
|
4D
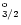 |
6.35618 |
6.31200 |
| 24 |
|
4D
 |
6.37066 |
6.32573 |
| 25 |
|
4D
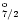 |
6.45619 |
6.40979 |
| 26 |
|
4P
 |
6.44598 |
6.41304 |
| 27 |
|
4D
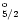 |
6.45759 |
6.41636 |
| 28 |
|
4P
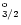 |
6.45342 |
6.41723 |
| 29 |
|
2D
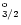 |
6.59249 |
6.53556 |
| 30 |
|
2D
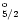 |
6.59785 |
6.54163 |
| 31 |
|
2F
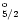 |
6.88292 |
6.78862 |
| 32 |
|
2F
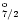 |
7.01333 |
6.92394 |
| 33 |
|
2P
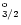 |
7.46965 |
7.35496 |
| 34 |
|
2P
 |
7.54320 |
7.42797 |
| 35 |
|
2F
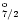 |
7.57352 |
7.45046 |
| 36 |
|
2F
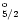 |
7.59829 |
7.47787 |
| 37 |
|
2P
 |
7.79103 |
7.65002 |
| 38 |
|
2D
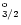 |
7.80163 |
7.66171 |
| 39 |
|
2P
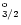 |
7.82900 |
7.68796 |
| 40 |
|
2D
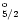 |
7.83024 |
7.69544 |
 Churilov & Levashov (1993).
Churilov & Levashov (1993). |
| a Redfors & Litzén (1989). |
The simpler target basis consists of the nine electron configurations of the
n=3 complex and, as in IP XIV, the target radial wavefunctions were
calculated with the general purpose atomic structure code SUPERSTRUCTURE
(Eissner et al. 1974; Nussbaumer & Storey 1978). The scaling parameters for
the statistical model potentials for the six orbitals 1s to 3d inclusive are
1.40465, 1.10939, 1.05182, 1.11193, 1.08085, 1.08479. As in IP XIV, the
calculation of the target wavefunctions is carried out in LS-coupling, but
with the one-body mass and Darwin relativistic energy shifts included.
Incorporating these shifts leads to better agreement between the calculated
and the experimental energies, without the greatly increased computational
cost of carrying out the scattering calculation including fine-structure
interactions. In Table 1, we compare the calculated
term energies from this calculation (Basis 1) with experiment and with the
larger target described in IP XIV (Basis 2). In
Table 2, we give gf values for the strongest allowed
transitions from the ground state obtained with Basis 1 and Basis 2 and from
the much larger "extended basis" described in detail in IP XIV (Basis 3),
which we use as a benchmark for the accuracy of the other calculations. The
largest difference in gf between Bases 1 and 3 is 3.8%, while the average
difference is 1.8%. In the region of all channels open, where we use a
target from Basis 1, the collision strengths for the strong allowed
transitions are increasingly dominated by contributions from high partial
waves whose contribution is directly proportional to the oscillator strength
in the transition.
Table 4:
Transition probabilities (Aji, units s-1) calculated with
the Basis 3 target. The indices (j, i) correspond to the
levels as shown in Table 3
| j |
i |
Aji |
j |
i |
Aji |
j |
i |
Aji |
j |
i |
Aji |
j |
i |
Aji |
| 2 |
1 |
6.023(+01) |
15 |
3 |
6.247(+09) |
20 |
5 |
2.939(+08) |
29 |
6 |
3.054(+10) |
34 |
10 |
3.954(+09) |
| 3 |
1 |
2.671(+07) |
15 |
4 |
1.184(+10) |
20 |
7 |
1.058(+06) |
29 |
7 |
2.751(+09) |
34 |
11 |
2.796(+08) |
| 3 |
2 |
9.889(+06) |
15 |
5 |
1.597(+10) |
20 |
12 |
6.247(+06) |
29 |
8 |
3.493(+08) |
35 |
5 |
3.234(+08) |
| 4 |
1 |
5.662(+05) |
15 |
6 |
1.092(+08) |
21 |
5 |
1.599(+01) |
29 |
9 |
9.248(+08) |
35 |
7 |
2.811(+10) |
| 4 |
2 |
6.218(+06) |
15 |
10 |
6.445(+07) |
21 |
7 |
2.683(+01) |
29 |
10 |
4.386(+08) |
35 |
12 |
2.223(+10) |
| 5 |
2 |
2.649(+07) |
16 |
3 |
1.527(+07) |
21 |
12 |
2.652(-01) |
29 |
11 |
4.071(+08) |
36 |
6 |
2.721(+10) |
| 6 |
1 |
2.382(+09) |
16 |
4 |
1.375(+08) |
22 |
4 |
2.584(+10) |
30 |
4 |
5.057(+08) |
36 |
7 |
1.503(+09) |
| 6 |
2 |
7.321(+07) |
16 |
6 |
4.510(+07) |
22 |
5 |
2.374(+09) |
30 |
5 |
1.028(+08) |
36 |
10 |
3.756(+08) |
| 7 |
2 |
1.912(+09) |
16 |
7 |
4.081(+08) |
22 |
6 |
4.904(+07) |
30 |
6 |
3.833(+09) |
36 |
11 |
2.259(+10) |
| 8 |
1 |
1.777(+10) |
16 |
8 |
5.542(+07) |
22 |
7 |
1.082(+09) |
30 |
7 |
2.901(+10) |
36 |
12 |
7.914(+08) |
| 8 |
2 |
1.147(+09) |
16 |
9 |
1.127(+06) |
22 |
10 |
3.726(+07) |
30 |
10 |
8.445(+08) |
37 |
8 |
1.565(+10) |
| 9 |
1 |
1.326(+10) |
16 |
10 |
5.636(+07) |
22 |
12 |
2.998(+07) |
30 |
11 |
1.249(+08) |
37 |
9 |
9.055(+09) |
| 9 |
2 |
2.103(+10) |
16 |
11 |
3.236(+06) |
23 |
3 |
2.810(+10) |
30 |
12 |
3.205(+08) |
37 |
10 |
1.073(+10) |
| 10 |
1 |
7.598(+09) |
17 |
3 |
1.688(+07) |
23 |
4 |
6.613(+09) |
31 |
4 |
7.362(+07) |
37 |
11 |
2.746(+10) |
| 10 |
2 |
3.291(+10) |
17 |
4 |
2.481(+07) |
23 |
5 |
7.461(+08) |
31 |
5 |
3.631(+07) |
38 |
7 |
2.781(+08) |
| 11 |
1 |
3.557(+10) |
17 |
6 |
1.207(+10) |
23 |
6 |
5.036(+08) |
31 |
6 |
1.277(+10) |
38 |
8 |
8.165(+07) |
| 11 |
2 |
8.002(+09) |
17 |
8 |
9.183(+07) |
24 |
3 |
4.042(+10) |
31 |
7 |
2.752(+09) |
38 |
9 |
4.517(+10) |
| 12 |
2 |
3.969(+10) |
17 |
9 |
3.222(+09) |
24 |
4 |
9.557(+08) |
31 |
11 |
1.316(+09) |
38 |
10 |
1.625(+08) |
| 13 |
3 |
2.747(+08) |
17 |
10 |
6.777(+08) |
25 |
5 |
4.042(+10) |
31 |
12 |
3.337(+08) |
38 |
11 |
4.520(+09) |
| 13 |
4 |
2.248(+08) |
18 |
3 |
2.212(+08) |
25 |
7 |
3.258(+08) |
32 |
5 |
4.364(+08) |
38 |
12 |
1.755(+10) |
| 13 |
5 |
7.371(+08) |
18 |
4 |
4.142(+08) |
26 |
4 |
2.791(+10) |
32 |
7 |
1.615(+10) |
39 |
6 |
3.357(+08) |
| 13 |
6 |
2.089(+09) |
18 |
5 |
2.020(+08) |
26 |
6 |
4.287(+07) |
32 |
12 |
1.949(+09) |
39 |
7 |
1.289(+08) |
| 13 |
7 |
9.032(+08) |
18 |
6 |
1.278(+09) |
27 |
4 |
9.820(+09) |
33 |
3 |
2.866(+08) |
39 |
8 |
6.130(+09) |
| 13 |
8 |
3.796(+08) |
18 |
7 |
9.081(+09) |
27 |
5 |
2.724(+10) |
33 |
8 |
4.030(+10) |
39 |
9 |
3.011(+09) |
| 13 |
9 |
4.759(+08) |
18 |
8 |
1.692(+09) |
27 |
6 |
1.106(+08) |
33 |
9 |
3.407(+08) |
39 |
10 |
3.256(+10) |
| 13 |
10 |
2.417(+07) |
18 |
10 |
2.562(+09) |
27 |
7 |
7.155(+07) |
33 |
10 |
9.691(+09) |
39 |
11 |
1.651(+10) |
| 13 |
11 |
6.511(+06) |
19 |
4 |
1.598(+08) |
28 |
4 |
1.979(+10) |
33 |
11 |
6.513(+08) |
39 |
12 |
1.001(+10) |
| 14 |
5 |
9.498(+07) |
19 |
5 |
8.858(+07) |
28 |
5 |
1.212(+10) |
33 |
12 |
3.253(+08) |
40 |
10 |
5.810(+10) |
| 14 |
6 |
3.072(+08) |
19 |
6 |
1.388(+06) |
28 |
6 |
1.012(+08) |
34 |
3 |
1.279(+08) |
40 |
11 |
3.304(+08) |
| 14 |
7 |
2.947(+09) |
19 |
7 |
8.428(+07) |
28 |
7 |
9.150(+07) |
34 |
6 |
2.538(+08) |
40 |
12 |
1.915(+10) |
| 14 |
10 |
6.666(+08) |
19 |
10 |
5.646(+05) |
29 |
3 |
4.833(+08) |
34 |
8 |
1.436(+10) |
|
|
|
| 14 |
12 |
7.708(+06) |
19 |
11 |
4.990(+06) |
29 |
4 |
5.457(+07) |
34 |
9 |
2.690(+10) |
|
|
|
In Table 3 we give a list of the forty
levels arising from the eighteen target terms, together with their
calculated and experimental energies where these are known (Churilov &
Levashov 1993; Redfors & Litzén 1989).
The calculations were made in Basis 2 and include the
one- and two-body fine-structure interactions described by Eissner et al.
(1974). The levels are given in the experimental energy order.
Table 3 serves as a key to the levels for use in
later tabulations of collision strengths and effective collision strengths.
In Sect. 6 we shall calculate the emissivities of the transitions arising
from these levels. For this purpose we will use transition probabilities
computed using our most extended basis, Basis 3. The results are in
Table 4, where we give the Einstein A-values for the
strongest transitions from each upper level. A transition is excluded if the
A-value is less than 0.1 percent of the total A-value from that particular
upper state. The calculation of the A-values includes empirical
corrections to the Hamiltonian of the system as described by Zeippen et al.
(1977), whose purpose is to bring the computed level energies into agreement
with the experimental values.


Up: Atomic data from the
Copyright The European Southern Observatory (ESO)