Appendix A: Angular correlation function amplitude uncertainty

The uncertainty in the amplitude of the angular correlation function of a fiducial radio survey with limiting flux density $S_{\rm lim}$, subtended over a solid angle $\Omega$, is estimated here. To simplify the procedure, the following assumptions are made:

1. the area subtended by the survey has a circular geometry;
2. the angular correlation function of radio sources is a power law of the form $w(\theta)=A_{w}\theta^{-\delta}$, with the index $\delta$ being fixed;
3. the values of $w(\theta )$ at different angular separations are uncorrelated;
4. The uncertainty in $w(\theta )$ follows Poisson statistics (Peebles 1980) and is given by

$$\delta w(\theta) =\sqrt{\frac {1+w(\theta)}{DD}},$$

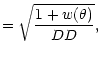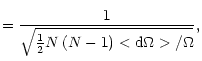$$=\frac {1}{\sqrt{\frac{1}{2}N\,(N-1) <{\rm d}\Omega>/\Omega}},$$ (A1)

where DD is the number of data-data pairs with angular separations $\theta$ and $\theta + {\rm d}\theta$, N is the number of sources above the flux density limit and $<{\rm d}\Omega>$ is the mean value of solid angle subtended by annuli with inner and outer radii $\theta$ and $\theta + {\rm d}\theta$ respectively. The value of $<{\rm d}\Omega>$ is affected by the field boundaries. In the present study, this is estimated by creating simulated catalogues of sources distributed randomly over the area of the survey and calculating the expected number of random points, RR, with separations $\theta$ to $\theta + {\rm d}\theta$. This is given by

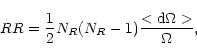$$RR =\frac{1}{2}N_{R}(N_{R}-1)\frac{<{\rm d}\Omega>}{\Omega},$$ (A2)

where N_R is the number of sources in the simulated dataset. The assumption of Poisson errors underestimates the uncertainty in A_w (Bernstein 1994).

The assumptions (iii) and (iv) allow us to use least squares fitting techniques to estimate the uncertainty in A_w

$$\delta A_{w}=\biggl (\sum_{i=\theta_{\rm min}}^{\theta_{\rm... ...ga}}{\delta w(\theta_{i})}\biggr)^{2} \biggr)^{-\frac{1}{2}},$$ (A3)

where $\omega_{\Omega}$ is the integral constraint defined in Sect. 3. The summation is carried out between a minimum ( $\theta_{\rm min}$) and a maximum ( $\theta_{\rm max}$) angular separation within equally separated logarithmic bins of width $\Delta$log $\theta=0.2$($\theta$ in degrees). The former is taken to be 3$^{\prime}$ and the latter is set three times smaller than the radius of the survey, while it cannot be larger than 1$^{\circ }$. This is because in real surveys one needs to minimise the effects of field boundaries when estimating A_w. Additionally, one is interested in the value of A_w on small scales, while for larger scales the angular correlation function may deviate from a power law. For example in the optical wavelengths Maddox et al. (1990a) found a break in $w(\theta )$ at scales $\theta\approx1.5''$.