6 The model

Let us assume that the evolution of clustering of galaxies with redshift is parametrised by $\epsilon$ such that their spatial correlation function is (Phillipps et al. 1978)

$\begin{displaymath} \xi(r,z)=\biggl(\frac{r}{r_0}\biggr) ^{-\gamma}(1+z)^{-(3+\epsilon)}, \end{displaymath}$

(12)

where r is the proper length and r₀ the correlation length for z=0, corresponding to the scale where the clustering becomes non-linear. The clustering evolution parameter has the property that if $\epsilon\geq 0$ the physical length of a typical cluster reduces with time, resulting in a growth of clustering in proper coordinates. Values of $\epsilon<0$ result in reduction in clustering strength with time. The case of $\epsilon\approx -1.2$ corresponds to clusters of fixed size in co-moving coordinates. If the redshift distribution ${\rm d}N/{\rm d}z$ of galaxies is known, then the angular correlation function $w(\theta )$ can be related to $\xi(r)$ by the Limber equation (Limber 1953; Phillipps et al. 1978)

	$\textstyle w(\theta)=Cr_0^{1-\gamma} \theta^{-(\gamma-1)} \int_0^\infty D(z)^{1-\gamma}g(z)^{-1}$
	$\textstyle \times (1+z)^{-(3+\epsilon)} \biggl(\frac{{\rm d}N}{{\rm d}z}\biggr) ^{2}\,{\rm d}z$
	$\textstyle \times \biggl[\int_0^\infty \frac{{\rm d}N}{{\rm d}z}\,{\rm d}z \biggr] ^{-2}.$		(13)

Here, D(z), g(z) and C are defined as

$\begin{displaymath} D(z)=\frac{c}{H_{\rm o}q_{\rm o}^{2}} \frac{q_{\rm o}z+(q_{\rm o}-1)(\sqrt{1+2q_{\rm o}z}-1)}{(1+z)^2}, \end{displaymath}$

(14)

$\begin{displaymath} g(z)=\frac{c}{H_{\rm o}} \frac{1}{(1+z)^{2} \sqrt{1+2q_{\rm o}z}}, \end{displaymath}$

(15)

$\begin{displaymath} C=\sqrt{\pi} \frac{\Gamma((\gamma-1)/2)}{\Gamma(\gamma /2)}. \end{displaymath}$

(16)

It is evident that the exponent $\gamma$ of the spatial correlation function is related to the index $\delta$ of the angular correlation function via the relation $\gamma=\delta+1$ . Unlike optically selected galaxies, the redshift information of the faint radio population is sparse and restricted only to sources with optical counterparts that are relatively bright. Therefore, to predict the amplitudes of the correlation function using Eq. (13) for different input parameters ( $\epsilon$ , r₀, $\gamma$ ), we need to use a model radio luminosity function (RLF) to estimate their redshift distribution. In the present work the evolving radio luminosity functions of Dunlop & Peacock (1990) at 2.7GHz (Model 1) and Rowan-Robinson et al. (1993) at 1.4GHz (Model 2), extrapolated to faint flux densities, are used. Dunlop & Peacock (1990) considered the free form luminosity function of both flat and steep spectrum radio galaxies. Their proposed evolutionary model implies that the radio sources of higher power evolve faster, with the evolution of flat and steep spectrum radio sources being similar. Here we employ their RLF1 model (using their RLF2, RLF3 and RLF4 models give similar results) shifted to 1.4GHz and converted to WHz^-1. The transformation from 2.7GHz to 1.4GHz was carried out assuming a power law spectral index $\alpha$ ( $S_{\nu} \propto \nu ^{-\alpha}$ ) of 0.8 for steep spectrum and 0.0 for flat spectrum radio sources. The redshift distributions at different flux limits for Dunlop & Peacock models are shown in Fig. 8. The median of the redshift distribution for flux limits of 0.1, 0.5 and 1mJy is 0.84, 0.85 and 0.91 respectively.

$\begin{figure} {\psfig{figure=ag8556f8.eps,width=8.8cm,angle=0} } \end{figure}$

Figure 8: Redshift distributions for different flux density cutoffs using the radio luminosity function introduced by Dunlop & Peacock (1990). Dashed line: Steep spectrum radio sources; Dotted line: Flat spectrum radio sources ; Solid line: both populations. The normalisation of the redshift distribution is arbitrary

Rowan-Robinson et al. (1993) divided the radio population into spirals, which they showed to be indistinguishable from the starburst galaxies detected at 60 $\mu$ m by IRAS, and ellipticals. For the former population we employ Saunders et al. (1990) "warm'' IRAS galaxy component luminosity function at 60 $\mu$ m translated to 1.4GHz using the empirical relation derived by Helou et al. (1985). For ellipticals, following Rowan-Robinson et al. (1993), we use Dunlop & Peacock (1990) pure luminosity evolution model RLF6 (parameters from their Table C3). To match the source counts and the redshift distribution of the optically brighter radio sources, pure luminosity evolution for the spiral galaxy component is invoked as described in Rowan-Robinson et al. (1993) and Hopkins et al. (1998). The predicted redshift distributions at different flux density limits are plotted in Fig. 9. The median of the redshift distribution for flux limits of 0.1, 0.5 and 1mJy is 1.34, 1.37 and 1.44 respectively, significantly larger than the median values predicted by the model developed by Dunlop & Peacock (1990). Thus, the correlation amplitudes predicted by this RLF model are lower compared to the previous one, for the same parameters r₀, $\epsilon$ .

$\begin{figure}{\psfig{figure=ag8556f9.eps,width=0.45\textwidth,angle=0} } \end{figure}$

Figure 9: Redshift distributions for different flux density cutoffs using the radio luminosity function described by Rowan-Robinson et al. (1993). Dashed line: Ellipticals; Dotted line: Spirals; Solid line: both populations. The normalization of the redshift distribution is arbitrary

Using Eq. (13) we predict the amplitudes of $w(\theta )$ for different values of $\epsilon$ , r₀, $\gamma$ and for different radio luminosity functions. The value of $\gamma$ is fixed to either 1.8 or 2.1, with the models calculated for each value of $\gamma$ independently. Upper limits for the clustering length r₀ for $\epsilon =-1.2$ , are listed in Table 4. The error estimates of r₀ are calculated from the 3 $\sigma_{\rm Poisson}$ correlation amplitude uncertainties (Table 2).

**Table 4:** Upper limits of the clustering length, for $\epsilon =-1.2$ and for two RLF models. Model 1: Dunlop & Peacock (1990) RLF; model 2: RLF described by Rowan-Robinson et al. (1993). The superscripts are the upper limits to the errors in the r₀ estimates, corresponding to the bootstrap uncertainties of the angular correlation amplitude
	$r_0^{\gamma=(2.1)}$ h^-1Mpc		$r_0^{\gamma=(1.8)}$ h^-1Mpc
S_1.4 (mJy)	model 1	model 2	model 1	model 2
>0.4	4⁺³	5⁺³	6⁺⁶	7⁺⁹
>0.5	7⁺²	9⁺³	9⁺⁶	11⁺⁹
>0.9	8⁺⁴	10⁺⁵	11⁺⁸	13⁺¹⁰
[0.4,0.9]	7⁺⁸	9⁺⁶	9⁺¹²	12⁺¹²

$\begin{figure}{\psfig{figure=ag8556f10.eps,width=0.45\textwidth,angle=0} } \end{figure}$

Figure 10: Predicted amplitude of the angular correlation function at different flux density cutoffs, assuming that the radio population consists of starbursts and elliptical galaxies with different clustering properties Solid line: r₀=5h^-1Mpc for starbursts, r₀=11h^-1Mpc for ellipticals (Model A); Dashed line: r₀ = 11h^-1Mpc for both populations (Model B). The clustering evolution parameter is taken to be 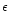$\epsilon$ = -1.2 and $\gamma$ = 1.8 for both populations. Also shown are the estimated amplitudes from this work (filled circles; upper limits) and for sources with $1\le S_{1.4}\le 2$ mJy detected in the FIRST survey

Up: The Phoenix radio survey: