3 Two point correlation function

The two-point angular correlation function, $w(\theta )$, is defined as the joint probability $\delta P$ of finding sources within the solid angle elements $\delta \Omega_{1}$ and $\delta \Omega_{2}$, separated by an angle $\theta$, in the form

$$\delta P= N^{2}\, (1+w(\theta)) \delta \Omega_{1} \delta \Omega_{2},$$ (1)

where N is the mean surface density of galaxies. For a random distribution of sources $w(\theta)=0$. Therefore, the angular correlation function provides a measure of galaxy density excess over that expected for a random distribution. Various methods for estimating $w(\theta )$ have been introduced, as discussed by Infante (1994). In the present study, a source is taken as the "centre'' and the number of pairs within annular rings is counted. To account for the edge effects, Monte Carlo techniques are used by placing random points within the area of the survey. The most commonly used estimators in this procedure have the form

$$w=\frac{DD}{RR} - 1,\; \mathrm {or}$$ (2)

$$w=\frac{DD}{DR} - 1,$$ (3)

where DD and DR are respectively the number of sources and random points computed at separations $\theta$ and $\theta + {\rm d}\theta$ from a given galaxy. Similarly, RR is the number of random points within the angular interval $\theta$ to $\theta + {\rm d}\theta$ from a given random point. Infante (1994) and Hewett (1982) emphasised the importance of correcting for any spurious cross correlation between the random and the galaxy catalogues when using the above estimators, arising partly because of the anisotropic and inhomogeneous galaxy distribution relative to the field boundaries. The corrected form of the estimator is then

$$w=\frac{DD}{DR} - \frac{RD}{RR},$$ (4)

where RD is the number of random-data pairs, taking the random points as centres (Infante 1994). Landy & Szalay (1993, hereafter LS) introduced the estimator

$$w=\frac{DD-2DR+RR}{RR}.$$ (5)

The advantages of this estimator is that it minimises the variance of $w(\theta )$ and also reduces the edge effects from which both the estimators (3) and (4) suffer. Moreover, it has similar properties (Landy & Szalay 1993) to that introduced by Hamilton (1993)

$$w=\frac{DD\, RR}{DR\, DR}-1.$$ (6)

In the present study the correlation function has been calculated using estimators (4), (5) and (6). The results agree within the respective uncertainties. Therefore, only the results from the LS estimator are presented. For a given radio galaxy sample, a total of 100 random catalogues were generated, each having the same number of points as the original data set. The random sets were cross-correlated with the galaxy catalogue, giving an average value for $w(\theta )$ at each angular separation. In producing random sets of points, we take into account variations in sensitivity, which might affect the correlation function estimate. The flux density threshold for detection depends on the local rms noise which varies across the survey area. Since the random fields are expected to have the same sources of bias as the data (i.e. the simulated catalogues must have the same selection effects as the real catalogue), the rms noise map, with a resolution of $\approx$10arcsec, is used to discard simulated points in noisy areas. This is accomplished, to the first approximation, by assigning a flux density to random points using the Windhorst et al. (1985) $\log N-\log S$ distribution, following the method of Cress et al. (1996). If the flux density of the random point is less than 4 times the local rms noise, the point is excluded from the random data set. However, producing random points with a uniform distribution over the observed area does not change our final result.

The uncertainty in w($\theta$) is determined using both Poisson statistics and 50 bootstrap resamples of the data (Ling et al. 1986). For the latter method, simulated data-sets were generated by sampling N points with replacement from the true data-set of N points. The correlation function is then calculated for each of the bootstrap samples, following the same procedure as that with the original data-set. The standard deviation around the mean is then used to estimate the uncertainty in the correlation function.

Although the LS estimator used here is shown to have Poissonian variance for uncorrelated points (Landy & Szalay 1993), it does not necessarily behave this way for correlated data. The bootstrap method is believed to give a more representative estimate of the uncertainty associated with $w(\theta )$. However, Fisher et al. (1994) carried out a detailed study of the biases affecting the bootstrap errors (e.g. cosmic variance, sparse sampling by galaxies of the underlying density distribution) and concluded that overall the bootstrap uncertainties overestimate the true errors. Nevertheless, the bootstrap resampling is a general method for assessing the accuracy of the angular correlation function estimator and it will be used here to calculate the formal errors. The uncertainty associated with $w(\theta )$, estimated by the bootstrap resampling technique, is found to be about three times larger than the Poisson estimate.

  

Table 1: Number of sources in each flux density-limited subsample

Flux density (mJy)	Number of Sources
>0.4	634
>0.5	529
>0.6	454
>0.7	391
>0.9	316
[0.4, 0.9]	318

There is expected be a significant number of physical double sources in a radio survey with the angular resolution of the Phoenix survey ( $\approx8^{\prime\prime}$). In any study of the clustering of radio galaxies via correlation analysis, these should not be considered as two sources since both components are formed in the same galaxy. To identify groups of sources that are likely to be sub-components of a single source we have employed a percolation technique where all sources within a given radius are replaced by a single source at an appropriate "centroid'' (Cress et al. 1996; Magliocchetti et al. 1998). Following the method developed by Magliocchetti et al. (1998), we vary the link-length in the percolation procedure according to the flux of each source. In that way, bright sources are combined, even if their angular separation is large, whereas faint sources are left as single objects. This technique is based on the $\theta-S$ relation for radio sources, which has been shown to follow $\theta \propto \sqrt S$ (Oort 1987a).

To define the relation between flux density and link-length, the angular separation of double sources versus their total flux is plotted in Fig. 1, out to a separation of 180arcsec. Visual inspection has confirmed that the pairs on the left of Fig. 1 are predominantly sub-components of a single source. This is based on an assessment of the appearance of the object, including the disposition of the sources, the nature of any bridging radiation, and the appearance of source edges. Accordingly, we set the maximum link-length to be

$$\theta_{\rm link} = 20 \times \sqrt{F_{\rm total}},$$ (7)

where $F_{\rm total}$ is the total flux of each group. This is shown by the dashed line in Fig. 1 and effectively removes the majority of visually identified doubles. Moreover, one can apply an additional criterion to identify genuine doubles, based on the relative flux densities of the sub-components (Magliocchetti et al. 1998). This is because lobes of a single radio source are expected to have correlated flux densities. Here, the groups of sources identified by the percolation technique are combined only if their fluxes differ by a factor of less than 4. This procedure was repeated until no new groups were found. The final catalogue consists of 908 objects to the limit of 0.1mJy, with a total of 30 groups of sources being identified and replaced.

The source counts of the sample, normalised to the Euclidean slope, are plotted in Fig. 2 along with the radio counts at 1.4GHz taken from Windhorst et al. (1993). There is a drop in the number counts below 0.5mJy, as our sample is affected by incompleteness. To quantify this, we firstly fit a straight line to the source counts of Windhorst et al. (1993) for flux densities fainter that 5mJy (continuous line in Fig. 2). We then compare our number counts at a given flux density bin with those predicted by the fitted line. We conclude that our sample is $\approx80\%$ complete to 0.4mJy. This is in agreement with the correction factors for incompleteness independently derived by Hopkins et al. (1998) accounting for both resolution effects and the attenuation of the beam away from the field centre. Therefore, to minimise the effect of incompleteness of the radio catalogue, when performing the correlation analysis, we restrict ourselves to a subsample containing all sources brighter than 0.4mJy.

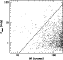Figure 1: Angular separation against total flux density of double sources. The dashed line represents the maximum link-length, for a given flux density, used in the percolation technique

Figure 2: Circles: source counts at 1.4GHz for the Phoenix Survey; Stars: source counts from Windhorst et al. (1993); Line: best fit to the Windhorst et al. (1993) source counts for flux densities less than 5mJy

Finally, before fitting a power law to $w(\theta )$, we take into account a bias arising from the finite boundary of the sample. Since the angular correlation function is calculated within a region of solid angle $\Omega$, the background projected density of sources, at a given flux density limit $S_{\rm o}$, is effectively $N_{\rm s}(S>S_{\rm o})/\Omega$ (where $N_{\rm s}(S>S_{\rm o})$ is the number of detected objects brighter than $S_{\rm o}$). However, this is an overestimation of the true underlying mean surface density, because of the positive correlation between galaxies in small separations, balanced by negative values of $w(\theta )$ at larger separations. This bias, known as the integral constraint, has the effect of reducing the amplitude of the correlation function by

$$\omega_{\Omega}=\frac{1}{\Omega ^{2}} \int{\int{w(\theta) {\rm d}\Omega_{1} {\rm d}\Omega_{2}}},$$ (8)

where $\Omega$ is the solid angle of the survey area. The angular constraint is estimated using Monte Carlo integration, assuming the correlation function to follow a power law $w(\theta)=A_{\omega} \times \theta ^{-\delta}$ with $\delta =0.8$ or 1.1. We find $\omega_{\Omega}=1.46A_{\omega}$ and $\omega_{\Omega}=1.89A_{\omega}$for $\delta =0.8$ and $\delta =1.1$ respectively, where $\theta$ is measured in degrees.