5 Corrections to redshifts and velocity dispersions

Figure 4: Histograms for the galaxies in the three sample regions and in the Coma cluster. Left: A histogram of the aperture sizes of the sample galaxies relative to the normalising aperture radius, with $r_{\rm ap}$ in units of kpc at the distance (redshift) of the galaxy, and 2 $r_{\rm norm}$ = 1.19 h-1 kpc, equivalent to 3.4 arcsec for a galaxy at the distance of the Coma cluster (h = 1 was used). Right: A histogram of the sizes of the aperture corrections applied to the sample galaxies; $\sigma _{\rm obs}$ is the raw observed value and $\sigma _{\rm cor}$ is the aperture-corrected value of the velocity dispersion

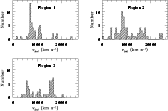
Figure 5: Histograms of heliocentric radial velocity for observed galaxies in the three sample regions. Bin width 500 km s-1

Figure 6: Comparison of results for heliocentric radial velocity values determined from repeat observations

Figure 7: Comparison of results for velocity dispersions measured from repeat observations

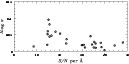Figure 8: The difference between results for velocity dispersions measured from repeat observations, plotted against the mean S/N per $\mbox{\AA}$ of each pair of spectra

5.1 Heliocentric correction to redshifts

Redshifts were corrected for the radial velocity of the template star and also corrected to the heliocentric system to take into account the motion of the Earth relative to the observed galaxy and the template star. This correction is included in fxcor; the result in the heliocentric frame is denoted $v_{\rm hel}$.

5.2 Aperture correction to velocity dispersions

In E and S0 galaxies there are radial gradients in the velocity dispersion, with a higher velocity dispersion in the center of the galaxy than in the outer regions (Davies & Birkinshaw 1988; Franx et al. 1989; Davies et al. 1993). For this reason the derived "central" velocity dispersion parameter depends on the distance of the galaxy and on the size of the aperture used for the observation of the spectrum. It is therefore necessary to apply an aperture correction to transform the observed parameters so that they are independent of distance and of the telescope used.

The measured value of velocity dispersion depends on the velocity dispersion profile in the galaxy. Since the profile is not known for each galaxy, a general form must be assumed. J$\o$rgensen et al. (1995) established an aperture correction from kinematic models based on the available literature data. They used the models to derive the equivalent circular aperture for each rectangular aperture, and adopted a power law as the aperture correction to $\sigma$. The radius $r_{\rm ap}$ (in arcsec) of the equivalent circular aperture is found from $r_{\rm ap} = 1.025 \sqrt(wl/\pi)$, where w and l are the width and length of a rectangular aperture (slit). J$\o$rgensen et al. (1995) correct the velocity dispersion to an aperture with a standard physical size, and use a value for the normalising aperture size of 2 $r_{\rm norm}$ = 1.19 h^-1kpc ( $h \equiv H_0$/100 km s^-1 Mpc^-1.) This means that the velocity dispersion values are normalized to a velocity dispersion measured with an aperture of diameter 1.19 h^-1 kpc, which is equivalent to 3.4 arcsec for a galaxy at the distance of the Coma cluster. Baggley (1996) has shown that it is necessary to also take the effective radius $r_{\rm e}$ into account in the aperture correction, since the observed velocity dispersion of a galaxy depends on $r_{\rm e}$as well. For two galaxies of different sizes at the same distance observed through the same aperture, the slit will cover more of the smaller galaxy and a different part of the galaxy profile will therefore be sampled; this dependence of $\sigma$ on $r_{\rm e}$ must be removed to ensure that the velocity dispersion is truly a distance-independent quantity. We used Baggley's formula for the aperture correction; it is a generalisation of the formula of J$\o$rgensen et al. (1995) to take $r_{\rm e}$ into account:

$$\,\log \frac{\sigma_{\rm cor}}{\sigma_{\rm obs}} = 0.038 \, ... ...}} \, \frac{r_{\rm e}^{\rm norm}}{r_{\rm e}^{\rm gal}}\right),$$ (1)

where: $\sigma _{\rm obs}$ is the value of the velocity dispersion found from observation through an aperture equivalent to $r_{\rm ap}$; $\sigma _{\rm cor}$ is the velocity dispersion value corrected to the adopted normalising aperture size $r_{\rm norm}$; $cz_{\rm gal}$ is the redshift of the galaxy; $cz_{\rm Coma}$ is the redshift of the Coma cluster; $r_{\rm e}^{\rm gal}$ is the effective radius of the galaxy; and $r_{\rm e}^{\rm norm}$ is the normalising effective radius, which is taken to be 20 arcsec, following Baggley (1996) - this is the mean $r_{\rm e}$ of the galaxies in the sample of J$\o$rgensen et al. (1995), which was used to derive the correction. This means that there will be no aperture correction for a galaxy with $r_{\rm e}$ = 20 arcsec, at the distance of the Coma cluster, observed through an aperture with an equivalent radius of 1.7 arcsec.

Equation (1) was used to calculate the corrections. The slit widths in the various instrumental setups are as shown in Table 2. For the length of the slit in the aperture, what is important is the extent of the galaxy along the slit, i.e. the length from which the one-dimensional spectrum was extracted; the spectrum was extracted out to the point where the luminosity had fallen to 10% of its peak value. The $r_{\rm e}$ value for each galaxy was taken from the results of the fitting and seeing-correction programs applied to the photometric data, as described in Müller (1997) and Müller et al. (1999). The value of the heliocentric redshift $cz_{\rm Coma}$ was taken to be 6917 km s^-1 (Zabludoff et al. 1993), and h = 1 was used in the conversion of km s^-1 to kpc.

The contribution to the aperture correction from the effect of $r_{\rm e}$ is more important than those for different slit sizes and different galaxy distances. From Eq. (1) it can be seen that the correction is negative for large or nearby objects (this is the case for the standard galaxies) and positive for galaxies with $r_{\rm e}$ less than 20 arcsec, which are smaller than or more distant than a 20 arcsec galaxy at the distance of Coma. The histogram of the applied aperture corrections in Fig. 4 shows that for the sample galaxies the correction is positive in most cases.