![\begin{displaymath}L(x)=P(y/x)\approx \prod_i\exp\left[-\frac{(y_i-(Hx)_i)^2}{2\sigma_i^2}\right]\cdot
\end{displaymath}](/articles/aas/full/1999/20/ds8516/img12.gif) |
(4) |
![\begin{displaymath}L(x)=P(y/x)\approx \prod_i\exp\left[-\frac{(y_i-(Hx)_i)^2}{2\sigma_i^2}\right]\cdot
\end{displaymath}](/articles/aas/full/1999/20/ds8516/img12.gif) |
(4) |
![\begin{displaymath}{\rm Log}[P(y/x)]\approx -\frac 12\sum_i\frac{(y_i-(Hx)_i)^2}{\sigma_i^2}
\end{displaymath}](/articles/aas/full/1999/20/ds8516/img13.gif) |
(5) |
| J(x) | = | ||
| = |  |
(6) |
Any iterative descent method may be used to minimize J(x).
Making use of the gradient expression:
| (7) |
| (8) |
The solution x* given by this algorithm when
![]() is the minimum
norm least squares solution (MNLS), which may be formally expressed as
x*=(HTRH)-1HTRy corresponding to the first order optimality condition:
is the minimum
norm least squares solution (MNLS), which may be formally expressed as
x*=(HTRH)-1HTRy corresponding to the first order optimality condition:
![]() .
.
However, the deconvolution problem is an ill-posed problem, and the MNLS algorithm produces numerical instabilities. The noise affecting the data is amplified during the restoration process.
Moreover the solution may have negative parts without physical meaning; this later point is overcome by using the constraint for a non-negative solution. Several algorithmic methods have been proposed for that, and in particular ISRA.
ISRA was initially proposed in a multiplicative form by Daube-Witherspoon &
Muehllehner (1986). The convergence of the algorithm was then analyzed by De Pierro
(1987, 1990, 1993), and Titterington (1987), and they show that the sequence obtained by
ISRA converges toward the solution of the problem:

In its original form, ISRA is written as:
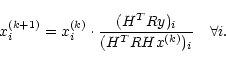 |
(9) |
The iterative algorithm given by Eq. (9) can straightforwardly be rewritten in the
additive form:
![\begin{displaymath}x_i^{(k+1)}=x_i^{(k)}+\frac{x_i^{(k)}}{(H^TRHx^{(k)})_i}[H^TR(y-Hx^{(k)})]_i.
\end{displaymath}](/articles/aas/full/1999/20/ds8516/img26.gif) |
(10) |
![\begin{displaymath}x^{(k+1)}=x^{(k)}+{\rm
diag}\left[\frac{x_i^{(k)}}{(H^TRHx^{(k)})_i}\right]H^TR(y-Hx^{(k)}),
\end{displaymath}](/articles/aas/full/1999/20/ds8516/img27.gif) |
(11) |
![\begin{displaymath}d^{(k)}={\rm diag}\left[\frac{x_i^{(k)}}{(H^TRHx^{(k)})_i}\right]H^TR(y-Hx^{(k)}).
\end{displaymath}](/articles/aas/full/1999/20/ds8516/img28.gif) |
(12) |
Evidently, for relaxed algorithms, the non-negativity of the solution as well as the convergence of the algorithm is not guaranteed; a specific analysis that goes beyond the scope of this paper would then become necessary.
![\begin{displaymath}L(x)=P(y/x)=\prod_i\frac{[(Hx)_i]^{y_i}}{y_i!}\exp[-(Hx)_i]\cdot
\end{displaymath}](/articles/aas/full/1999/20/ds8516/img31.gif) |
(13) |
![\begin{displaymath}T(x)\!=\!-{\rm Log}\left[L(x)\right]\!\approx\!\!\sum_i\left[(Hx)_i-y_i\right]+y_i{\rm
Log}\frac{y_i}{(Hx)_i}\cdot
\end{displaymath}](/articles/aas/full/1999/20/ds8516/img32.gif) |
(14) |
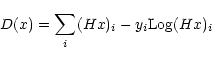 |
(15) |
![\begin{displaymath}x_i^{(k+1)}=\frac{1}{a_i}x_i^{(k)}\left[H^T\frac{y}{Hx^{(k)}}\right]_i
\end{displaymath}](/articles/aas/full/1999/20/ds8516/img34.gif) |
(16) |
This algorithm was previously proposed by Richardson (1972) and by Lucy (1974) in
the field of Astrophysics. Shepp & Vardi (1982) and Byrne (1993) show that the convergence
hold, and that the sequence generated by this algorithm also satisfies the Kuhn-Tucker
optimality conditions for the constrained minimization problem: Min/x: D(x), ![]() .
As for ISRA, all successive estimates remain positive if the initial estimate is positive.
Moreover, if a component of the solution is set to zero, or becomes equal to zero, it remains
equal to zero for all successive iterations.
.
As for ISRA, all successive estimates remain positive if the initial estimate is positive.
Moreover, if a component of the solution is set to zero, or becomes equal to zero, it remains
equal to zero for all successive iterations.
Here again, it is interesting to write RLA in the additive form:
![\begin{displaymath}x_i^{(k+1)}=x_i^{(k)}+\frac{x_i^{(k)}}{a_i}\!\!\left[H^T{\rm ...
...\!\left[\frac{1}{(Hx^{(k)})}_i\right]\!\!(y-Hx^{(k)})\right]_i
\end{displaymath}](/articles/aas/full/1999/20/ds8516/img38.gif) |
(17) |
![\begin{displaymath}x^{(k{+}1)}{=}x^{(k)}{+}{\rm diag}\!\!\left[\frac{x_i^{(k)}}{...
...iag}\!\!\left[\frac{1}{(Hx^{(k)})_i}\right]\!\!(y{-}Hx^{(k)}).
\end{displaymath}](/articles/aas/full/1999/20/ds8516/img39.gif) |
(18) |

\end{displaymath}](/articles/aas/full/1999/20/ds8516/img40.gif) |
(19) |
![\begin{displaymath}x^{(k+1)}=x^{(k)}+{\rm diag}\left[\frac{x_i^{(k)}}{a_i}\right]
\left[-\nabla D(x^{(k)})\right].
\end{displaymath}](/articles/aas/full/1999/20/ds8516/img43.gif) |
(20) |
i) The additive forms of ISRA and RLA evidence the similar roles played by the
weighting matrix
![]() in Eq. (11) and by the matrix
in Eq. (11) and by the matrix
![]() in Eq. (18). These quantities both correspond to variances of the
signal. For the Gaussian process,
in Eq. (18). These quantities both correspond to variances of the
signal. For the Gaussian process,
![]() is the variance of the intensity in a pixel. For
the Poisson process
(Hx(k))i also represents the variance of the signal, because for this
process the variance equals the mean.
is the variance of the intensity in a pixel. For
the Poisson process
(Hx(k))i also represents the variance of the signal, because for this
process the variance equals the mean.
ii) In the Gaussian case, J (x) is a quadratic form, the convexity of this objective
function allows to obtain the solution by solving the linear system
![]() .
The
Gradient or Conjugate Gradient methods in their classical form leading to linear algorithms
may be used in this case and the stepsize is known explicitly. We must observe that the
non-linearity of the algorithm ISRA is introduced only by the non-negativity constraint.
.
The
Gradient or Conjugate Gradient methods in their classical form leading to linear algorithms
may be used in this case and the stepsize is known explicitly. We must observe that the
non-linearity of the algorithm ISRA is introduced only by the non-negativity constraint.
On the contrary, in the Poisson case, the functional D(x), although convex, is not quadratic. Thus, the non-linearity of the RLA algorithm is due to the particular form of D (x) as well as to the non-negativity constraint.
iii) For the two algorithms, we set the initial estimate to a constant value:
![]() where N is the number of pixels in the image; moreover the integral of the image is
generally normalized to 1. We must observe that in the RLA algorithm we have for all k:
where N is the number of pixels in the image; moreover the integral of the image is
generally normalized to 1. We must observe that in the RLA algorithm we have for all k:
![]() ,
which is not the case for ISRA; this is due to the fact that the
functional D(x) implicitly contains the constant intensity constraint:
,
which is not the case for ISRA; this is due to the fact that the
functional D(x) implicitly contains the constant intensity constraint:
![]() together with
together with
![]() ,
these later property
appearing naturally for the PSF in a deconvolution problem or being imposed in the
algorithm.
,
these later property
appearing naturally for the PSF in a deconvolution problem or being imposed in the
algorithm.
In the case of ISRA, the conservation of the total intensity of the image is ensured by normalization after each iteration.
iv) The two algorithms are not regularized. A non-negativity constraint, although necessary, does not produce smooth solutions. When the iteration number increases too much, the classical phenomena of instability appear in the solutions. On the practical point of view, the iteration number must be limited to obtain an acceptable compromise between resolution and stability of the solutions; this allows some regularization. Alternatively, an explicit regularization may be done by introducing a supplementary constraint to attenuate the high frequency components in the solution; this will be proposed in a future paper.
We have performed a numerical simulation to illustrate some features of the deconvolution procedures described in the previous sections; the computations are made using Mathematica (Wolfram 1996).
![\begin{figure}
\includegraphics[width=9.5cm]{figure2.eps}\end{figure}](/articles/aas/full/1999/20/ds8516/Timg53.gif) |
Figure 2: Simulated noisy images: Poisson statistics. Representations of the blurred image of Fig. 1 observed with 104 photoelectrons (left) and 106 photoelectrons (right) |
![\begin{figure}
\includegraphics[width=9.5cm]{figure3.eps}\end{figure}](/articles/aas/full/1999/20/ds8516/Timg54.gif) |
Figure 3: Simulated noisy images: representations of the blurred image of Fig. 1 observed with a level of additive Gaussian noise of strength comparable to that of Fig. 2 |
The object x is chosen to represent an ensemble of three stars, with different diameters and centers to limb variations. A bright and dark sunspot-like feature is added to the larger star's atmosphere. The PSF h is a realistic representation of the PSF of a true telescope. It is computed as the squared modulus of the Fourier Transform of a function representing the telescope aperture with a small phase aberration. It may correspond to observing conditions with the Hubble Space Telescope operating in the far ultraviolet (Gilliland & Dupree 1996). The resulting Optical Transfer Function is then a low pass filter, limited in spatial frequencies to the extent of the aperture autocorrelation function. The observed filtered image y is then strictly band limited. This particular property is of interest for the study of the reconstructed image in the Fourier plane discussed below.
Figures 2 and 3 represent possible detected image in the case of Poisson and Gaussian statistics. Figure 2 represents the observed image assuming a perfect photodetection, for two levels of noise corresponding to a total of 104 and 106 photoelectrons in the image. Such images may be obtained in visible observations. Figure 3 represents the observed image corrupted by additive Gaussian noise and may correspond to infrared observations with noise coming from the detector and the background.
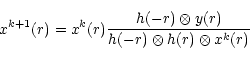 |
(21) |
and for RLA:
![\begin{displaymath}x^{k+1} ( r )=x^k ( r )\left[h(-r)\otimes \left\{\frac{y ( r ) }{h ( r ) \otimes x^k ( r
)}\right\}\right]
\end{displaymath}](/articles/aas/full/1999/20/ds8516/img61.gif) |
(22) |
The results of the deconvolutions for the two different statistics are presented in the following three figures. Figures 4 and 5 give the results obtained for the deconvolution of Fig. 2, while Fig. 6 gives an example of the results obtained for an additive signal-independent Gaussian noise. The results are presented for different iterations number "k''. As k increases, the image becomes sharper, but the noise increases too. When doing with real data, it is extremely difficult to determine what is the best-reconstructed image, i.e. when to stop the iteration. In a numerical simulation, we can obviously answer this question. Aside a visual comparison between the results and the object, we have used as criterion of quality the simple Euclidean Distance (ED)- between the true object and the reconstructed image. On this basis, for Poisson noise, we found the results of RLA slightly better than those of ISRA. This is not surprising, since RLA is constructed for the Poisson statistic. However, the differences between ISRA and RLA results are almost insignificant, as it can be deduced by a simple visual inspection of the results. To the contrary, ISRA gives much better results than RLA for Gaussian statistics. This is also expected, but in this case, the difference is strongest. This can be clearly seen in Fig. 6. Moreover, ISRA is almost insensitive to small negative value present in the signal (these negative values appear when the average value of the background is subtracted). For RLA, an offset must be used to reconstruct the image to deal with positive values only. This difference in behavior can be easily understood considering that ISRA works on the ratio of two smooth expressions (HTy over HTHx) while RLA does the smoothing by HT after taking the ratio y over Hx.
Figure 7 clearly shows that the reconstructed images present energy outside the frequency limit of the telescope. These effects are in part due to the non-linearity of these algorithms. The three top curves of this figure correspond to the modulus of the Fourier Transforms of the images of Fig. 1. In this representation, the zero frequency is at the center of the image. As already indicated, the resulting blurred image has no frequency power outside the dish zone corresponding to the aperture autocorrelation function.
The three bottom curves of Fig. 7 represent the modulus of the Fourier Transforms of the reconstructed images. The example is given for RLA at iterations numbers 1, 5 and 20, for the 104 photoelectrons image, but similar results can be obtained for ISRA. The iterative algorithms rapidly produce power outside the limits of the original blurred image, i.e. in a region of the Fourier plane fully dominated by the noise. The extent of frequencies is inherent to the iterative algorithms used. Figure 8 gives a measure of this excess of signal outside the cut-off frequency by giving, as a function of the iteration number, the ratio of the integral of Abs[Xk(u)] outside the cut-off frequency to the integral of Abs[Xk(u)] inside the cut-off frequency. This behavior is still observed when a noiseless image is processed.
Copyright The European Southern Observatory (ESO)