

Up: Comparison between ISRA and
In the deconvolution problem, for a Gaussian additive noise and in the case of real functions
we must compute the gradient of the function
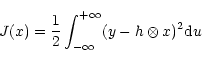 |
(A1) |
y, h, x depends on u.
Considering for the variable x, an increase "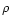 '' in the general direction "s'',
we have:
'' in the general direction "s'',
we have:
![\begin{displaymath}=\frac 12\int^{+\infty}_{-\infty}\left[y^2-2y(h\otimes (x+\rho s))+(h\otimes
(x+\rho s))^2\right].
\end{displaymath}](/articles/aas/full/1999/20/ds8516/img85.gif) |
(A2) |
Expanding this function and neglecting the second order terms, we have:
![\begin{displaymath}J(x+\rho s)=J(x)+\rho\int^{+\infty}_{-\infty}(h\otimes s)[(h\otimes x)-y]{\rm d}u
\end{displaymath}](/articles/aas/full/1999/20/ds8516/img86.gif) |
(A3) |
this expression must be identical to:
 .
.
With:
$](/articles/aas/full/1999/20/ds8516/img88.gif) ,
expanding the convolution product between
h and s, we have:
,
expanding the convolution product between
h and s, we have:
![\begin{displaymath}J'(x,s)=\left[\int^{u=+\infty}_{u=-\infty}H(u)\int^{t=+\infty}_{t=-\infty} s(t)h(u-t){\rm
d}t {\rm d}u\right]
\end{displaymath}](/articles/aas/full/1999/20/ds8516/img89.gif) |
(A4) |
or, inverting the integrals
![\begin{displaymath}J'(x,s)=\left[\int^{t=+\infty}_{t=-\infty}s(t)\int^{u=+\infty}_{u=-\infty}
H(u)h(u-t){\rm d}u {\rm d}t\right]
\end{displaymath}](/articles/aas/full/1999/20/ds8516/img90.gif) |
(A5) |
letting: z=u-t, we have:
![\begin{displaymath}J'(x,s)=\left[\int^{t=+\infty}_{t=-\infty}s(t) \int^{z=+\infty}_{z=-\infty}H(z+t)h(z){\rm d}z
{\rm d}t\right]
\end{displaymath}](/articles/aas/full/1999/20/ds8516/img91.gif) |
(A6) |
which can be written in the form:
![\begin{displaymath}J'(x,s)=\left[\int^{t=+\infty}_{t=-\infty}s(t)\{h(-t)\otimes H(t)\}{\rm d}t\right].
\end{displaymath}](/articles/aas/full/1999/20/ds8516/img92.gif) |
(A7) |
Using the expression of the derivative of J(x) at x in the direction s we obtain:
![\begin{displaymath}\nabla J(x)=h(-u)\otimes \{[h(u)\otimes x(u)]-y(u)\}\cdot
\end{displaymath}](/articles/aas/full/1999/20/ds8516/img93.gif) |
(A8) |


Up: Comparison between ISRA and
Copyright The European Southern Observatory (ESO)
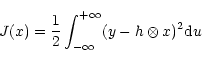
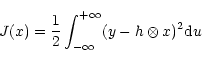
![]() '' in the general direction "s'',
we have:
'' in the general direction "s'',
we have:
![\begin{displaymath}=\frac 12\int^{+\infty}_{-\infty}\left[y^2-2y(h\otimes (x+\rho s))+(h\otimes
(x+\rho s))^2\right].
\end{displaymath}](/articles/aas/full/1999/20/ds8516/img85.gif)
![\begin{displaymath}J(x+\rho s)=J(x)+\rho\int^{+\infty}_{-\infty}(h\otimes s)[(h\otimes x)-y]{\rm d}u
\end{displaymath}](/articles/aas/full/1999/20/ds8516/img86.gif)
![]() ,
expanding the convolution product between
h and s, we have:
,
expanding the convolution product between
h and s, we have:
![\begin{displaymath}J'(x,s)=\left[\int^{u=+\infty}_{u=-\infty}H(u)\int^{t=+\infty}_{t=-\infty} s(t)h(u-t){\rm
d}t {\rm d}u\right]
\end{displaymath}](/articles/aas/full/1999/20/ds8516/img89.gif)
![\begin{displaymath}J'(x,s)=\left[\int^{t=+\infty}_{t=-\infty}s(t)\int^{u=+\infty}_{u=-\infty}
H(u)h(u-t){\rm d}u {\rm d}t\right]
\end{displaymath}](/articles/aas/full/1999/20/ds8516/img90.gif)
![\begin{displaymath}J'(x,s)=\left[\int^{t=+\infty}_{t=-\infty}s(t) \int^{z=+\infty}_{z=-\infty}H(z+t)h(z){\rm d}z
{\rm d}t\right]
\end{displaymath}](/articles/aas/full/1999/20/ds8516/img91.gif)
![\begin{displaymath}J'(x,s)=\left[\int^{t=+\infty}_{t=-\infty}s(t)\{h(-t)\otimes H(t)\}{\rm d}t\right].
\end{displaymath}](/articles/aas/full/1999/20/ds8516/img92.gif)