

Up: Comparison between ISRA and
A computation analogous to the previous one can be performed in the case of a
Poisson process. In this case, we must compute the gradient of:
![\begin{displaymath}J(x)=\int^{x=+\infty}_{x=-\infty}[(h\otimes x)-y{\rm Log}(h\otimes x)]{\rm d}u.
\end{displaymath}](/articles/aas/full/1999/20/ds8516/img94.gif) |
(B1) |
Considering for the variable "x'', an increase "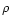 '' in the
general direction "s'', we have:
'' in the
general direction "s'', we have:
![\begin{displaymath}+\rho(h\otimes s)\}-y
{\rm Log}\left\{(h\otimes x)(1+\rho\frac{(h\otimes s)}{(h\otimes x)}\right\}
\Biggr]{\rm d}u
\end{displaymath}](/articles/aas/full/1999/20/ds8516/img99.gif) |
(B3) |
![\begin{displaymath}-y{\rm Log}\left\{1+\rho\frac{(h\otimes s)}{(h\otimes
x)}\right\}\Biggr]{\rm d}u
\end{displaymath}](/articles/aas/full/1999/20/ds8516/img101.gif) |
(B4) |
with a first order series expansion:
![\begin{displaymath}-y
{\rm Log}(h\otimes x)-y\rho\frac{(h\otimes s)}{(h\otimes x)}\Biggr]{\rm d}u
\end{displaymath}](/articles/aas/full/1999/20/ds8516/img103.gif) |
(B5) |
then
![\begin{displaymath}+\rho\int^{u=+\infty}_{u=-\infty}\left[(h\otimes s)-y\frac{(h\otimes
s)}{(h\otimes x)}\right]{\rm d}u
\end{displaymath}](/articles/aas/full/1999/20/ds8516/img105.gif) |
(B6) |
comparing this relation with:
 we have :
we have :
![\begin{displaymath}J'(x,s)=\int^{u=+\infty}_{u=-\infty}\left[(h\otimes s) -y\frac{(h\otimes s)}{(h\otimes
x)}\right]{\rm d}u
\end{displaymath}](/articles/aas/full/1999/20/ds8516/img106.gif) |
(B7) |
that is:
{\rm
d}u
\end{displaymath}](/articles/aas/full/1999/20/ds8516/img107.gif) |
(B8) |
with the integral form of the convolution product, we have:
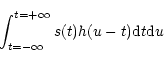 |
(B9) |
or, re-ordering the integrals:
![\begin{displaymath}\int^{u=+\infty}_{u=-\infty}\left[1-\frac{y}{(h\otimes x)}
\right]h(u-t){\rm d}u{\rm d}t.
\end{displaymath}](/articles/aas/full/1999/20/ds8516/img111.gif) |
(B10) |
Let:
![\begin{displaymath}H(u)=\left[1-\frac{y(u)}{(h(u)\otimes x(u))}\right]
\end{displaymath}](/articles/aas/full/1999/20/ds8516/img112.gif) |
(B11) |
with the change of variables: z=u-t, we obtain:
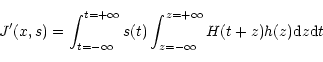 |
(B12) |
that is:
![\begin{displaymath}J'(x,s)=\int^{t=+\infty}_{t=-\infty}s(t)[h(-t)\otimes H(t)]{\rm d}t.
\end{displaymath}](/articles/aas/full/1999/20/ds8516/img114.gif) |
(B13) |
Using the definition of the derivative of J(x) at x in the direction s we obtain:
![\begin{displaymath}\nabla J(x)=h(-u)\otimes \left[1-\frac{y(u)}{h(u)\otimes x(u)}\right]\cdot
\end{displaymath}](/articles/aas/full/1999/20/ds8516/img115.gif) |
(B14) |
Acknowledgements
We are grateful to Professor Jean CEA for stimulating discussions, in
particular for help in the formulation of the appendices.


Up: Comparison between ISRA and
Copyright The European Southern Observatory (ESO)
![\begin{displaymath}J(x)=\int^{x=+\infty}_{x=-\infty}[(h\otimes x)-y{\rm Log}(h\otimes x)]{\rm d}u.
\end{displaymath}](/articles/aas/full/1999/20/ds8516/img94.gif)
![\begin{displaymath}J(x)=\int^{x=+\infty}_{x=-\infty}[(h\otimes x)-y{\rm Log}(h\otimes x)]{\rm d}u.
\end{displaymath}](/articles/aas/full/1999/20/ds8516/img94.gif)
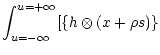
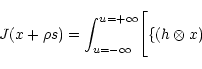
![\begin{displaymath}+\rho(h\otimes s)\}-y
{\rm Log}\left\{(h\otimes x)(1+\rho\frac{(h\otimes s)}{(h\otimes x)}\right\}
\Biggr]{\rm d}u
\end{displaymath}](/articles/aas/full/1999/20/ds8516/img99.gif)

![\begin{displaymath}-y{\rm Log}\left\{1+\rho\frac{(h\otimes s)}{(h\otimes
x)}\right\}\Biggr]{\rm d}u
\end{displaymath}](/articles/aas/full/1999/20/ds8516/img101.gif)
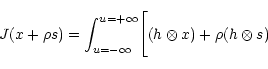
![\begin{displaymath}-y
{\rm Log}(h\otimes x)-y\rho\frac{(h\otimes s)}{(h\otimes x)}\Biggr]{\rm d}u
\end{displaymath}](/articles/aas/full/1999/20/ds8516/img103.gif)
![\begin{displaymath}J(x+\rho s)=
\int^{u=+\infty}_{u=-\infty}\bigl[(h\otimes x)
-y
{\rm Log}(h\otimes
x)\bigr]{\rm d}u
\end{displaymath}](/articles/aas/full/1999/20/ds8516/img104.gif)
![\begin{displaymath}+\rho\int^{u=+\infty}_{u=-\infty}\left[(h\otimes s)-y\frac{(h\otimes
s)}{(h\otimes x)}\right]{\rm d}u
\end{displaymath}](/articles/aas/full/1999/20/ds8516/img105.gif)
![\begin{displaymath}J'(x,s)=\int^{u=+\infty}_{u=-\infty}\left[(h\otimes s) -y\frac{(h\otimes s)}{(h\otimes
x)}\right]{\rm d}u
\end{displaymath}](/articles/aas/full/1999/20/ds8516/img106.gif)
{\rm
d}u
\end{displaymath}](/articles/aas/full/1999/20/ds8516/img107.gif)
![\begin{displaymath}J'(x,s)=
\int^{u=+\infty}_{u=-\infty}\left[1-\frac{y}{(h\otimes
x)}\right]
\end{displaymath}](/articles/aas/full/1999/20/ds8516/img108.gif)
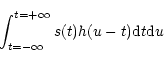
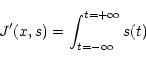
![\begin{displaymath}\int^{u=+\infty}_{u=-\infty}\left[1-\frac{y}{(h\otimes x)}
\right]h(u-t){\rm d}u{\rm d}t.
\end{displaymath}](/articles/aas/full/1999/20/ds8516/img111.gif)
![\begin{displaymath}H(u)=\left[1-\frac{y(u)}{(h(u)\otimes x(u))}\right]
\end{displaymath}](/articles/aas/full/1999/20/ds8516/img112.gif)
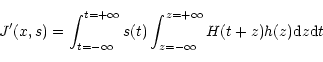
![\begin{displaymath}J'(x,s)=\int^{t=+\infty}_{t=-\infty}s(t)[h(-t)\otimes H(t)]{\rm d}t.
\end{displaymath}](/articles/aas/full/1999/20/ds8516/img114.gif)
![\begin{displaymath}\nabla J(x)=h(-u)\otimes \left[1-\frac{y(u)}{h(u)\otimes x(u)}\right]\cdot
\end{displaymath}](/articles/aas/full/1999/20/ds8516/img115.gif)