We describe here the implementation of a new objective-stopping technique that is based on the comparison of the results of these algorithms (RLA or ISRA) with that of the optimum Wiener filter. The principle of the approach was recently proposed in an ESO/NOAO Conference (Lanteri et al. 1998). Fundamentally, it consists of selecting the iteration number k for ISRA (or RLA) that gives a result close to that of the Wiener filter. This technique could also be used to determine the optimal regularization factor when an explicit regularization is performed.
The idea is to take advantage of the two kinds of algorithms. The final reconstructed image is given by ISRA (or RLA) and therefore has an ensemble of interesting properties, such as it is non-negative. Closeness with the optimum Wiener solution ensures that the reconstructed image is not too much corrupted by noise, as wished.
The Wiener filter has the advantage of being defined from physical considerations on SNR in the Fourier plane. It is based on the simple fact that spatial frequency components are differently corrupted by noises. For correctly sampled data, low and intermediate spatial frequencies are likely to contain more signal than noise, and the highest spatial frequencies components tend to contain essentially pure noise. It is clear for example, that the spectral energy detected outside the cut-off frequency of the telescope used is entirely due to noise, or to algorithmic artifacts. The Wiener technique is well known (Brault & White 1971) and we just present here the main features.
The Wiener filter operates in the Fourier plane. Let u denote the two-dimensional
spatial (or angular) frequency (u1 u2). Let Y(u), H(u) and
![]() denote
the Fourier transforms of the observed image, point spread function and of the reconstructed
Wiener image, respectively. In optics, the quantity H(u) is the optical transfer function.
denote
the Fourier transforms of the observed image, point spread function and of the reconstructed
Wiener image, respectively. In optics, the quantity H(u) is the optical transfer function.
We have:
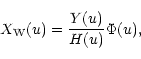 |
(23) |
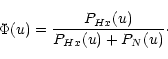 |
(24) |
In our original proposal (Lanteri et al. 1998), we suggested to compare the overall
effect of the Wiener procedure Abs
![]() on the modulus of the spatial
frequencies to the equivalent quantity Abs
[X(k)(u)/Y(u)] obtained for ISRA or RLA
during the iteration, and to choose the value of k for which these modulation transfer function
best agree. In practice, depending on possible near-zero values of H(u) and Y(u), these
quantities tend to present unwanted peaks that make difficult the computation of a distance
between them.
on the modulus of the spatial
frequencies to the equivalent quantity Abs
[X(k)(u)/Y(u)] obtained for ISRA or RLA
during the iteration, and to choose the value of k for which these modulation transfer function
best agree. In practice, depending on possible near-zero values of H(u) and Y(u), these
quantities tend to present unwanted peaks that make difficult the computation of a distance
between them.
In the present work, we propose as a measure of goodness-of-fit between the images
given by the iterative algorithms and the Wiener filter, the Euclidean distances
![]() between modules of spatial frequencies of the images:
between modules of spatial frequencies of the images:
| (25) |
A numerical simulation is made using the data material presented in Sect. 2; for the sake of conciseness, we limit the presentation to the case of Poisson noise. The Wiener filter is constructed taking for PHx(u) the squared modulus of the Fourier transform of the noiseless blurred image. The noise power spectrum PN(u) is determined as the average noise value outside the frequency cut-off of the telescope.
Wiener images corresponding to the deconvolution of Fig. 2 are shown in Fig. 9. For the two reconstructed images in the Wiener procedure, about 45% of the reconstructed pixels are negative. The total negative part corresponds to about 7% of the positive parts for the 104 photons image, and 4% for the 106 photons image.
The modulus of the Fourier transform of these images is used to compute the distance
![]() defined by Eq. (25). It is represented in Figs. 10 for ISRA and RLA, and
compared to the Euclidean distance
defined by Eq. (25). It is represented in Figs. 10 for ISRA and RLA, and
compared to the Euclidean distance
![]() between xk and the object. For the
104 photons image, the minimum values of
between xk and the object. For the
104 photons image, the minimum values of
![]() and
and
![]() perfectly
coincides for both algorithms (iteration # 7 ISRA, iteration # 6 for RLA). For the 106
photons image, the minimum values of
perfectly
coincides for both algorithms (iteration # 7 ISRA, iteration # 6 for RLA). For the 106
photons image, the minimum values of
![]() is obtained earlier than expected (iteration
# 92 instead of # 164 for ISRA, iteration # 81 instead of # 134 for RLA). In this later case
the use of the minimum value of
is obtained earlier than expected (iteration
# 92 instead of # 164 for ISRA, iteration # 81 instead of # 134 for RLA). In this later case
the use of the minimum value of
![]() tends to stop the iteration prematurely, but still
give a valuable order for stopping the iterations.
tends to stop the iteration prematurely, but still
give a valuable order for stopping the iterations.
In Figs. 11A and 11B, we give a comparison of the overall effect produced on the
spatial frequencies of the images. For each spatial frequency "u'', the ratios
![]() for ISRA and RLA are compared with the equivalent
quantity given by the Wiener filter
for ISRA and RLA are compared with the equivalent
quantity given by the Wiener filter
![]() .
To obtain smoother results,
we have represented, for each modulus of frequency | u|, the ratio of the circular average of
Abs
[X(k)(u)] and Abs
.
To obtain smoother results,
we have represented, for each modulus of frequency | u|, the ratio of the circular average of
Abs
[X(k)(u)] and Abs
![]() to the equivalent circular average of Abs[Y(u)]. The
comparison is limited to the results obtained in the Poisson statistics.
to the equivalent circular average of Abs[Y(u)]. The
comparison is limited to the results obtained in the Poisson statistics.
For a given image, the equivalent filters obtained for ISRA and RLA are very similar. In the very low range of frequencies, all curves tend to fit the inverse filter. In the intermediate range of frequencies, there is a rather good agreement between the best results of the iterative algorithms and the Wiener filter. In the highest frequencies, the iterative algorithms are very soon much higher than the Wiener filter. A good agreement between ISRA or RLA and Wiener in all range of frequencies would require an explicit regularization.
Copyright The European Southern Observatory (ESO)