

Up: Accuracy of radial-velocity measurements
Subsections
In this section, we present the expected mismatch errors
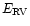 of the individual spectral regions.
We recall that
each is defined as the maximum mismatch shift (in absolute
value) out of the 14 different mismatch cases
(two steps of
of the individual spectral regions.
We recall that
each is defined as the maximum mismatch shift (in absolute
value) out of the 14 different mismatch cases
(two steps of  250 K in
250 K in
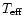 and one step of
and one step of  0.2 dex
in logg; see Sect. 3.2). We discuss these results for the 30
main-grid spectra considered,
i.e. for the 5 values of temperature, 1 of surface gravity,
and 6 of rotational velocity, representing the rotating
A-type main-sequence stars (see Sect. 3.3).
First, in Sect. 4.1, we look in more detail at the individual mismatch shifts
arising from the 14 different mismatch cases.
0.2 dex
in logg; see Sect. 3.2). We discuss these results for the 30
main-grid spectra considered,
i.e. for the 5 values of temperature, 1 of surface gravity,
and 6 of rotational velocity, representing the rotating
A-type main-sequence stars (see Sect. 3.3).
First, in Sect. 4.1, we look in more detail at the individual mismatch shifts
arising from the 14 different mismatch cases.
The step in (
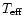 ,
logg) of the mismatch grid
as chosen in Sect. 3.2 needs to be sufficiently small
to sample properly the mismatch error
,
logg) of the mismatch grid
as chosen in Sect. 3.2 needs to be sufficiently small
to sample properly the mismatch error
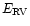 as a function
of
as a function
of
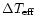 and
and
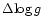 .
We are satisfied that the latter requirement
has in fact been met because a simple four-parameter model
(
.
We are satisfied that the latter requirement
has in fact been met because a simple four-parameter model
(
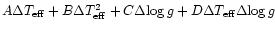 )
fits the 14 mismatch shifts fairly well for most spectral
regions in all main-grid spectra.
We also found that the maximum mismatch shift, i.e. the mismatch error
)
fits the 14 mismatch shifts fairly well for most spectral
regions in all main-grid spectra.
We also found that the maximum mismatch shift, i.e. the mismatch error
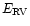 ,
for
,
for
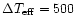 K (i.e. for 14 mismatch cases)
is twice that for
K (i.e. for 14 mismatch cases)
is twice that for
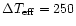 K (i.e. for 8 mismatch cases),
with an rms deviation less than 0.5 for all
30 main-grid spectra and for all spectral regions.
K (i.e. for 8 mismatch cases),
with an rms deviation less than 0.5 for all
30 main-grid spectra and for all spectral regions.
![\begin{figure}
\includegraphics[width=12cm]{fig_split.eps}\end{figure}](/articles/aas/full/1999/19/h1521/Timg35.gif) |
Figure 2:
Percentage of individual metal-line regions with a positive mismatch
shift for those mismatch cases with
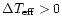 (full line),
and for those with
(full line),
and for those with
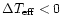 (dashed line).
All mismatch cases in logg are taken together.
Results are shown for each of the 30 spectra separately with
the numerical labels
referring to their
(dashed line).
All mismatch cases in logg are taken together.
Results are shown for each of the 30 spectra separately with
the numerical labels
referring to their
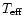 (1=7500K, 2=8000K,
3=8500K, 4=9000K, 5=9500K).
If
(1=7500K, 2=8000K,
3=8500K, 4=9000K, 5=9500K).
If
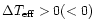 ,
the mismatch shift is that of
a hotter (cooler) object with respect to the template whose ,
the mismatch shift is that of
a hotter (cooler) object with respect to the template whose
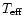 is referred to by their labels is referred to by their labels |
As pointed out in Sect. 1, if spectra have a high line-density one tends to
assume that, for a given mismatch case,
the mismatch shifts caused by
individual blends in a given spectrum
are like random numbers distributed symmetrically
around zero. Visual inspection of our mismatch shifts
(see e.g. Fig. 2)
suggests that, on the contrary they have a
preferential sign in different spectral regions for many
of the spectra and mismatch cases.
Although the wavelength regions defined in
Sect. 3.4 do not isolate individual blends, those without hydrogen
lines are sufficiently narrow and numerous to allow a limited verification
of the assumption of randomness of the sign.
For each of the 420 samples of mismatch shifts taken from all
metal-line regions (for 14 mismatch cases in 30 spectra),
we tested the hypothesis that the sign of the shifts in the sample is random.
The results can be summarized as follows:
-
at the 5% significance level the hypothesis cannot be rejected for any
of the 30 spectra if the mismatch is caused only by differences
in logg and not in
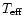 ;
;
-
likewise it cannot be rejected for any mismatch case if the template spectrum
has vsini = 5 or 50 kms-1;
-
however, for all temperatures there are one or two
vsini values and several mismatch cases for which the hypothesis
must indeed be rejected at the 5% level, with a slight preponderance
of cases with
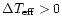 ,
,
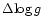 = 0 and
= 0 and
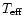 > 7500 K;
the total number of these cases is 110, and in 42
out of them the hypothesis must be rejected even at the 1% level
so it is quite unlikely that they could be ascribed to coincidence.
> 7500 K;
the total number of these cases is 110, and in 42
out of them the hypothesis must be rejected even at the 1% level
so it is quite unlikely that they could be ascribed to coincidence.
A characteristic of these trends is
illustrated in Fig. 2, where a strong
correlation appears between the sign of the temperature mismatch
and the sign of the corresponding mismatch shift, for most metal-line regions
and for rotational velocities above 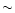 50 kms-1.
The correlation exists for all temperatures, although the scatter
increases towards the highest vsini because of the smaller number
of regions defined.
The reason for this common behaviour of most spectral regions has yet to
be investigated by examining the origin of each shift.
Positional relations between the lines of
multiplets contributing to temperature-dependent blends in different regions
presumably play a role.
The important consequence is that, at least for faster rotators,
a majority of the metal-line blends may cause a mismatch shift in the same
sense so that one cannot be certain of reducing systematic errors simply
by including more such blends in a cross-correlation.
This will strongly influence
the extent to which it is useful to combine
individual spectral regions as is discussed in Sect. 5.1.
50 kms-1.
The correlation exists for all temperatures, although the scatter
increases towards the highest vsini because of the smaller number
of regions defined.
The reason for this common behaviour of most spectral regions has yet to
be investigated by examining the origin of each shift.
Positional relations between the lines of
multiplets contributing to temperature-dependent blends in different regions
presumably play a role.
The important consequence is that, at least for faster rotators,
a majority of the metal-line blends may cause a mismatch shift in the same
sense so that one cannot be certain of reducing systematic errors simply
by including more such blends in a cross-correlation.
This will strongly influence
the extent to which it is useful to combine
individual spectral regions as is discussed in Sect. 5.1.
For each of the 30 main-grid spectra we plotted the distribution of mismatch
errors
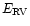 from the different spectral regions.
A Kolmogorov-Smirnov test shows that, for a given rotational velocity,
the hypothesis that the distributions for the 5 different temperatures
are identical cannot be rejected,
although the relatively small
number of regions must influence that result.
We can therefore combine the results for all
from the different spectral regions.
A Kolmogorov-Smirnov test shows that, for a given rotational velocity,
the hypothesis that the distributions for the 5 different temperatures
are identical cannot be rejected,
although the relatively small
number of regions must influence that result.
We can therefore combine the results for all
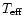 ;
Fig. 3 shows the distributions for the 6 values
of vsini. It is immediately apparent that a large range in
;
Fig. 3 shows the distributions for the 6 values
of vsini. It is immediately apparent that a large range in
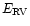 exists among the different regions at any given vsini:
the 10% highest errors are on average about a factor 20 larger
than the 10% smallest ones.
exists among the different regions at any given vsini:
the 10% highest errors are on average about a factor 20 larger
than the 10% smallest ones.
![\begin{figure}
\includegraphics[width=20cm]{fig_distr.eps}\end{figure}](/articles/aas/full/1999/19/h1521/Timg36.gif) |
Figure 3:
Distribution of the mismatch errors
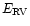 from all spectral
regions.
For each value of vsini, the results from the 5 values of
from all spectral
regions.
For each value of vsini, the results from the 5 values of
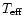 are combined. Results for H-line regions are shown hashed are combined. Results for H-line regions are shown hashed |
The most important characteristic of these distributions is the
strong and consistent increase in the errors with vsini.
In Sect. 4.3 we will quantify that dependence in more detail.
Although the distributions of all
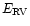 for different temperatures
are indistinguishable, the mismatch error of each individual
region may vary significantly with
for different temperatures
are indistinguishable, the mismatch error of each individual
region may vary significantly with
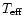 ,
as discussed
in Sect. 4.4.
The smallest mismatch errors from the H-line regions are of very much
the same magnitude as the errors of the best metal-line regions,
while at the same time H-line regions are never found among those
regions that give rise to the highest errors. A more detailed discussion
of the H-line regions is given in Sect. 4.5.
,
as discussed
in Sect. 4.4.
The smallest mismatch errors from the H-line regions are of very much
the same magnitude as the errors of the best metal-line regions,
while at the same time H-line regions are never found among those
regions that give rise to the highest errors. A more detailed discussion
of the H-line regions is given in Sect. 4.5.
As Fig. 3 shows, the global distribution
of mismatch errors scales approximately linearly with vsini.
In order to investigate this dependence more quantitatively for
individual spectral regions, those regions were selected that
contain exactly the same interval in wavelength
for all values of vsini.
This was repeated for the 5 values of
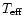 separately in order to
detect a possible further dependence on temperature.
separately in order to
detect a possible further dependence on temperature.
![\begin{figure}
\includegraphics[width=12cm]{fig_vsiniscal.eps}\end{figure}](/articles/aas/full/1999/19/h1521/Timg37.gif) |
Figure 4:
Normalised mismatch error
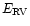 as a function of vsini,
plotted on a double logarithmic
scale. Different curves represent all spectral regions that contain
exactly the same interval in wavelength over the full range of vsini
for spectra with
as a function of vsini,
plotted on a double logarithmic
scale. Different curves represent all spectral regions that contain
exactly the same interval in wavelength over the full range of vsini
for spectra with
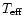 = 8000 K. Dotted lines represent
H-line regions.
The thick line depicts Eq. (1), its slope
representing a linear scaling of the error
between any two values of vsini
= 8000 K. Dotted lines represent
H-line regions.
The thick line depicts Eq. (1), its slope
representing a linear scaling of the error
between any two values of vsini |
A linear relation between the mismatch error from a given spectral region
and vsini, assuming the error is zero if vsini = 0,
can conveniently be expressed on a logarithmic scale:
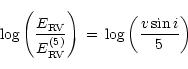 |
(1) |
with
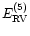 the mismatch error
at vsini = 5 kms-1 to which the errors for other vsiniare normalised.
Figure 4 shows the mismatch error for
the mismatch error
at vsini = 5 kms-1 to which the errors for other vsiniare normalised.
Figure 4 shows the mismatch error for
 = 8000 K
as a function of vsini for all 8 selected regions;
it also depicts Eq. (1). The double logarithmic
scale has the advantage that a linear dependence of the mismatch error on
vsini between any two vsini values is translated into
a connecting line with a gradient of unity, i.e. parallel to
Eq. (1).
= 8000 K
as a function of vsini for all 8 selected regions;
it also depicts Eq. (1). The double logarithmic
scale has the advantage that a linear dependence of the mismatch error on
vsini between any two vsini values is translated into
a connecting line with a gradient of unity, i.e. parallel to
Eq. (1).
As the plots in Fig. 4 are not significantly different
for different temperatures, we can draw the following conclusions from
all of them:
-
 increases monotonically with vsini in almost all
spectral regions,
partly because in a majority of the wavelength regions all individual mismatch
shifts actually increase monotonically, and partly because
increases monotonically with vsini in almost all
spectral regions,
partly because in a majority of the wavelength regions all individual mismatch
shifts actually increase monotonically, and partly because
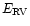 ,
by its very definition, is likely to keep on growing even if some of
the individual shifts do not.
The behaviour of the individual mismatch shifts themselves (monotonic or not)
can often be explained qualitatively in terms of the results of the
simple two-line study by
Verschueren ([1991]) (see Sect. 2.2), bearing in mind that
the distance between spectral lines in units of their width decreases
as rotational broadening increases.
In particular, in some spectral regions
where the mismatch error exhibits a maximum as a function
of vsini, one finds that the condition for a maximum is
indeed reached and passed at some vsini < 300 kms-1
and that all individual mismatch shifts decrease in absolute magnitude.
,
by its very definition, is likely to keep on growing even if some of
the individual shifts do not.
The behaviour of the individual mismatch shifts themselves (monotonic or not)
can often be explained qualitatively in terms of the results of the
simple two-line study by
Verschueren ([1991]) (see Sect. 2.2), bearing in mind that
the distance between spectral lines in units of their width decreases
as rotational broadening increases.
In particular, in some spectral regions
where the mismatch error exhibits a maximum as a function
of vsini, one finds that the condition for a maximum is
indeed reached and passed at some vsini < 300 kms-1
and that all individual mismatch shifts decrease in absolute magnitude.
- Almost all curves have at least one part where the increase is stronger
than linear and at least one part where it is less strong than linear.
Furthermore, for any step in vsini,
different spectral regions exhibit a large
range in slope around the linear value. Although rotational broadening
increases
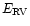 on average, the details of the blending
in each individual region determine the final outcome to a large extent.
on average, the details of the blending
in each individual region determine the final outcome to a large extent.
-
The vsini-dependence of the mismatch errors arising
from H-line regions does not seem any
different from that arising from the metal-line
regions. The reason is that mismatch errors in H-line regions
are caused solely by the blending metal lines (with some exception
occurring in the Balmer line region; see Sect. 4.5).
For a given vsini, the mismatch error
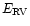 for
any given spectral region may vary considerably with the temperature
parameter
for
any given spectral region may vary considerably with the temperature
parameter
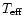 of the spectrum.
This is shown for vsini = 50 kms-1 in Fig. 5.
The following conclusions can be drawn:
of the spectrum.
This is shown for vsini = 50 kms-1 in Fig. 5.
The following conclusions can be drawn:
-
The mismatch errors of the majority of the spectral regions vary
monotononically with temperature, although the sign and the range
of the variations varies substantially from one region to the next.
Again, the details of the blending in each spectral region are the crucial
factor;
-
Spectral regions with a relatively weak dependence on temperature
also have a relatively small average
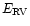 .
Average errors for these "best'' regions are
.
Average errors for these "best'' regions are 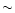 0.04, 0.4, 1, 1.5, 2 and
3 kms-1 for vsini = 5, 50, 100, 150, 200 and 300 kms-1,
respectively. Note that these "best'' regions are largely different ones
for different vsini; this seriously hampers the selection of
regions suitable for all spectra (see Sect. 5);
0.04, 0.4, 1, 1.5, 2 and
3 kms-1 for vsini = 5, 50, 100, 150, 200 and 300 kms-1,
respectively. Note that these "best'' regions are largely different ones
for different vsini; this seriously hampers the selection of
regions suitable for all spectra (see Sect. 5);
-
Some spectral regions have mismatch errors that vary up to a factor of 10
across the temperature range considered. Such large variations, however, do not
occur among H-line regions.
![\begin{figure}
\includegraphics[width=12cm]{fig_temp.eps}\end{figure}](/articles/aas/full/1999/19/h1521/Timg40.gif) |
Figure 5:
Mismatch error
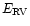 as a function of the different spectral regions
for 5 different temperatures: 1 = 7500 K, 2 = 8000 K, 3 = 8500 K,
4 = 9000 K and 5 = 9500 K. The rotational velocity is 50 kms-1in all cases. Spectral regions are indicated by the number of the continuum
window corresponding to their starting wavelength
(see Table 1).
Horizontal full lines indicate the length of a region if it is larger
than the distance between two consecutive continuum windows in
Table 1
as a function of the different spectral regions
for 5 different temperatures: 1 = 7500 K, 2 = 8000 K, 3 = 8500 K,
4 = 9000 K and 5 = 9500 K. The rotational velocity is 50 kms-1in all cases. Spectral regions are indicated by the number of the continuum
window corresponding to their starting wavelength
(see Table 1).
Horizontal full lines indicate the length of a region if it is larger
than the distance between two consecutive continuum windows in
Table 1 |
Figure 5 supports a comparison with the work of Fekel
([1985], [1999]),
who has derived accurate RVs for late B- and A-type stars that have
vsini < 50 kms-1. Fekel uses the MgII line at 4481 Å
(situated in our region No. 14-15) and the 5 FeII and TiII lines
between
4500 - 4525 Å (situated at the end of region No. 15-16
and at the beginning of No. 16-17).
Our error in region No. 14-15 (MgII) remains small
for vsini = 5 kms-1 but it increases drastically with
decreasing temperature for vsini = 50 kms-1(see Fig. 5). For that value of the rotation
the region is still reliable for early-A
spectra, but yields unacceptably high errors for mid- and late-A ones
owing to blending by lines which have a strong temperature dependence.
Incidentally, the mid and late A-type stars in Fekel's study all have
vsini < 15 kms-1 (Fekel 1999, private communication) which
helps to explain the relatively small errors he finds for those stars
using the MgII line.
Also for vsini > 50 kms-1, we find that
the MgII line yields relatively small errors for early A-type spectra only.
The other two regions which contain lines used by Fekel
are in fact among the very best, producing mismatch errors between
0.02 - 0.04 kms-1 for vsini = 5 kms-1
and between 0.2 - 0.4 kms-1for vsini = 50 kms-1 (depending on temperature).
However, since the maximum mismatch in temperature we have considered
spans only 2 temperature
sub-classes in either direction, our results indicate that allowing a
considerably larger mismatch, such as Fekel ([1985],
[1999]) employs, is not
without risk for vsini approaching 50 kms-1.
For vsini > 50 kms-1, our region No. 15-16 remains among
the best despite the blending which occurs shortward of Fekel's lines.
At that rotational velocity, region No. 16-17 behaves well only
in early A-type spectra, and produces
relatively high mismatch errors for cooler spectra owing to
a complex blend which affects most of Fekel's lines.
Owing to the much larger widths and strengths of the Hydrogen lines compared
to the metal lines in these early-type spectra,
spectral regions that contain H lines
require separate investigation. It is important to realize at the outset
that the mismatch errors of the 4 regions that contain just one H line
differ from zero only because of the
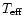 - and
logg-dependent blending with metal lines; the H line itself is
always isolated and symmetric.
On the one hand, mismatch errors arising from those 4 H-line regions
are expected to be smaller on average than those arising from
regions with only metal lines because the strong,
broad H line dampens extraneous contributions while not itself contributing
to the mismatch; smaller errors for H-line regions are
expected also because they have a much larger wavelength span
than metal-line regions and because some degree of cancelling of errors
always occurs (see Sect. 5.1).
On the other hand, some differences in the characteristics of the metal lines
(e.g. a difference in strength of an isolated line)
will yield (larger) mismatch shifts if those lines
occur on the inclined wings of a H-line profile;
in addition, differences in spectrum rectification may be an important
source of mismatch for these regions.
The nett effect cannot easily be predicted, though the distributions
given in Sect. 4.2 already showed that mismatch errors from H-line
regions lie well within the range found for metal-line regions.
- and
logg-dependent blending with metal lines; the H line itself is
always isolated and symmetric.
On the one hand, mismatch errors arising from those 4 H-line regions
are expected to be smaller on average than those arising from
regions with only metal lines because the strong,
broad H line dampens extraneous contributions while not itself contributing
to the mismatch; smaller errors for H-line regions are
expected also because they have a much larger wavelength span
than metal-line regions and because some degree of cancelling of errors
always occurs (see Sect. 5.1).
On the other hand, some differences in the characteristics of the metal lines
(e.g. a difference in strength of an isolated line)
will yield (larger) mismatch shifts if those lines
occur on the inclined wings of a H-line profile;
in addition, differences in spectrum rectification may be an important
source of mismatch for these regions.
The nett effect cannot easily be predicted, though the distributions
given in Sect. 4.2 already showed that mismatch errors from H-line
regions lie well within the range found for metal-line regions.
![\begin{figure}
\includegraphics[width=12cm]{fig_hlines.eps}\end{figure}](/articles/aas/full/1999/19/h1521/Timg41.gif) |
Figure 6:
Mismatch errors
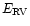 of the 5 H-line regions as a function of
spectral temperature for a rotational velocity of 150 kms-1.
The regions are: 1 = H14 - H8 (Balmer region), 2 = H
of the 5 H-line regions as a function of
spectral temperature for a rotational velocity of 150 kms-1.
The regions are: 1 = H14 - H8 (Balmer region), 2 = H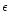 ,
3 = H ,
3 = H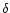 ,
4 = H ,
4 = H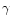 ,
5 = H ,
5 = H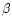 .
Dashed lines indicate a change in length of the actual wavelength interval,
which occurs when a small adjacent metal-line region merges with
the H-line region (see Sect. 3.4) .
Dashed lines indicate a change in length of the actual wavelength interval,
which occurs when a small adjacent metal-line region merges with
the H-line region (see Sect. 3.4) |
Figure 6 shows the mismatch errors
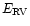 of the
5 H-line regions for the 5 temperatures considered, and for vsini= 150 kms-1. From this and similar plots for different vsiniwe conclude:
of the
5 H-line regions for the 5 temperatures considered, and for vsini= 150 kms-1. From this and similar plots for different vsiniwe conclude:
-
Mismatch errors arising from the regions containing
H
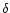 ,
H
,
H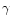 and H
and H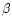 (labelled 3, 4 and 5) are
relatively small; they show no
common dependence on temperature for any vsini, and in that sense
they behave similarly to the metal-line regions.
Since it is the detailed content of the
metal lines in the H-line regions that determines the mismatch shifts,
the addition of adjacent small wavelength regions to a H-line region
(see the dashed lines) can have a non-negligible effect;
(labelled 3, 4 and 5) are
relatively small; they show no
common dependence on temperature for any vsini, and in that sense
they behave similarly to the metal-line regions.
Since it is the detailed content of the
metal lines in the H-line regions that determines the mismatch shifts,
the addition of adjacent small wavelength regions to a H-line region
(see the dashed lines) can have a non-negligible effect;
-
For vsini < 50 kms-1, the situation for region 2
containing H
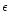 is similar to that of the 3 regions discussed above.
For larger rotational velocities, however, mismatch is dominated by the
blending with the CaII H line, though in
mid- or late-A- spectra the K line also blends with the
far wing of H
is similar to that of the 3 regions discussed above.
For larger rotational velocities, however, mismatch is dominated by the
blending with the CaII H line, though in
mid- or late-A- spectra the K line also blends with the
far wing of H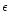 ;
both CaII lines vary markedly with temperature, growing from a very weak
line at late B to strong and broad lines at early F.
The resulting mismatch errors show a very strong temperature
dependence and are relatively high for mid- and late-A spectra.
This particular type of blending occurs only in the H
;
both CaII lines vary markedly with temperature, growing from a very weak
line at late B to strong and broad lines at early F.
The resulting mismatch errors show a very strong temperature
dependence and are relatively high for mid- and late-A spectra.
This particular type of blending occurs only in the H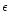 spectral region;
spectral region;
-
For small vsini, the situation for region 1 containing the
Balmer-series limit (H14 - H8) is again similar to that of the other
H-line regions. For larger rotational velocities, the errors remain small
for early- and mid-A spectra but become relatively large for late-A ones.
We suggest the following tentative explanation.
At larger vsini the mismatch is dominated by the seven
mutually blended H lines; those lines become broader with
increasing temperature, reaching a maximum at early A. Their blending
therefore alters substantially with temperature for
the late A-type spectra, while reaching a more stable, almost
temperature-independent, configuration for the early A-type spectra.
If that mechanism is indeed the dominant one, and if other factors remained
equal, we might expect mismatch
errors for that spectral region to increase again for B-type stars,
where the H lines become more narrow with increasing temperature.


Up: Accuracy of radial-velocity measurements
Copyright The European Southern Observatory (ESO)
![]() of the individual spectral regions.
We recall that
each is defined as the maximum mismatch shift (in absolute
value) out of the 14 different mismatch cases
(two steps of
of the individual spectral regions.
We recall that
each is defined as the maximum mismatch shift (in absolute
value) out of the 14 different mismatch cases
(two steps of ![]() 250 K in
250 K in
![]() and one step of
and one step of ![]() 0.2 dex
in logg; see Sect. 3.2). We discuss these results for the 30
main-grid spectra considered,
i.e. for the 5 values of temperature, 1 of surface gravity,
and 6 of rotational velocity, representing the rotating
A-type main-sequence stars (see Sect. 3.3).
First, in Sect. 4.1, we look in more detail at the individual mismatch shifts
arising from the 14 different mismatch cases.
0.2 dex
in logg; see Sect. 3.2). We discuss these results for the 30
main-grid spectra considered,
i.e. for the 5 values of temperature, 1 of surface gravity,
and 6 of rotational velocity, representing the rotating
A-type main-sequence stars (see Sect. 3.3).
First, in Sect. 4.1, we look in more detail at the individual mismatch shifts
arising from the 14 different mismatch cases.
![]() ,
logg) of the mismatch grid
as chosen in Sect. 3.2 needs to be sufficiently small
to sample properly the mismatch error
,
logg) of the mismatch grid
as chosen in Sect. 3.2 needs to be sufficiently small
to sample properly the mismatch error
![]() as a function
of
as a function
of
![]() and
and
![]() .
We are satisfied that the latter requirement
has in fact been met because a simple four-parameter model
(
.
We are satisfied that the latter requirement
has in fact been met because a simple four-parameter model
(
![]() )
fits the 14 mismatch shifts fairly well for most spectral
regions in all main-grid spectra.
We also found that the maximum mismatch shift, i.e. the mismatch error
)
fits the 14 mismatch shifts fairly well for most spectral
regions in all main-grid spectra.
We also found that the maximum mismatch shift, i.e. the mismatch error
![]() ,
for
,
for
![]() K (i.e. for 14 mismatch cases)
is twice that for
K (i.e. for 14 mismatch cases)
is twice that for
![]() K (i.e. for 8 mismatch cases),
with an rms deviation less than 0.5 for all
30 main-grid spectra and for all spectral regions.
K (i.e. for 8 mismatch cases),
with an rms deviation less than 0.5 for all
30 main-grid spectra and for all spectral regions.
![]() from the different spectral regions.
A Kolmogorov-Smirnov test shows that, for a given rotational velocity,
the hypothesis that the distributions for the 5 different temperatures
are identical cannot be rejected,
although the relatively small
number of regions must influence that result.
We can therefore combine the results for all
from the different spectral regions.
A Kolmogorov-Smirnov test shows that, for a given rotational velocity,
the hypothesis that the distributions for the 5 different temperatures
are identical cannot be rejected,
although the relatively small
number of regions must influence that result.
We can therefore combine the results for all
![]() ;
Fig. 3 shows the distributions for the 6 values
of vsini. It is immediately apparent that a large range in
;
Fig. 3 shows the distributions for the 6 values
of vsini. It is immediately apparent that a large range in
![]() exists among the different regions at any given vsini:
the 10% highest errors are on average about a factor 20 larger
than the 10% smallest ones.
exists among the different regions at any given vsini:
the 10% highest errors are on average about a factor 20 larger
than the 10% smallest ones.
![\begin{figure}
\includegraphics[width=20cm]{fig_distr.eps}\end{figure}](/articles/aas/full/1999/19/h1521/Timg36.gif)
![]() for different temperatures
are indistinguishable, the mismatch error of each individual
region may vary significantly with
for different temperatures
are indistinguishable, the mismatch error of each individual
region may vary significantly with
![]() ,
as discussed
in Sect. 4.4.
The smallest mismatch errors from the H-line regions are of very much
the same magnitude as the errors of the best metal-line regions,
while at the same time H-line regions are never found among those
regions that give rise to the highest errors. A more detailed discussion
of the H-line regions is given in Sect. 4.5.
,
as discussed
in Sect. 4.4.
The smallest mismatch errors from the H-line regions are of very much
the same magnitude as the errors of the best metal-line regions,
while at the same time H-line regions are never found among those
regions that give rise to the highest errors. A more detailed discussion
of the H-line regions is given in Sect. 4.5.
![]() separately in order to
detect a possible further dependence on temperature.
separately in order to
detect a possible further dependence on temperature.
![\begin{figure}
\includegraphics[width=12cm]{fig_vsiniscal.eps}\end{figure}](/articles/aas/full/1999/19/h1521/Timg37.gif)
![]() for
any given spectral region may vary considerably with the temperature
parameter
for
any given spectral region may vary considerably with the temperature
parameter
![]() of the spectrum.
This is shown for vsini = 50 kms-1 in Fig. 5.
The following conclusions can be drawn:
of the spectrum.
This is shown for vsini = 50 kms-1 in Fig. 5.
The following conclusions can be drawn:
![\begin{figure}
\includegraphics[width=12cm]{fig_temp.eps}\end{figure}](/articles/aas/full/1999/19/h1521/Timg40.gif)
![]() - and
logg-dependent blending with metal lines; the H line itself is
always isolated and symmetric.
On the one hand, mismatch errors arising from those 4 H-line regions
are expected to be smaller on average than those arising from
regions with only metal lines because the strong,
broad H line dampens extraneous contributions while not itself contributing
to the mismatch; smaller errors for H-line regions are
expected also because they have a much larger wavelength span
than metal-line regions and because some degree of cancelling of errors
always occurs (see Sect. 5.1).
On the other hand, some differences in the characteristics of the metal lines
(e.g. a difference in strength of an isolated line)
will yield (larger) mismatch shifts if those lines
occur on the inclined wings of a H-line profile;
in addition, differences in spectrum rectification may be an important
source of mismatch for these regions.
The nett effect cannot easily be predicted, though the distributions
given in Sect. 4.2 already showed that mismatch errors from H-line
regions lie well within the range found for metal-line regions.
- and
logg-dependent blending with metal lines; the H line itself is
always isolated and symmetric.
On the one hand, mismatch errors arising from those 4 H-line regions
are expected to be smaller on average than those arising from
regions with only metal lines because the strong,
broad H line dampens extraneous contributions while not itself contributing
to the mismatch; smaller errors for H-line regions are
expected also because they have a much larger wavelength span
than metal-line regions and because some degree of cancelling of errors
always occurs (see Sect. 5.1).
On the other hand, some differences in the characteristics of the metal lines
(e.g. a difference in strength of an isolated line)
will yield (larger) mismatch shifts if those lines
occur on the inclined wings of a H-line profile;
in addition, differences in spectrum rectification may be an important
source of mismatch for these regions.
The nett effect cannot easily be predicted, though the distributions
given in Sect. 4.2 already showed that mismatch errors from H-line
regions lie well within the range found for metal-line regions.
![]() of the
5 H-line regions for the 5 temperatures considered, and for vsini= 150 kms-1. From this and similar plots for different vsiniwe conclude:
of the
5 H-line regions for the 5 temperatures considered, and for vsini= 150 kms-1. From this and similar plots for different vsiniwe conclude: