

Up: Period-Luminosity-Colour distribution and classification LPVs
Subsections
The fitted distributions of period, magnitude and colour correspond
to the following PLC relations (where the error bars correspond to
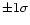 deviations, as estimated using Monte Carlo simulations):
deviations, as estimated using Monte Carlo simulations):
- Group 1:
![$\sigma_M\, =\, 0.63_{[\pm 0.13]}$](/articles/aas/full/1999/19/ds8586/img49.gif)
- Group 2:
![$\sigma_M\, =\, 0.32_{[\pm 0.17]}$](/articles/aas/full/1999/19/ds8586/img51.gif)
- Group 3:
![$\sigma_M\, =\, 0.50_{[\pm 0.08]}$](/articles/aas/full/1999/19/ds8586/img53.gif)
- Group 4:
![$\sigma_M\, =\, 0.48_{[\pm 0.21]}$](/articles/aas/full/1999/19/ds8586/img55.gif) .
.
The coefficients of the relation found for Group 4 are obviously very
uncertain. This is not surprising, in view of the small number of stars
(14), their small dispersion, and the number of parameters to
estimate. For Groups 1, 2 and 4, the error bars on the zero point are
relatively large; this is due to the fact that the means of the three
variables are far from zero, and thus any slope uncertainty rebounds
magnified on the zero point.
The tridimensional model distributions may be projected onto the
period-luminosity plane. The elliptic-looking lines shown in Fig. 5
are the projections of the isoprobability contours that, in the mean
PLC plane, correspond to a 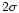 deviation. The offset between
the data and the model populations is due to the sampling bias, which
is suppressed by the LM algorithm (see Appendix A for details).
Then, Period-luminosity relations, liable to be compared to the ones
observed in the Magellanic Clouds, are derived by means of a linear
least-squares fit to the contours. Monte-Carlo simulations, as well as
analytic computations, have shown that this is equivalent to a fit onto the
projected population itself. Finally, the error bars of the coefficients
are estimated, for each group, by applying the standard least-squares
procedure to a simulated unbiased sample (thus they may be directly compared
to the error bars usually given for the LMC stars).
deviation. The offset between
the data and the model populations is due to the sampling bias, which
is suppressed by the LM algorithm (see Appendix A for details).
Then, Period-luminosity relations, liable to be compared to the ones
observed in the Magellanic Clouds, are derived by means of a linear
least-squares fit to the contours. Monte-Carlo simulations, as well as
analytic computations, have shown that this is equivalent to a fit onto the
projected population itself. Finally, the error bars of the coefficients
are estimated, for each group, by applying the standard least-squares
procedure to a simulated unbiased sample (thus they may be directly compared
to the error bars usually given for the LMC stars).
The results are the following:
- Group 1:
- Group 2:
- Group 3:
- Group 4:
It may be noticed that Groups 2 and 3 have similar mean magnitudes.
The same holds for Groups 1 and 4.
![\begin{figure}\includegraphics[width=12cm]{ds8586f5.eps}\end{figure}](/articles/aas/full/1999/19/ds8586/Timg60.gif) |
Figure 5:
PL calibrated distributions: individual data and projected
model distributions (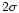 isoprobability contours in the mean PLC
plane). The Mira strip of the LMC is also shown (thick lines)
isoprobability contours in the mean PLC
plane). The Mira strip of the LMC is also shown (thick lines) |
From a sample of 29 O-rich Miras of the Large Magellanic Cloud with period
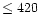 days, Feast et al. ([1989]) derived the following relation
(were the error bars correspond to
days, Feast et al. ([1989]) derived the following relation
(were the error bars correspond to 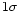 deviations):
deviations):
assuming a distance modulus of 18.55.
Based on a sample of more than a hundred Oxygen-rich Miras of the LMC, the
solution of Hughes & Wood ([1990]) is, under the same assumptions:
From a sample of 79 Miras, unfortunately including a significant number of
Carbon stars, Hughes ([1993]) derived:
Obviously, the slopes are significantly different from that of any Galactic
PL relation found above. Such a difference was also observed between the LMC
and Globular Clusters stars by Menzies & Whitelock ([1985]).
It cannot be due to the well-known steepening of the PL relation at periods
larger than 420 days, i.e. relatively high mass (Feast et al.
[1989]), since only a very few sample stars may be concerned.
The first possible explanation is that the so-called Miras of the LMC
include, in fact, a significant number of SRb semiregulars, especially at
"short'' periods. Indeed, for the outer galaxies, the observers use to
call "Miras'' the LPVs with an amplitude larger than a given threshold
(e.g. 0.9 mag in I), corresponding to the maximum amplitude of SRa stars
according to the GCVS. This criterium is obviously not sufficient and the
slope of the so-called LMC "Mira'' strip should then be intermediary
between our Groups 1 and 2. A second explanation of the slope discrepancy is
that the shorter-period "Miras'' in the LMC include a population
more-or-less equivalent to our Group 4, i.e. metal-deficient with a mean
mass similar to or lower than the one of the main population. This, too,
would lead to a shallower global PL relation. The existence of such a
population had been suggested by Wood et al. ([1985]) and Hughes et al. ([1991]). Of course, these two explanations do not exclude
each other.
It is also worth noting that the PL slopes of Groups 2 and 3 are much smaller
than the one of Group 1 (Miras), and similar to the one of the
evolutionary tracks (-1.67), derived by Bedding & Zijlstra
([1998]) from the works of Whitelock ([1986]) and
Vassiliadis & Wood ([1993]).
Moreover, in Group 2 as well as in Group 3, the proportion of SRb's (as
defined by the GCVS) decreases towards longer periods: at P> 200 days,
they represent less than 25% of the stars of these groups, while Miras
(GCVS) amount to 45% for Group 2 and 65% for Group 3.
All of this indicates that, in each population, the sequence of SRb
Semiregulars corresponds to an evolutionary sequence towards the Mira
instability strip.
In the same way as in the preceding subsection, a linear fit to the
projected model distributions (see Fig. 6) yields the following
period-colour relations:
- Group 1:
- Group 2:
- Group 3:
- Group 4:
The difference of slope between Groups 2 and 3 is (qualitatively) consistent
with the differences of mass and metallicity expected from the kinematics.
Indeed, the larger mass of Group 3 stars yields significantly higher
temperatures and thus a larger {
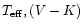 } slope, while the
moderate metallicity difference has only a small influence (Bessell et al.
[1989,1998]). This is due to the behaviour of the TiO lines in
this temperature range.
} slope, while the
moderate metallicity difference has only a small influence (Bessell et al.
[1989,1998]). This is due to the behaviour of the TiO lines in
this temperature range.
On the other hand, the much larger slope of Group 1 may be explained by
a difference of pulsation mode, consistently with the larger mean period.
Indeed, the period of a lower-order mode must be more sensitive to the
temperature (see, e.g., Barthès [1998]).
![\begin{figure}\includegraphics[width=12cm]{ds8586f6.eps}\end{figure}](/articles/aas/full/1999/19/ds8586/Timg73.gif) |
Figure 6:
PC calibrated distributions: individual data and
projected model distributions |
The calibration results in the Luminosity-Colour plane are shown in Fig. 7.
As explained in the Appendix A, the offset and the difference of width
between the data distributions and the projected 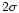 contours are
effects of the projection and of the sampling bias.
A linear fit to the contours yields the following luminosity-colour
relations:
contours are
effects of the projection and of the sampling bias.
A linear fit to the contours yields the following luminosity-colour
relations:
- Group 1:
- Group 2:
- Group 3:
- Group 4:
As in the preceding subsection, the difference of slope
between Groups 2 and
3 is easily explained by the temperature-dependence of the
{
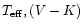 } slope, which is little sensitive to moderate
metallicity variations.
} slope, which is little sensitive to moderate
metallicity variations.
![\begin{figure}\includegraphics[width=12cm]{ds8586f7.eps}\end{figure}](/articles/aas/full/1999/19/ds8586/Timg78.gif) |
Figure 7:
LC calibrated distributions: individual data and
projected model distributions |
Once the distances have been calibrated, it is possible to check the
distribution of the sample stars with respect to the de-reddened J-K
index. The results are shown in Fig. 8, together with the raw data.
The J-K Period-Colour distribution appears similar to the V-K one.
The scattering, also existing in the raw data, makes the PC relation more
difficult to see. It is due to the smaller number of stars in the J data
set, and probably also to the peculiar sensitivity of this colour index to
the surface gravity and extension of the envelope (Bessell et al.
[1989,1998]).
A linear least-squares fit to the de-reddened data (excluding a few
obviously misclassified stars, namely two having
(J-K)0 > 2 and two having
(J-K)0 < 0.6) yields:
- Group 1 (86 stars):
- Group 2 (63 stars):
- Group 3 (91 stars):
- Group 4 (12 stars):
These fit relations are probably slightly biased, and thus should be
shifted by a certain amount so as to represent the whole populations.
Contrary to what was found with V-K, the relations of Groups 2 and 3
cannot be reliably distinguished here. This may be due to the crossing-over
of the iso-metallicity curves in the {
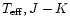 } diagram: the
effects of the differences of temperature and metallicity between the two
groups tend to compensate each-other (Bessell et al. [1989,1998]).
} diagram: the
effects of the differences of temperature and metallicity between the two
groups tend to compensate each-other (Bessell et al. [1989,1998]).
![\begin{figure}\begin{tabular}{c}
\includegraphics[width=12cm]{ds8586f8a.eps}\\
\includegraphics[width=12cm]{ds8586f8b.eps}\end{tabular}\end{figure}](/articles/aas/full/1999/19/ds8586/Timg86.gif) |
Figure 8:
J-K versus Period distribution of sample stars: raw ( top)
and dereddened ( bottom) indices. Two stars with J-K > 2 are not
shown |
Based on 29 Oxygen Miras, the relation found by Feast et al. ([1989])
for the LMC is:
From a sample of 21 stars, Hughes ([1993]) derived:
As for the PL relation, we find a significant discrepancy between the Miras
in the LMC and the ones in the solar neighbourhood. Since, in J-K as well
as in V-K, Group 4 is approximately aligned with Group 1, and thus
metal-deficient Miras of the LMC should not significantly influence its PC
relation, it seems that, as suggested in Sect. 5.2, we are actually
encountering a problem of misclassification of the LPVs in the outer
galaxies. This, of course, does not preclude the existence of a
metal-deficient population which would further influence the PL relation.
The LC relations yielded by a linear least-squares fit to the calibrated
and de-reddened data are:
- Group 1:
- Group 2:
- Group 3:
- Group 4:
We remind that these fit relations are subject to sampling bias, and thus
should be significantly shifted downwards, so as to represent the whole
population (see Appendix A).
In view of the error bars, the slope of Group 3 may be the same as the
one of Groups 1 and 2, which is what is expected from AGB evolutionary
models. This supports our interpretation of the slope differences found
in V-K (Sect. 5.4). The slope of Group 4 is, once again, not
reliable.
![\begin{figure}\includegraphics[width=12cm]{ds8586f9.eps}\end{figure}](/articles/aas/full/1999/19/ds8586/Timg99.gif) |
Figure 9:
Magnitude versus (J-K)0 distribution of the sample stars,
deduced from the luminosity calibration |


Up: Period-Luminosity-Colour distribution and classification LPVs
Copyright The European Southern Observatory (ESO)
![\begin{eqnarray*}M_K & = -1.07_{[\pm 0.50]} \log P & - 0.37_{[\pm 0.13]} (V-K)_0 \\
& & - 1.49_{[\pm 0.72]}
\end{eqnarray*}](/articles/aas/full/1999/19/ds8586/img48.gif)
![\begin{eqnarray*}M_K & = -0.37_{[\pm 0.94]} \log P & -0.42_{[\pm 0.24]} (V-K)_0\\
& & -3.23_{[\pm 1.35]}
\end{eqnarray*}](/articles/aas/full/1999/19/ds8586/img50.gif)
![\begin{eqnarray*}M_K & = -1.69_{[\pm 0.54]} \log P & -0.16_{[\pm 0.14]} (V-K)_0\\
& & -2.53_{[\pm 0.78]}
\end{eqnarray*}](/articles/aas/full/1999/19/ds8586/img52.gif)
![\begin{eqnarray*}M_K & = -0.81_{[\pm 1.72]} \log P & -0.09_{[\pm 0.45]} (V-K)_0\\
& & -4.76_{[\pm 2.48]}
\end{eqnarray*}](/articles/aas/full/1999/19/ds8586/img54.gif)
![\begin{eqnarray*}M_K & = -1.07_{[\pm 0.50]} \log P & - 0.37_{[\pm 0.13]} (V-K)_0 \\
& & - 1.49_{[\pm 0.72]}
\end{eqnarray*}](/articles/aas/full/1999/19/ds8586/img48.gif)
![\begin{eqnarray*}M_K & = -0.37_{[\pm 0.94]} \log P & -0.42_{[\pm 0.24]} (V-K)_0\\
& & -3.23_{[\pm 1.35]}
\end{eqnarray*}](/articles/aas/full/1999/19/ds8586/img50.gif)
![\begin{eqnarray*}M_K & = -1.69_{[\pm 0.54]} \log P & -0.16_{[\pm 0.14]} (V-K)_0\\
& & -2.53_{[\pm 0.78]}
\end{eqnarray*}](/articles/aas/full/1999/19/ds8586/img52.gif)
![\begin{eqnarray*}M_K & = -0.81_{[\pm 1.72]} \log P & -0.09_{[\pm 0.45]} (V-K)_0\\
& & -4.76_{[\pm 2.48]}
\end{eqnarray*}](/articles/aas/full/1999/19/ds8586/img54.gif)
![\begin{figure}\includegraphics[width=12cm]{ds8586f5.eps}\end{figure}](/articles/aas/full/1999/19/ds8586/Timg60.gif)
![]() days, Feast et al. ([1989]) derived the following relation
(were the error bars correspond to
days, Feast et al. ([1989]) derived the following relation
(were the error bars correspond to ![]() deviations):
deviations):
![]() contours are
effects of the projection and of the sampling bias.
A linear fit to the contours yields the following luminosity-colour
relations:
contours are
effects of the projection and of the sampling bias.
A linear fit to the contours yields the following luminosity-colour
relations:
![]() } slope, which is little sensitive to moderate
metallicity variations.
} slope, which is little sensitive to moderate
metallicity variations.
![]() } diagram: the
effects of the differences of temperature and metallicity between the two
groups tend to compensate each-other (Bessell et al. [1989,1998]).
} diagram: the
effects of the differences of temperature and metallicity between the two
groups tend to compensate each-other (Bessell et al. [1989,1998]).
![\begin{figure}\begin{tabular}{c}
\includegraphics[width=12cm]{ds8586f8a.eps}\\
\includegraphics[width=12cm]{ds8586f8b.eps}\end{tabular}\end{figure}](/articles/aas/full/1999/19/ds8586/Timg86.gif)
![\begin{figure}\includegraphics[width=12cm]{ds8586f9.eps}\end{figure}](/articles/aas/full/1999/19/ds8586/Timg99.gif)