SIPA1 consists of 200 stars, including 97 FK5 stars and 103 FK5 Extension
stars with ![]() . To determine the systematic errors
of SIPA1, 199 common stars between SIPA1 and Hipparcos catalogs were used. The
positions of Hipparcos stars were reduced to the observational epoch of SIPA1 and
the difference
. To determine the systematic errors
of SIPA1, 199 common stars between SIPA1 and Hipparcos catalogs were used. The
positions of Hipparcos stars were reduced to the observational epoch of SIPA1 and
the difference ![]() were obtained in the sense
of SIPA1 - Hipparcos, which are shown in Figs. 1a,b. The systematic
differences as a function of right ascension,
were obtained in the sense
of SIPA1 - Hipparcos, which are shown in Figs. 1a,b. The systematic
differences as a function of right ascension, ![]() and
and ![]() ,are negligible.
,are negligible.
![\begin{figure}
\includegraphics [width=7.8cm]{MS8303f2.eps}
\end{figure}](/articles/aas/full/1999/16/ds8303/Timg14.gif) |
Figure 2:
The difference |
The adopted values of latitude and instrument zenith
distance in the reduction of SIPA1 are based on the FK5 system. As is well known, the FK5
catalog, especially the FK5 Extension stars, have zonal systematic difference
relative to the Hipparcos catalog. The difference ![]() between the SIPA1
input catalog, which consists of FK5 and FK5 Extension stars, and the Hipparcos
catalog at the epoch of SIPA1 observations are shown in Fig. 2. The systematic
errors of FK5 may be introduced into SIPA1 in the following form [, (Li et al.
1983)]:
between the SIPA1
input catalog, which consists of FK5 and FK5 Extension stars, and the Hipparcos
catalog at the epoch of SIPA1 observations are shown in Fig. 2. The systematic
errors of FK5 may be introduced into SIPA1 in the following form [, (Li et al.
1983)]:
| (1) |
| (2) |
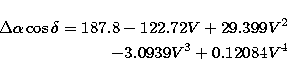 |
||
| (3) |
Copyright The European Southern Observatory (ESO)