If the above conditions are not satisfied one can envisage an alternative scenario where the key role is instead played by the balance between the cooling and heating processes. This would be favored if the emitting region occupies the entire shell volume rather than the narrow region associated with a planar shock.
An immediate prediction is that the typical energy of the emitting
electrons is mildly relativistic, and the main radiation process is
quasi-thermal Comptonization. This also implies the existence of a
characteristic observed frequency of a few MeV, controlled by the
feedback introduced by the effect of e![]() pair production.
pair production.
Let us assume that the heating process for a typical electron lasts
for the duration of the shell-shell interaction, ![]() . The maximum amount of energy given to a single lepton,
. The maximum amount of energy given to a single lepton,
![]() , corresponds to a total average
heating rate
, corresponds to a total average
heating rate ![]() . The
characteristic electron energy is given by balancing
. The
characteristic electron energy is given by balancing ![]() and
and ![]() , i.e.:
, i.e.:
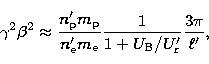 |
(1) |
The small energy of the emitting particles implies:
1) the synchrotron emission is self-absorbed. It peaks at a comoving
frequency ![]() Hz.
Hz.
2) the main radiation mechanism is multiple Compton scattering and the self-absorbed synchrotron emission is the source of soft seed photons.
If one defines a generalized Comptonization parameter ![]() , the ratio of the Compton to the
synchrotron powers can then be approximated by
, the ratio of the Compton to the
synchrotron powers can then be approximated by ![]() , and thus in
order to emit a Compton comoving luminosity
, and thus in
order to emit a Compton comoving luminosity ![]() erg s-1, y must be
erg s-1, y must be ![]() . With
this value of y, and
. With
this value of y, and ![]() , the Comptonized high energy spectrum
has a
, the Comptonized high energy spectrum
has a ![]() shape, while the relatively modest optical
depth prevents a strong Wien peak to form. Therefore, very
schematically, the resulting observed spectrum would extend between
shape, while the relatively modest optical
depth prevents a strong Wien peak to form. Therefore, very
schematically, the resulting observed spectrum would extend between
![]() and
and ![]() , with
, with ![]() const.
const.
The spectrum of a single shell will rapidly evolve: after the observed acceleration time, particles cool on a similar timescale, while the Comptonization spectrum steepens and the power decreases. In the time integrated emission any Wien hump and/or feature in the spectrum of individual shells will be smoothed out. The power-law continuum, if typical of all shells, would instead be preserved.
The e![]() pair production process can play a crucial role. This
would both increase the optical depth and act as a thermostat, by
maintaining the temperature in a narrow range. Additional pairs will
be also produced outside the shell region, increasing the lepton
content of the surrounding medium. The maximum equilibrium
temperature in steady sources in pair equilibrium with
pair production process can play a crucial role. This
would both increase the optical depth and act as a thermostat, by
maintaining the temperature in a narrow range. Additional pairs will
be also produced outside the shell region, increasing the lepton
content of the surrounding medium. The maximum equilibrium
temperature in steady sources in pair equilibrium with ![]() between 10 and 103 is of the order 30-300 keV
([Svensson 1984]). Note that additional pairs will be also produced
outside the shell region, increasing the lepton content of the
surrounding medium.
between 10 and 103 is of the order 30-300 keV
([Svensson 1984]). Note that additional pairs will be also produced
outside the shell region, increasing the lepton content of the
surrounding medium.
We conclude that an "effective'' temperature ![]() keV and
keV and
![]() dominated by pairs, can be a consistent solution giving
dominated by pairs, can be a consistent solution giving
![]() .
.
Copyright The European Southern Observatory (ESO)