2 General constraints

  We here prefer to discuss the implications of detecting an iron line during the X-ray afterglow of a generic burst, without referring in particular to the two cases mentioned in the introduction. Let us therefore assume that the flux of the X-ray afterglow is of the order of 10^-13 erg cm^-2 s^-1, and assume a redshift of z=1. To be visible during the X-ray afterglow emission, the emission line should have a comparable flux, $F_{\rm Fe}=10^{-13}F_{\rm Fe,-13}$ erg cm^-2 s^-1. This in itself constrains both the amount of line-emitting matter and the size of the emitting region.

2.1 Limit to the size

Assume for simplicity that the emitting region is a homogeneous spherical shell at a distance R from the $\gamma-$ray burst, with a width $\Delta R\le R$.The fluence of the emission line cannot exceed the absorbed ionizing fluence $q{\cal F}$ (where ${\cal F}$ is the total GRB fluence and q is the fraction of it which is absorbed and reprocessed into the line). The observed duration of the emission line cannot be shorter than the light crossing time of the region R/c. From this we obtain the limit

$$R\, <3\, \ 10^{18}\,{q\,{\cal F}_{-5}\over F_{\rm Fe,-13}}\quad {\rm cm}.$$ (1)

Since q is at most $\sim 0.03$, the emitting region is very compact, ruling out emission from interstellar matter, even assuming the large densities appropriate for star forming regions. We would like to stress that the above limit is independent of the variability of the line flux.

2.2 Limit to the mass

The total line photons produced at 6.4-6.9 keV in $10^5\, t_5$seconds, for a GRB located at z=1, are $\sim 3\ 10^{57}\,F_{\rm Fe,-13}\, t_5$. Assuming that each iron atom produces k line photons, this corresponds to $\sim 150\,F_{\rm Fe,-13}\,t_5/k \, M_\odot$ of iron. The parameter k depends on the details of the assumed scenario, but we can set some general limits. Assume in fact that each iron atom can emit photons only when illuminated by an ionizing flux, which is provided by the burst itself or by the high energy tail of the afterglow emission. Since the burst radiation has enough power to photoionize all the matter in the vicinity of the progenitor (see e.g. Boettcher et al. 1999), line photons will be emitted only through the recombination process. But even if we assume that the recombination is instantaneous, the value of the parameter k will not be larger than the total number of photoionizations an ion can undergo during the burst and/or the afterglow. For iron K-shell electrons, with cross section $\sigma_{K}=1.2\ 10^{-20}$ cm² we have:

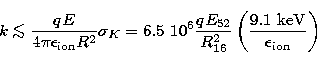$$k\mathrel{\mathchoice {\vcenter{\offinterlineskip\halign{\hf... ...2_{16}} \left({9.1\ {\rm keV} \over \epsilon_{\rm ion}}\right)$$ (2)

where E is the total energy emitted by the burst and/or afterglow and $\epsilon_{\rm ion}$ the energy of a single ionizing photon. This upper limit on k translates in a lower limit on the iron mass:

$$M_{\rm Fe} \mathrel{\mathchoice {\vcenter{\offinterlineskip\... ... 10^{-5} F_{\rm Fe,-13} t_5 {R_{16}^2 \over q E_{52}}\ M_\odot$$ (3)

which, for a solar iron abundance, yields a total mass , i.e. a third of a solar mass for $q \sim 0.03$.

Even if these numbers apparently do not rule out reverberation from a molecular cloud (Ghisellini et al. 1999; Mészáros & Ress 1998), we remark that the recombination time has been assumed negligible in the above discussion. At densities typical of molecular clouds the recombination time is larger than the burst duration and the value of k cannot exceed 12, set by the photoelectric yield of the iron atom (e.g. Boettcher et al. 1999).

2.3 Limit on geometry and isotropy

Optical afterglow emission has been observed in about half the $\gamma$-ray burst events for which the X-ray afterglow has been detected. In particular, the optical afterglow of GRB 970508 lasted for hundreds of days (Galama et al. 1998). If the iron line emitting region were spherically symmetric, it would inevitably stop the fireball and the usual relatively slow transformation of bulk kinetic energy into radiation could not take place. For this reason it is necessary to assume some special geometry of the iron line emitting material, which has not to interfere with the observed optical afterglow. In other words, this region cannot be located along our line of sight, but, on the other hand, it has to be illuminated by the burst emission, in order to produce the iron line feature (e.g. a torus surrounding the central region, or a bicone). Therefore we conclude that the iron line feature is a powerful tool to know how isotropic the burst emission is.