The essential assumption of Fermi-type shock acceleration is that
particles are deflected elastically in the local fluid frame on
either side of the shock, so that upon recrossing upstream after an
excursion downstream, say, they will have a net average energy gain.
For particles of Lorentz factor ![]() , this energy
gain can be expressed as
, this energy
gain can be expressed as
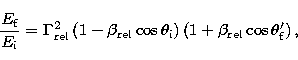 |
(1) |
Kinematics require that the second factor in parentheses in Eq. (1) be greater than 1. In the initial shock crossing, ![]() is isotropically distributed, and we do find
is isotropically distributed, and we do find ![]() .For physically realistic deflection processes upstream, however,
it can be shown that for all subsequent shock crossings,
.For physically realistic deflection processes upstream, however,
it can be shown that for all subsequent shock crossings, ![]() , so that we typically have
, so that we typically have ![]() (Gallant & Achterberg 1998, 1999).
(Gallant & Achterberg 1998, 1999).
Copyright The European Southern Observatory (ESO)