

Up: Temporal evolution of the
A visual inspection of the BATSE catalog of multiple-peaked time histories reveals that
peaks usually have about the same duration at the beginning of the burst as near the
end of the burst. Our aim is to characterize and measure the pulse shape as a function
of arrival time. The aligned peak method measures the average pulse temporal
structure, each burst contributes to the average by aligning the largest peak
([Mitrofanov 1997]).
We used all 53 bursts from the BATSE 4B Catalog that were longer than 20 s and brighter
than 5 photons s-1 cm-2. Each burst must have at least one peak, as
determined by a peak-finding algorithm (similar to
[Li & Fenimore 1996]),
in each third of its
duration. The largest peak in each third was normalized to unity and a shifted in time,
bringing the largest peaks of all bursts into common alignment. This method was applied
in each third of the duration of the bursts. Thus, we obtained one curve of the
averaged pulse shape for each different section of the bursts (as shown in
Fig. 1). The average profile is notably identical in each 1/3 of T90 (we
estimate the differential spread, S, to be
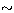 1%).
1%).
We have shown the lack of temporal evolution of the peak width in the context of an
average of many bursts. Now, we expand our analysis to individual bursts. An excellent
analysis has been provided by
[Norris et al. (1995)],
where they examined the temporal profiles of bright GRBs by fitting those profiles with
pulses. From the set of bursts that they analysed, we used the 28 bursts with the
characteristic of having seven or more fitted pulses within their duration. To obtain
the temporal dependency of the pulse width, we selected the five largest peaks in each
burst and fit their FWHM to a function of the arrival time, 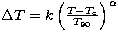 . We chose this model because
the expected dependency from the "external'' shock model scales as
. We chose this model because
the expected dependency from the "external'' shock model scales as
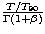 (if a relativistic shell is responsible for the shape in the time
histories, T0 should be proportional to T90; see
[Fenimore et al. 1996]).
The purpose
of the
(if a relativistic shell is responsible for the shape in the time
histories, T0 should be proportional to T90; see
[Fenimore et al. 1996]).
The purpose
of the 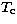 parameter is to correct the BATSE time to the time since the
beginning of the explosion. Figure 2 shows the distribution of the power law
indexes (
parameter is to correct the BATSE time to the time since the
beginning of the explosion. Figure 2 shows the distribution of the power law
indexes (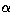 ) for the set of bursts analysed. The distribution shows that in
individual bursts the pulse width does not increase throughout their duration as
predicted by the external shock model, for which
) for the set of bursts analysed. The distribution shows that in
individual bursts the pulse width does not increase throughout their duration as
predicted by the external shock model, for which 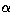 is expected to be 1 (or
larger if deceleration is occurring). In fact, most bursts show a diminution in pulse
width.
is expected to be 1 (or
larger if deceleration is occurring). In fact, most bursts show a diminution in pulse
width.
![\begin{figure}
\includegraphics [width=8.8cm]{rome98_fig2.eps}\end{figure}](/articles/aas/full/1999/15/r23/Timg18.gif) |
Figure 2:
Distribution of the 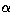 parameter from 28 bright BATSE bursts with
durations longer than 1.5 s. The pulse width ( parameter from 28 bright BATSE bursts with
durations longer than 1.5 s. The pulse width (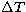 ), as expected for the external
model, should scale as T/T90. We fit ), as expected for the external
model, should scale as T/T90. We fit 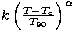 to find the temporal evolution of the pulse width in each
burst. The dashed line is the expected index value, to find the temporal evolution of the pulse width in each
burst. The dashed line is the expected index value, 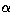 , for a single relativistic
shell ( , for a single relativistic
shell (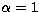 ). The distribution shows that the vast majority of the bursts present
no time evolution (or negative) of the pulse width ). The distribution shows that the vast majority of the bursts present
no time evolution (or negative) of the pulse width |


Up: Temporal evolution of the
Copyright The European Southern Observatory (ESO)
![]() . We chose this model because
the expected dependency from the "external'' shock model scales as
. We chose this model because
the expected dependency from the "external'' shock model scales as
![]() (if a relativistic shell is responsible for the shape in the time
histories, T0 should be proportional to T90; see
[Fenimore et al. 1996]).
The purpose
of the
(if a relativistic shell is responsible for the shape in the time
histories, T0 should be proportional to T90; see
[Fenimore et al. 1996]).
The purpose
of the ![]() parameter is to correct the BATSE time to the time since the
beginning of the explosion. Figure 2 shows the distribution of the power law
indexes (
parameter is to correct the BATSE time to the time since the
beginning of the explosion. Figure 2 shows the distribution of the power law
indexes (![]() ) for the set of bursts analysed. The distribution shows that in
individual bursts the pulse width does not increase throughout their duration as
predicted by the external shock model, for which
) for the set of bursts analysed. The distribution shows that in
individual bursts the pulse width does not increase throughout their duration as
predicted by the external shock model, for which ![]() is expected to be 1 (or
larger if deceleration is occurring). In fact, most bursts show a diminution in pulse
width.
is expected to be 1 (or
larger if deceleration is occurring). In fact, most bursts show a diminution in pulse
width.