

Up: Monochromatic morphologies of Abell nebulae
Subsections
The fact that these images are absolutely calibrated allows physical properties
to be derived from these observations. The total nebular fluxes in H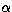 ,
[N II], and [O III] are obtained by integrating over the nebular
image for each of these filters. The corresponding logarithmic extinction
values listed in Table 2 are taken from Cahn et al. 1992).
,
[N II], and [O III] are obtained by integrating over the nebular
image for each of these filters. The corresponding logarithmic extinction
values listed in Table 2 are taken from Cahn et al. 1992).
The total flux  emitted by the H
emitted by the H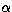 line from a
uniform density sphere of radius R is given by
line from a
uniform density sphere of radius R is given by
|  |
(3) |
where  is the line emission coefficient, and D is the distance to the
nebula. For a recombination line,
is the line emission coefficient, and D is the distance to the
nebula. For a recombination line,  is often expressed in terms
of the effective recombination coefficient
is often expressed in terms
of the effective recombination coefficient
|  |
(4) |
where  and
and  are the electron and proton densities respectively.
The flux in the recombination line can then be written as
are the electron and proton densities respectively.
The flux in the recombination line can then be written as
|  |
(5) |
In practice, a filling factor  is often used to take into account
the actually observed nebular structures which are far from homogeneous (see
morphologies displayed in a recent report by Hua et al. 1998). Its value
lies between 0.3 and 0.7. The ionized mass of the nebula is then given by
is often used to take into account
the actually observed nebular structures which are far from homogeneous (see
morphologies displayed in a recent report by Hua et al. 1998). Its value
lies between 0.3 and 0.7. The ionized mass of the nebula is then given by
|  |
(6) |
where  is the mean atomic mass per H atom. Combining Eqs. (5)
and (6), the ionized nebular mass can be expressed in terms of
the angular radius (
is the mean atomic mass per H atom. Combining Eqs. (5)
and (6), the ionized nebular mass can be expressed in terms of
the angular radius (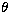 ) and H
) and H flux as
flux as
|  |
(7) |
where  . Since both
. Since both 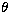 and
and  (i.e. our measured
(i.e. our measured  fluxes corrected for extinction using
radio - or optical when radio data are missing -
fluxes corrected for extinction using
radio - or optical when radio data are missing -  values quoted
in Table 2) are measured in our images, the ionized masses for the nebulae can
be obtained as a function of their distances.
The effective recombination
coefficients for the recombination lines of H are tabulated in Hummer & Storey
(1987). For example,
values quoted
in Table 2) are measured in our images, the ionized masses for the nebulae can
be obtained as a function of their distances.
The effective recombination
coefficients for the recombination lines of H are tabulated in Hummer & Storey
(1987). For example,  at
at 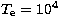 K
and
K
and  cm-3 has a value of 8.65 10-14 cm3 s-1, and
Eq. (7) can be written as
cm-3 has a value of 8.65 10-14 cm3 s-1, and
Eq. (7) can be written as
|  |
(8) |
with 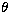 in arcmin, D in kpc, and
in arcmin, D in kpc, and  in 10-12 erg cm-2 s-1 units.
The derived values of Mi (assuming
in 10-12 erg cm-2 s-1 units.
The derived values of Mi (assuming  ) are given in Table 2. We
adopted the major axis values for elongated PNe (A 13, A 36). Given the
uncertainties in the distances, the derived ionized masses (mainly less than 1
) are given in Table 2. We
adopted the major axis values for elongated PNe (A 13, A 36). Given the
uncertainties in the distances, the derived ionized masses (mainly less than 1
 ) for the other Abell PNe are not drastically different from most
evolved PNe.
) for the other Abell PNe are not drastically different from most
evolved PNe.


Up: Monochromatic morphologies of Abell nebulae
Copyright The European Southern Observatory (ESO)
![]() ,
[N II], and [O III] are obtained by integrating over the nebular
image for each of these filters. The corresponding logarithmic extinction
values listed in Table 2 are taken from Cahn et al. 1992).
,
[N II], and [O III] are obtained by integrating over the nebular
image for each of these filters. The corresponding logarithmic extinction
values listed in Table 2 are taken from Cahn et al. 1992).
![]() emitted by the H
emitted by the H![]() line from a
uniform density sphere of radius R is given by
line from a
uniform density sphere of radius R is given by




