![\begin{displaymath}
I_k
=
\sum_{j=1}^n A_j [ 1 + M_1\cos(p_k+f_xx_j+f_yy_j)
\\ \quad+
M_2\cos 2(p_k+f_xx_j+f_yy_j) ].\end{displaymath}](/articles/aas/full/1999/14/ds1699/img141.gif)
For a given transit the expected signal is modeled as the sum of the signals
from the individual components, using Eqs. (4) and (5).
Thus,
![\begin{displaymath}
I_k
=
\sum_{j=1}^n A_j [ 1 + M_1\cos(p_k+f_xx_j+f_yy_j)
\\ \quad+
M_2\cos 2(p_k+f_xx_j+f_yy_j) ].\end{displaymath}](/articles/aas/full/1999/14/ds1699/img141.gif) |
(13) |
 |
 |
 |
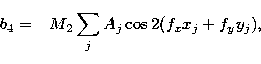 |
 |
(14) |
The trigonometric functions in Eq. (14) mean that the signal
parameters bi depend in a highly non-linear manner on the model parameters
which affect xj and yj. For instance, in terms of a displacement of
one of the point sources, the effect on b4 and b5 is approximately
linear only for displacements less than about ![]() arcsec,
corresponding to 1 rad change in the modulation phase. In the aperture
synthesis imaging this non-linearity is manifest in the complex structure
of the "dirty beam" (Fig. 4) at all spatial scales larger
than about 0.1 arcsec. Additional non-linearities in the complete object
model may result from the geometrical description of the source positions,
e.g. in terms of orbital elements.
arcsec,
corresponding to 1 rad change in the modulation phase. In the aperture
synthesis imaging this non-linearity is manifest in the complex structure
of the "dirty beam" (Fig. 4) at all spatial scales larger
than about 0.1 arcsec. Additional non-linearities in the complete object
model may result from the geometrical description of the source positions,
e.g. in terms of orbital elements.
The non-linearity of the object model has two important consequences for the model fitting. Firstly, it is usually necessary to use a non-linear, iterative adjustment algorithm, such as the Levenberg-Marquardt method (Press et al. 1992). Secondly, a good initial guess of the model parameters is usually required. In particular the parameters directly affecting the positions of the point sources need to be specified to within (what corresponds to) a few tenths of an arcsec. Without a good initial guess, the adjustment algorithm is likely to converge on some local minimum, typically resulting in positional errors of (approximately) an integer number of grid periods. The correct solution, corresponding to the global minimum, may in principle always be found through sufficiently extensive searching of the parameter space. Alternatively, sufficiently good initial guesses of the point source positions can often be obtained from the aperture synthesis imaging.
Various least-squares model fitting procedures were used for the reduction of double and multiple stars during the construction of the Hipparcos Catalogue (see Mignard et al. 1995 and references therein). The double-star processing of the NDAC data reduction consortium (Söderhjelm et al. 1992) essentially used the technique outlined above, taking the so-called Case History Files (a precursor to the TD) as input.
Perhaps the greatest potential of the TD lies in the possibility to combine the Hipparcos data with independent observations from other instruments and epochs. For instance, full determination of a binary orbit generally requires data covering at least a whole period. Ground-based speckle observations can sometimes provide this, constraining the geometry of the relative orbit much better than the Hipparcos data alone, and in turn leading to a better-determined space parallax. In some favourable cases the location of the mass centre in the relative orbit (and hence the mass ratio) can be determined (Söderhjelm et al. 1997; Söderhjelm 1999).
One complication of the Hipparcos double star processing has been the wide variety of applicable object models, and the consequent need to experiment and interact with the solutions. This process may be much facilitated by using general and flexible software for the model fitting, rather than highly specialized routines. An example of this is given below.
GaussFit (Jefferys et al. 1988a, 1988b) is a general program for the solution of least squares and robust estimation problems, developed as a platform to facilitate astrometric reduction of data from the Hubble Space Telescope. It is written in the C programming language and may thus be run under a variety of operating systems. In this section we outline the use of GaussFit for model fitting to the TD, again using the binary HIP 97237 as illustration.
GaussFit was used by Söderhjelm (1999) in a systematic re-examination of the solutions for several double and multiple objects, through a combination of TD with ground-based observations. Although not illustrated in the example below, the introduction of additional data (e.g. relative positions from speckle observations) is quite straightforward by means of GaussFit.
To run GaussFit, the user must supply several input files. During execution these files are read (and sometimes modified) by GaussFit, and additional output files generated. For application to the TD model fitting the following input files are required.
![\begin{figure}
\includegraphics [width=10cm,clip]{ds1699f9.eps}\end{figure}](/articles/aas/full/1999/14/ds1699/Timg151.gif) |
Figure 9: Part of the GaussFit output (slightly edited) obtained while fitting the double star model in Fig. 8 to the TD for HIP 97237 |
Figure 8 is an example of a GaussFit model file.
It describes a binary with a fixed positional offset between the
components (i.e. a long-period binary). The model parameters
are thus the astrometric parameters of the primary relative to
the reference point (![]() ,
,
![]() ,
, ![]() ,
,![]() ,
, ![]() ),
the position of the secondary relative to the reference point
(
),
the position of the secondary relative to the reference point
(![]() ,
,
![]() ); and the intensities of the
components,
); and the intensities of the
components, ![]() ,
, ![]() .The components are assumed to have the same parallax and proper
motion. The expressions within the
.The components are assumed to have the same parallax and proper
motion. The expressions within the ![]() functions
are easily recognized as the equations of condition,
Eq. (14), written in terms of the model parameters.
The five
functions
are easily recognized as the equations of condition,
Eq. (14), written in terms of the model parameters.
The five ![]() statements are divided among two
statements are divided among two
![]() loops (which means that the data file is forced
to be read twice in each iteration): the reason is that GaussFit
in its standard distribution version cannot handle more than
four simultaneous equations of condition.
loops (which means that the data file is forced
to be read twice in each iteration): the reason is that GaussFit
in its standard distribution version cannot handle more than
four simultaneous equations of condition.
The model in Fig. 8 was applied to the TD of
HIP 97237, using as starting approximation
(3600, 3600, 0, 0, 0, 0.04, 4000, 4300, 0.02) for the variables
in the parameter list (cf. Sect. 4.3). The "fair''
metric with an asymptotic relative efficiency of 0.95 was
used for robust estimation of the parameters
(Jefferys et al. 1988a). Part of the output file, containing
the results of the final (10th) iteration, is shown in
Fig. 9. It should be noted that the estimated
standard errors (sigma values) given in the output file have
already been scaled by ![]() , using the chi-square
(
, using the chi-square
(![]() ) and degrees of freedom (
) and degrees of freedom (![]() ) given at the end of the
file. Adding the results of the model fitting to the reference
point data (Sect. 4.3) and using the magnitude
conversion formula
) given at the end of the
file. Adding the results of the model fitting to the reference
point data (Sect. 4.3) and using the magnitude
conversion formula ![]() we obtain the following
estimated parameters of the binary HIP 97237 (ICRS, epoch J1991.25):
0pt
we obtain the following
estimated parameters of the binary HIP 97237 (ICRS, epoch J1991.25):
0pt
Copyright The European Southern Observatory (ESO)