3 Observations and data reduction

3.1 Observations

The observations were made at the Southern European Southern Observatory (La Silla, Chile) by Doublier and Caulet using the 1.54 m Danish Telescope, during two periods: April 29 - May 3 and December 20-23, 1995. In April-May, the direct camera was equipped with a thinned back-illuminated 1024 $\times$ 1024 pixel Tektronix CCD (ESO #28) with a pixel scale of 0.36''. In December, DFOSC (Danish Faint Object Spectrograph and Camera) was equipped with the thinned Loral 2048 $\times$ 2048 CCD#17 with a pixel scale of 0.38''.

Each galaxy field was exposed three times with a dithering step equal to at least the size of the galaxy in order to correct for blemishes on the CCD chip. Short exposures were taken to avoid saturation of bright stars in the fields that could create ghosts and uneven background, CCD saturation and bleeding. The data were bias subtracted, flat fielded and combined in the standard way, using the IRAF package.

During both runs, the weather was clear, and the seeing was between 0.9 and 1.1'' (FWHM measured on field stars close to the objects). Weather conditions did not vary much during the nights, the variations of airmass-dependent terms in Eqs. (1) and (2) were less than 0.005. In addition, we observed the galaxies close to meridian, to reduce the variation of atmospheric absorption. Therefore, seeing and/or absorption were not important effects when we combined the frames, even those taken during different nights.

We used Johnson B and R ESO filters in combination with the CCDs, producing instrumental systems that are easy to convert to the standard Cousins system. The color terms were found to be negligible for both filters. For the photometric calibration, some [Landolt(1992)] equatorial standard stars were followed throughout the nights at different airmasses. Table 2 summarizes the observation log, as well as the signal-to-noise ratio obtained at the surface brightness of 25 mag/arcsec² in both bands.

**Table 2:** Observing log
$\begin{tabular} {l c c r@{~\&~}l} \hline \multicolumn{1}{l}{object Name}& \multi... ...(25): Signal to noise ratio at $\mu$\space = 25 mag/arcsec$^2$.}\\ \end{tabular}$

3.2 Standard stars

Aperture photometry was performed on standard Landolt stars. We obtained the following equations which are used to convert our instrumental magnitudes (b, r) and colors to the Johnson-Cousins system, the values in parenthesis correspond to those obtained during the December run:

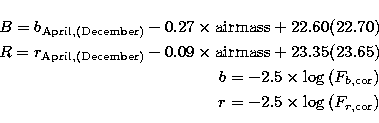$\begin{eqnarray} B = b_{\rm April, (December)} - 0.27 \times {\rm airmass} + 22.... ...{(F_{ b,\rm cor} )} \\ r = -2.5 \times \log {(F_{ r,\rm cor} )} \end{eqnarray}$ (1)

(2)

(3)

(4)

where $F_{ b,\rm cor}$ and $F_{ r,\rm cor}$ are the sky subtracted fluxes in counts per second, in B and R bands respectively.

The atmospheric absorption coefficients and zero points magnitudes were determined each night in a standard way. The values given in the above equations are average values for each observing period.

The Johnson R filter includes the H $_\alpha$ emission line in the rest frame; all objects have low redshift, and their H $_\alpha$ emission is always included in the measured R flux. Over the galaxy, the H $_\alpha$ flux is less important than a substantial background from an evolved stellar population, but it may, in some cases, produce a local red excess inside the galaxies, especially in star forming complexes that may have a large equivalent width of H $_\alpha$ emission.

3.3 Galaxy photometry

3.3.1 Data reduction

The surface photometry of the galaxies was done with our own MIDAS (see Paper I) macro-procedures, and the reader is referred to Paper I for a complete description of the methods used. We briefly summarize the method: an isophotal integration of the flux was done without setting any constrain on the geometry of the isophotes (equivalent profile method, [De Vaucouleurs1959]; [Fraser1977]). After a careful estimation of the local sky background, the following photometric parameters were derived (using the notation from [De Vaucouleurs1959]): the equivalent radius $r_{\rm eff}$ and r_0.25, within which are contained half and a quarter of the total luminosity respectively; they were derived from the curve of growth of the instrumental magnitudes, before Galactic foreground extinction correction. The asymptotic magnitude was extrapolated from the last 4 points on the integrated magnitude curve of growth. The surface brightnesses at $r = r_{\rm eff}$ and r_0.25, and the average surface brightness inside the effective radius, $<\mu_{\rm eff}\gt$ , were also measured. We have checked that the variation of the derived parameters with different values of extinction is not large, considering the errors on the measurement of the radius, and the estimation of the asymptotic magnitude. For instance, adding an arbitrary value of A_B = 0.3 mag to the galaxy leads to decrease the effective radius by 0.2 arcsec. This is not significant considering the average seeing of 1.1'' we had throughout our runs.

The sky background was checked to be flat in the vicinity of the objects. Since our procedures to derive the surface photometry take into account the local sky background, we wanted to avoid sky background subtraction on the image. In the cases of sky gradients under the objects, we subtracted a two-dimensional fit of the sky from the images.

As in Paper I, to increase the signal-to-noise ratio of the faint outermost isophotes, we have performed the isophotal integration in two steps. First, we used the direct image to produce a surface brightness profile, valid at bright intensity levels, then we smoothed the images with a Gaussian filter of a few pixels of width that matched the seeing disk of the images, and we built a second profile. Finally, the two surface brightness profiles were merged.

3.3.2 Errors

The errors in magnitudes and surface brightness were estimated assuming Poisson statistics, and taking into account the errors on the sky background estimation (based on local 1- $\sigma$ variation). We used the relation given by [Saglia et al.(1997)].

The errors on the asymptotic magnitudes are more difficult to estimate accurately because pure Poisson statistics do not apply, and due to the extrapolation of a magnitude based on the last four points of the photometric profile. We estimate that the errors are of the order of those made on the photometric calibration, e.g. 1%.

$\begin{figure} \includegraphics [clip]{figure1a.ps} \end{figure}$

Figure 1: a) Atlas of isophotal maps and surface brightness profile distributions. This atlas presents the isophotal B maps and surface brightness distribution in the B and R bands. On the top right corner, the B-R color distribution is shown. The scale bar at the bottom of the map represents 1 kpc. The threshold brightness is indicated, the isophotal step on the map is 0.5 magnitude. Orientation is North up East left for the galaxies taken in December 1995, and North down and East right for the images taken in April-May 1995

$\begin{figure} \includegraphics [clip]{figure1b.ps} \end{figure}$

Figure 1: b) continued

$\begin{figure} \includegraphics [clip]{figure1c.ps} \end{figure}$

Figure 1: c) continued

$\begin{figure} \includegraphics [clip]{figure1d.ps} \end{figure}$

Figure 1: d) continued

$\begin{figure} \includegraphics [clip]{figure1e.ps} \end{figure}$

Figure 1: e) continued

$\begin{figure} \includegraphics [clip]{figure1f.ps} \end{figure}$

Figure 1: f) continued

$\begin{figure} \includegraphics [clip]{figure1g.ps} \end{figure}$

Figure 1: g) continued

$\begin{figure} \includegraphics [clip]{figure1h.ps} \end{figure}$

Figure 1: h) continued

$\begin{figure} \includegraphics [clip]{figure1i.ps} \end{figure}$

Figure 1: i) continued

$\begin{figure} \includegraphics [clip]{figure1j.ps} \end{figure}$

Figure 1: j) continued

$\begin{figure} \includegraphics [clip]{figure1k.ps} \end{figure}$

Figure 1: k) continued

$\begin{figure} \includegraphics [clip]{figure1l.ps} \end{figure}$

Figure 1: l) continued

**Table 3:** Results of the photometry
$\begin{tabular} {l ccccccc} \hline \multicolumn{8}{l}{}\\ [-3mm] \multicolumn{1}... ...ce colors, defined as the $r_{\rm eff} / r_{0.25}$\space ratio.}\\ \end{tabular}$

3.3.3 Photometric results

The results of the photometry are presented in Fig. 1 and Table 3. For each galaxy, Fig. 1 shows the isophotal map in B, the surface brightness distribution in the B and R bands, and the B-R distribution. The orientations are from Haro 14 to Tol 3 North to the top and East to the left, and from Fairall 6 to Tol 1937-423 North down and East right. Table 3 collects the observable parameters derived from the photometry.

The data in Table 3 have not been corrected for Galactic foreground extinction. Extinction has been applied when deriving the integrated parameters such as the absolute magnitudes in B and R (M_B and M_R resp.). We used the E(B-V) maps of [Burstein & Heiles1982] and derived the absorption coefficients using Savage & Mathis (1979) relations: A_B = 4.0 E(B-V) and A_R = 2.52 E(B-V).

3.4 B-R color profiles

The method used to trace the B-R color profiles is the same as in Paper I. We interpolated the surface brightness (SB) profiles in B and R because the sampling of the profiles are different in each band, and subtracted the resulting profiles from one another. The results are in excellent agreement with those obtained directly by performing the photometry on B-R two-dimensional maps of several galaxies (Mk 996, Haro 14 and Fairall 301), only of better signal-to-noise toward the faint regions. Since we did not correct neither the profiles, nor the images from the seeing effects, the profiles are not to be seriously considered within the central first 1'' radius.

The errors are calculated assuming that the errors in B and R are independent, using:

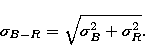$\begin{eqnarray} \sigma_{B-R} = \sqrt{\sigma_{B}^2 + \sigma_{R}^2}.\end{eqnarray}$ (5)

Here, we should emphasize that, in the central part of the BCDGs, the B-R colors could be contaminated by nebular emission such as H $_\alpha$ present in the R band filter. The equivalent width of this line reaches generaly a few hundreds of Angström, therefore it can contribute significantly within the R filter to the total R emission. The outer parts of the BCDGs, however, do not suffer from such contamination, since the emission can be supposedly attributed to the stellar component only.

3.5 Comments on individual objects

Most of our objects show several star forming regions or knots with B-R colors different from those of their host galaxies. We note that the knots get bluer away from the photometric center of the galaxy. This behaviour could reflect a variation of internal reddening due to dust, or more likely an age spread. However, those objects do not show obvious presence of dust as the ratio between the recombination lines of hydrogen H $\alpha$ /H $\beta$ remains close to a value of 3. Some galaxies have a single compact star forming knot ( $\le$ 5-10''), whereas , in other galaxies, "multi-knots'' regions are distributed over more than 2/3 of the galaxy's surface.

As in Paper I, the morphology of several BCDGs in the present sample departs conspicuously from axisymmetric shapes, for instance Tol 1937-423, UM 461, in the present sample. Because irregular morphology in star forming galaxies can be explained by mergers and dynamical interaction, and because our galaxies are not associated with known companions (except UM 465), we have searched for faint galaxy companions close to our BCDGs on our deep optical images. The results are presented in Sect. 4.3. We discuss now in detail the properties of individual galaxies. Other distortions (boxy isophotes, isophote apparent major axis rotation) are noted in the inner regions of several galaxies.

A summary of the anomalies noted in the BCDGs studied in our sample is given in Table 4 at the end of this section.

Haro 14 (NGC 244, VV728; North up, East left): this galaxy has several blue knots (0.5 $\le$ B-R $\le$ 0.8) embedded in a bright amorphous central region out of which several curved chain-like features are protruding. These "chains'' have a knotty structure and are perhaps chains of star clusters and their associated H II regions. The bright amorphous central region is off-centered with respect to the outermost isophotes of the galaxy. A redder, bright knot (B = 18.19, B-R = 1.2) seems to be a "nucleus'' or a site of stellar formation more evolved than the bluest knots. These features are surrounded by a red, almost circular envelope containing also low brightness knotty structures. The surface brightness distribution in B and R shows two "plateau'' components (less suggestive in B) at r = 3.5'' and 22'', with a strong rise in luminosity towards the center due to the presence of the "nucleus''. The overall shape remains close to an exponential distribution, implying that Haro 14 could be a disk-dominated object with a large amount of Population I objects. Those results are in very good agreement with those of Marlowe et al. (1997), at least up to $r_{\rm e}$ = 25 arcsec, which is their limiting radius.

The integrated color of the galaxy is not very blue: B-R = 1.1, suggesting the presence of an evolved underlying stellar population, also indicated by the off-centered circular envelope.

$\begin{figure} \includegraphics [width=8.2cm,clip]{figure2a.ps} \includegraphic... ...e2b.ps} \includegraphics [angle=-90,width=8.5cm,clip]{figure2c.ps} \end{figure}$

Figure 2: a) B surface brightness distributions of the Elliptical-like BCDGs. The figure shows the B surface brightness distribution of the 13 objects whose SB distribution is clearly dominated by a r^1/4 law, as a function of the reduced variable: ( $r/r_{\rm e}$ )^1/4, from the De Vaucouleurs law. The dashed line represents the slope of de Vaucouleurs law (8.327). a) Mk 996, b) Mk 600, c) Tol0513-393, d) Tol 0645-376, e) Tol 0957-279, f) Tol 1004-296, g) II SZ 34, h) 13209-2723, i) Tol 1434+032, j) Tol 1924-416, k) Fairall 6, l) Tol 1937-423 b) Profile decomposition of Mk 996: The figure shows the decomposition of the surface brightness profile of Mk 996 in the B band: the bold dashed line represents the exponential component, while the faint dashed line represents both the r^1/4 and exponential components. Note the presence of the compact exponential component in the central regions, it may be the exponential seen by [Thuan et al.(1996)] on their HST images. c) Profile decomposition of Tol 1434+032: the bold dashed line represents the exponential component, while the faint dashed line represents both the r^1/4 and exponential components. Note that the fit gives an excess of light in the central parts of the galaxy. It is probable that this galaxy possesses a core component much older that the star forming regions, as indicated by its red color

**Table 4:** Morphological anomalies of the sample
$\begin{tabular} {c c c c c } \hline \multicolumn{1}{c}{}& \multicolumn{1}{c}{}& ... ...UM 461 & & Tol 1448& \\ & Tol 1924 & & Tol 1937 & \\ \hline\hline\end{tabular}$

Mk 996 (North up, East left): Previous observations of this galaxy made under poor atmospheric conditions, have been reported in Paper I. The new data establish the elliptical-like character of this object. This BCDG has a regular structure with slightly distorted isophotes near the center, due to the presence of a dust lane. The surface brightness distribution is largely dominated by a r^1/4 law, with one noted deviation: an excess of light between 5'' and 15'' (surface brightness of 22 mag arcsec^-2 and 25 mag arcsec^-2 repectively, see Fig. 2b). These present observations resolve the inconsistency between our results from Paper I and the high spatial resolution HST observations (WF-camera) of [Thuan et al.(1996)]. They have performed surface photometry of this galaxy, and fitted their observations with an exponential up to a radius of 20'', and reported the presence of an excess of light at larger radii. Indeed, our data which are deeper and show a larger part of the galaxy, definitely show this excess. The surface brightness distribution is better fitted by a r^1/4 law with a small compact exponential component in the central regions.
UM 417 (North up, East left): this cometary-like faint BCDG has a bright compact star forming region at the South-East end. The light distribution is well fitted by neither a pure exponential nor a r^1/4 law. The profile shape is very similar to that of SBS 1331+493, a galaxy from our Northern Sample (Paper I). The color distribution wriggles near the center with a zero colour gradient, the center being bluer.
Mk 600 (North up, East left): [Kinman & Davidson1981, Kinman & Davidson (1981)] give a photographic B magnitude inside the Holmberg diameter of 15.42, in excellent agreement with our measurement, B = 15.47.
This galaxy has a blue core (B-R $\sim$ 0.5) embedded in a diffuse bright area elongated along the major axis. Another small star forming region (B-R $\sim$ 0.4) is conspicuous at 13'' South-east of the center. The outer/low surface brightness envelope has a boxy shape with a redder color B-R $\sim$ 1.5 with a strong center-to-edge color gradient. Two small angular diameter objects are located to the South-East of the isophotes of Mk 600. The closest has a diameter of 13'', and is elongated along the major axis of the main galaxy with a North-West extension. The second object is also resolved (FWHM of 2.5''), located further away along the major axis. Without spectroscopic redshift, the nature of these objects is uncertain. Nevertheless, their magnitudes 18.90 and 20.50 (B and R respectively), and their colors $B-R\sim$ 0.6 and 1.1, suggest the possibility that they are faint galaxy companions near Mk 600. At the North-West boundary of Mk 600, a low surface brightness blue extension is also detected. The surface brightness distribution of Mk 600 is consistent with a dominant r^1/4 law, but some deviations are obvious.
Fairall 301 (NGC 1522; North up, East left): the RC3 catalog ([De Vaucouleurs et al.1991]) quotes a total B magnitude of 13.93 $\pm$ 0.13 from [Bergvall & Olofsson1986], comparable to our measured B of 14.15 mag.
This BCDG is embedded in a faint envelope; it has regular isophotes, a bright blue core (B-R $\sim$ 0.5), with two separated knots slightly off-centered. The brightness gradient towards the outer regions is more pronounced on one side (North-East) than the other. The major axis of the central star-forming region does not coincide with that of the whole galaxy. The SB distribution beyond a radius of 10'' is dominated by an exponential law.
Tololo 0513-393 (North up, East left): this is a very compact blue galaxy, barely a dwarf with M_B = -17.66, showing faint North-South extensions. The nucleus is off-centered with respect to the outer isophotes. The surface brightness distribution is consistent with a dominating bulge-like structure and a faint underlying exponential component. The morphology is difficult to ascertain because of the small angular size (r₂₆ $\sim$ 4'') due to the large distance of this galaxy, the most distant in our sample with a recession velocity of 14370 km s^-1. The color distribution shows no large color gradient; but the outer parts are redder than the central parts. There is some evidence for blueing at $r_{\rm e}$ = 3'' in our data, and Terlevich et al. (1991) report a Balmer decrement of 3.45 in the central star forming region. Thus, the red color of the nucleus is most probably due to dust extinction inside the starforming region, rather than caused by an evolved star population.
Tololo 0610-387 (North up, East left): this slightly distorted galaxy shows a small blue South-West extension (B-R $\sim$ 0.8). The isophotes appear to be rotating, although the presence of foreground galactic stars may alter the shape of the outer isophotes. The surface brightness distribution is slightly different in B and R. It is well fitted by an exponential in the B band, but in the R band, a two component profile is required: an exponential that follows the B surface brightness distribution, and a shallower redder envelope. This galaxy is red in our sample (B-R = 1.76); it has a strong gradient in B-R, the center being much bluer: B-R $\sim$ 0.9.
Tololo 0645-376 (North up, East left): This intrinsically luminous object (M_b = -17.97) is not a dwarf galaxy by our selection criteria (absolute magnitude fainter than -16.5). it is blue (B-R = 0.97), large (r₂₆(B) $\sim$ 5 kpc), and elongated along the East-West direction. It displays a central star forming region distributed along the major axis, with a bright stellar-like nucleus (FWHM = 1.6''). The outer envelope shows two weak extensions, reminiscent of warps present in the outer parts of some edge-on disk galaxies, but these features, also visible on the B-R map could be tidal remnants from a past interaction. The B-R map shows a local maximum West of the center, extending North-West, that suggests the presence of a dust lane obscuring partly the star forming region. The Balmer decrement value, H $\alpha$ /H $\beta$ $\sim$ 4.3, observed by Terlevich et al. (1991) supports the hypothesis of some dust content. On the isophotal map, the extension visible South-East from the center is caused by a superimposed faint blue Galactic star. The surface brightness distribution is consistent with a dominant r^1/4 law with a moderate color gradient.
Tololo 0954-293 (North up, East left): the only available other photometric measurement is from Bohuski et al. (1978), who gives B = 16.61 inside an aperture of 11.6'', which compares to our measurement of B = 16.49.
The recession velocity of this galaxy is 2055 km s^-1; it was kindly supplied to us by G. Dudziak (private communication), inferring M_B = -16.26. The morphological structure of this galaxy is reminiscent of the Magellanic type galaxy NGC 4449, or II ZW 33 ([Loose & Thuan1986b]). A very blue (B-R $\sim$ 0.4), extended, bar-shaped star forming region out of which protrude two opposite clumpy extensions, is embedded in a boxy envelope. The surface brightness profile is composite: the inner regions can be fitted by an exponential law with a steep central braightness gradient; and a very shallow outer envelope can be fitted by another exponential law with a faint central brightness.
Tololo 0957-279 (Tololo 2; North up, East left): the galaxy has an amorphous overall shape; it is elongated along an East-West direction. The bright central region shows a complex pattern, with a curved chain of luminous blue knots (B-R $\sim$ 0.3). The brightest knot near the center is elongated like the "mini-bar'' seen in numerous hot-spot galaxies (dwarf HII hotspot galaxies, [Salzer et al.1989b]) The B-R color contours suggest the presence of a dust lane across the star forming region. A large, red and shallow extension around the bright central region is visible along the major axis. The B and R band surface brightness distributions are both consistent with a dominant r^1/4 law with some local deviations. In addition, the envelope beyond r = 25'' indicates the presence of an underlying exponential component. This is in agreement with Kunth et al. (1988) observation that the disk component accounts for only one third of the luminosity of Tololo 2. We also note a strong color gradient in the outer regions, where the outermost parts of the envelope become very red.
Tololo 1004-296 (Tololo 3, NGC 3125; North up, East left): for this BCDG, we obtain a total B magnitude of 14.2 which is 0.7 magnitude fainter than Bergvall & Olofsson (1986) value, quoted in RC3, and 0.1 brighter than Kunth et al. (1988)'s value. The presence of 3 superimposed Galactic stars falling within the aperture used by Bergvall & Olofsson could explain the measurement discrepancies.
The overall shape is roughly elliptical with an elongated bright central region of asymmetric brightness distribution. An elongated bright knot pointing North-East of the central "nucleus'' leads to a morphology similar to that of Fairall 301. The bluest knot in the star forming region has a B-R color of 1.1, suggesting the presence of an evolved stellar population. The surface brightness distribution is consistent with a dominant r^1/4 law, in agreement with another photometric observation of this galaxy ([Kunth et al.1988]).
Tololo 1108+098 (Fairall 6; North is down, East right): This object shows a kidney-like bright central region with a compact blue (B-R $\sim$ 0.2) nucleus (FWHM = 2''). Several connected knots are grouped along a curve extending East-West from the center. These features are star-forming sites, as evidenced by their blue colors (B-R $\sim$ 0.4). The outer envelope is elliptical with a boxy shape. The surface brightness distribution is fairly consistent with a dominant r^1/4 law, although there is a break in the light profile at about 4'' from the center coincident with the two secondary star forming regions.
UM 465A and B (Mk 1308, IC 745; North down, East right): Data for this pair of galaxies previously observed by us at the Pic du Midi Observatory, were published in Paper I. The present La Silla data have a better S/N ratio. It allows us to derive the surface photometry of the companion, UM 465B which is separated from the main galaxy, UM 465A, by 38'' (2 kpc projected distance). The main galaxy has regular external isophotes; they become asymmetric towards the center, and there is a steep surface brightness gradient opposite to the companion direction. The color maps show that the star formation event occurs in the center and produces a small extension in the North-East direction. High spatial resolution HST images (WFPC2, archive images) show clearly the extension due to a chain of star forming knots extending south. A dust lane is also clearly visible north of the center.
The companion exhibits a high surface brightness knot and a tail extending opposite to the direction of the main galaxy. The bright compact knot of the companion is very red (B-R $\sim$ 1.8) and may be the obscured nucleus. The star forming region extends across the whole companion ( $0.5\le B-R \le 0.9$ ), a possible consequence of the gravitational interaction between the two galaxies.
Both galaxies have dominant exponential surface brightness profiles with very steep surface brightness gradients in B and R, but departures from the pure exponential law are obvious.
Salzer et al. (1989b) give a total B magnitude of 14.14, and a B-R color of 1.24 for UM 465A, in fair agreement with our values.
UM 461 (North down, East right): This small galaxy with a double nucleus exhibits an external envelope distorted strongly towards the South-West, suggesting a recent tidal event. This is strongly supported by the fact that UM 461 belongs to a small group of dwarf galaxies including UM 462. However, the recent HI observations done by Van Zee et al. (1998) tend to show that no tidal interaction takes place.
The two "nuclei'' do not have the same color: the brighter (B = 17.41) is bluer (B-R $\sim$ 0.5) compared to the other with B = 18.62 and B-R $\sim$ 1.1. The surface brightness distribution is composite and is fitted by the sum of two exponential laws. The outer envelope (beyond B = 26.75 mag/arcsec² and R = 26 mag/arcsec²) has a very shallow brightness gradient. Moreover, the HI maps obtained by Van Zee et al. (1998) indicates a velocity gradient within the galaxy along the same axis defined by the two star forming knots, while the nominal kinematic center more or less coincides with the reddest knot. The morphology of this object could suggest the merging of two dwarf galaxies before final relaxation or dynamical reconfiguration.
Salzer et al. (1989b) give a total B magnitude of 16.35 with B-R = 0.93, in acceptable agreement with our values: B = 16.18 and B-R = 0.73.
I SZ 59 (North down, East right): Described as "spherical'' by Rodgers et al. (1978), this object, in fact, is very elongated on our deep images, with regular elliptical outer isophotes. The central core has circular inner contours that become boxy at r = 6''. There is no isophote rotation. From the B-R color map, the starburst seems to be confined to the center of the galaxy. The surface brightness distribution is fitted with a r^1/4 law in the central region, whereas the light distribution in the envelope is fitted by an exponential with a shallow brightness gradient.
I SZ 399 (North down, East right): Described as "elliptical'' by [Rodgers et al.(1978)], this galaxy exhibits a regular structure except in the bright central core where a double nucleus is present. The environment of this double nucleus shows irregular contours with isophotal rotation. The central star forming region extends $\sim$ 500 pc across along the South-West direction. The surface brightness distribution is well represented by an exponential law, except in the central region (r $\le$ 7'') where a steep brightness gradient, perhaps caused by a bulge, is present.
II SZ 34 (North down, East right): this is an elliptical-like galaxy, in the NGC 5073 group, which is also close on the sky to an edge-on galaxy (MCG 2-34-24) showing strong absorption lines. The isophotes are disturbed and boxy. The central part of the galaxy shows a curved shape, and our B-R color map infers that the star forming region extends along the major axis. The surface brightness distribution is well fitted by a r^1/4 law, and a red envelope is seen from the B-R color excess.
13209-2723 (North down, East right): This compact elliptical-like galaxy was discovered in the ESO Prism Objective Survey ([Surace & Comte1994]). The galaxy shows a slightly off-centered star forming region. The surface brightness distribution is well fitted by a r^1/4 law in the B and R bands. The morphology is difficult to ascertain because of three foreground bright stars on top of the southern half of the galaxy.
Tololo 1434+032 (Fairall 42; North down, East right): this object looks like a Magellanic type galaxy with several star forming knots of red colors (from B-R $\sim$ 1.3 to 1.9). The B-R color map shows that the knots are connected to each other. The brightest knot is located at the center of the outer isophotes. At low surface brightness levels (26 mag/arcsec²), the B and R images show a red regular elliptical envelope, the major axis of which does not correspond to the major axis of the star forming region. The surface brightness distribution is neither a pure r^1/4 nor exponential law. There is a steep surface brightness gradient towards the center corresponding to the position of the brightest knot. The photometric decomposition of the surface brightness profile reveals the presence of two distinct components: an exponential component with a steep surface brightness gradient, and a low surface brightness underlying component fitted by a r^1/4 law (see Fig. 2c).
Bohuski et al. (1978) give B = 17.69 inside an aperture of 11.6'', in agreement with our measured B value of 18.10 mag in the same aperture.
Tololo 1448+116 (Fairall 44; North down, East right): it is another elliptical-like galaxy showing a star formation region distributed along the major axis. The brightest part of the galaxy has a reddish color of 0.9, and it is off-centered in the North-East direction. The isophotes are boxy without rotation. The surface brightness distribution is composite: a high surface brightness component, possibly a bulge, follows an r^1/4 law, and a faint surface brightness component, very shallow, is fitted by an exponential law. The color distribution shows a blueing of the external parts of the galaxy.

Table 5: Exponential galaxies: north and south samples

$\begin{tabular} {l c c c c c } \hline \multicolumn{1}{l}{Object} & \multicolumn{... ...l}{Scalelength in $B$\space and $R$\space are given kpc$^{-1}$.}\\ \end{tabular}$
Tololo 1924-416 (North down, East right): this BCDG is compact ( $r_{\rm eff}$ = 752 pc), luminous (M_B = -18.29) for a radius of r₂₆ = 3960 pc in B, and a color B-R = 0.90. An IRAS source ([Fehmers et al.1994]) has been detected at its position, indicating a significant amount of dust somewhere in the BCDG. However, the star formation region does not seem to contain much dust, according to a low Balmer decrement value H $_\alpha$ /H $_\beta$ of 3.1 ([Storchi-Bergmann et al.1995]). This galaxy shows many peculiar features: rotating disturbed isophotes, off-centered bright young star forming clusters. HST images ([Meurer et al.1995]) shows that the central SF region is resolved in very young star clusters. The B-R color map shows that the star formation occurs in the center of the galaxy, and that it is also spread along the major axis. The surface brightness distribution of the main galaxy is well fitted by a r^1/4 law for a surface brightness level fainter than 21 B mag/arcsec² (20.5 in R), whereas in the inner regions, the distribution is dominated by the central peak, that could be a bulge.
Tololo 1924-416 has a very faint neighbour (m_b = 17.8) separated by 142'' North-West from the BCDG (or 24 kpc, at the same distance). This galaxy looks like a Magellanic dwarf of low surface brightness with a B-R color of 1.3 similar to that of the UM 465 companion. The external isophotes of Tololo 1924-416 extend towards the faint object. The surface brightness distribution of the candidate companion can be fitted by an exponential law with large uncertainties in the fit due to a lower signal-to-noise. At the time this article was written, the nature of this neighbour was not known; since then, its recession velocity was measured by [Östlin et al.(1998)] confirming that it is indeed a companion of Tololo 1924-416.
In the contour plot of Tololo 1924-416 (in Fig. 1), we have removed the foreground galactic star located slightly off the center of the galaxy.
Tololo 1937-423 (North down, East right): this peculiar galaxy has lozenge isophotes. The central bright core contains a stellar nucleus of color B-R $\sim$ 0.6 and exhibits protruding radial extensions. The external envelope is also blue (B-R $\le$ 1.0). The surface brightness distribution is fitted by a r^1/4 law.

**Table 5:** Exponential galaxies: north and south samples
$\begin{tabular} {l c c c c c } \hline \multicolumn{1}{l}{Object} & \multicolumn{... ...l}{Scalelength in $B$\space and $R$\space are given kpc$^{-1}$.}\\ \end{tabular}$

3.6 The surface brightness distributions

In Paper I, we concluded that the 23 BCDGs from the Byurakan Surveys could be subdivided in three groups according to their surface brightness distribution: 10 objects clearly dominated by a "spheroidal'' component fitted by a dominant de Vaucouleurs (r^1/4) law, 7 objects clearly dominated by an exponential brightness distribution, and 6 composite or unclassifiable profiles. With this limited northern sample, we found that about 3/4 of our objects belong to the two first categories.

In the present sample, we find a similar repartition of our BCDGs in the three groups just defined: 12 objects are dominated by an exponential component (7 are fitted by a pure exponential law), 12 are dominated by a r^1/4 law (5 are fitted by a pure r^1/4 law). By "pure'' we mean that no other significant component has to be added to account for all the light of the galaxy. For the total sample of 44 Northern and Southern galaxies (1 companion included), we find that: 11 galaxies (25%) have SB profiles following closely a pure exponential distribution, and 8 (18%) galaxies with composite profiles in which the exponential component dominates; 9 galaxies (20%) have SB profiles following closely a pure r^1/4 distribution, and 12 galaxies (27%) with composite profiles in which the r^1/4 component dominates; finally, 3 galaxies are unclassifiable (7%), those peculiar galaxies are Mk 1499, Mk 1131 and SBS 1331+493 (Paper I).

Therefore, we support that the global structure of BCDGs, traced by their projected luminosity density, is not different, in terms of dynamical components, from the global structure in normal galaxies where two main stellar populations dominate. Those components are thick disks (whose true axial ratio distribution remains to be determined in the disk dominated BCDG galaxian population, see Sung et al. 1998), and spheroidal components obeying the r^1/4 law (implying a significant degree of relaxation). The present 20 disk-dominated BCDGs will be used to derive tight constraints on the true axial ratios of the disks, this will be treated in a following paper. In any case, kinematical data are also necessary, in addition to photometry of a larger sample of objects. Regarding the dynamics of the BCDGs, both exponential and r^1/4, we insist that a deeper analysis requires kinematical data from the gas and stellar populations.

The use of the light distribution to trace the mass distribution can be done to some extent, keeping in mind that the mass-to-light ratio usually varies within the galaxies, as indicated by the color gradient in BCDGs ([Papaderos et al.1996b]; [Doublier et al.1997] and this work). The central starburst dominated regions have mass-to-light ratio close to 0.1 ([Charlot et al.1996]) in the visual, while the outer old star population dominated regions ([Thuan1983]; [Hunter & Gallagher1985]; [Doublier et al.1999]) would have a mass-to-light ratio larger than 1. As a result, the mass distribution would flatten towards the center compared to the light distribution. Nevertheless, studies of the light profile in the near-infrared ([Doublier et al.1999]) shows that BCDGs with "optical'' r^1/4 law profiles display r^1/4 law profiles in the K band where the old stellar population dominates without a light excess in the central parts. This leads us to believe that the r^1/4 law is intrinsic, rather than being due to the light excess caused by the presence of the star formation regions.

**Table 6:** *r^1/4* galaxies; north and south samples
$\begin{tabular} {l r@{~$\pm$~}l r@{~$\pm$~}l c c c } \hline \multicolumn{1}{l}{O... ... 10.49&C \\ Mk 1426 & --& 8.92&0.09 & -- & 11.82& \\ \hline\hline\end{tabular}$

In Tables 5 and 6, we summarize the parameters derived from our photometric analysis. The surface brightness profiles were fitted uniquely either by a r^1/4 law or an exponential law. If neither case applies, a note in the last column of Tables 5 and 6 mentions that the surface brightness is "composite''.

The parameters of the exponential law and of the de Vaucouleurs (r^1/4) law were estimated using a crossed-linear regression applied to the regions that were not affected by the central "bulge-like'' component (in case of the exponential law) and seeing (in case of the de Vaucouleurs law), and excluding the outermost isophotes where the signal-to-noise ratio is too low. In a following section, we discuss the "extra'' components such as the central excess of light, or any possible excess of light present in the low S/N regions of the galaxies.

The excess of light in the central regions is probably due to the star forming regions: the method described by De Vaucouleurs (1959) we used to derive our surface photometry defines the center as the photometric center, while for ellipses fitting of the isophotes the center of the galaxy is defined as the center of last inner ellipse. We have tried the ellipses fitting on some of the most clumpy BCDGs in our sample, and the results are sensibly in agreement (within a few percent) in the outer regions, while the fit diverge considerably in the central regions.

The excess of light compared to a pure exponential law, or to the de Vaucouleurs law, seen in the outer parts of some BCDGs is not likely due to large errors (see surface brightness distributions in Fig. 1). In some cases, it could be attributed to an old, very low surface brightness component, whether this component could be exponential or r^1/4 is not clear. This component is detected in few cases (UM 465A, Fairall 301) in the near IR ([Doublier et al.1999]).

Figure 2 displays the surface brightness distributions of the r^1/4 BCDGs in the [ $\mu$ , $(r / r_{\rm eff})^{1/4}$ ] plane, where $\mu$ is the surface brightness in mag/arcsec², and $r_{\rm eff}$ the effective radius defined in Sect. 3.3.1 (a similar plot can be found in Paper I, for the northern sample). The plotted line represents the relations between the reduced radius and the surface brightness for a pure de Vaucouleurs law. Most of the r^1/4 profiles show a much steeper slope than the de Vaucouleurs relation. We discuss this difference in terms of the surface brightness gradient in the next section.

$\begin{figure} \includegraphics [width=8.5cm,clip]{figure3.ps} \includegraphics [width=8.5cm,clip]{figure3bc.ps} \end{figure}$

Figure 3: Relationship between the scale-length in B and R band. a) Relationship between de Vaucouleurs law slopes. The solid line represents the line of equal slopes in B and R. The relationship is obviously steeper than 1, the coefficients are systematically larger in B than in R, and systematically larger than the usual value 8.327. The large star represents the mean values of the subsample (10.0 in B and 9.7 in R) while the large triangle shows the empirical values of 8.327 in both bands. b) Relationship between the scale-lengths of the disk galaxies (or composite when the disk was easy to separate) in B and R bands. The solid line represents the line of equal scale lengths in B and R. The scale-lengths in both colors are clearly correlated. b, c) Variation of the $\chi^2$ as a function of the Equivalent. Radius. b) Variation of the $\chi^2$ for the elliptical-like galaxy: II SZ 34. The $\chi^2$ was obtained by dividing the surface brightness distribution modeled by the best fitting r^1/4 law, by the observed surface brightness distribution. Note the local maxima, in B and R, corresponding to inner features of the galaxy. c) $\chi^2$ variation for the disk galaxy: UM 465, obtained in the same way as above. Note the local maxima of the $\chi^2$ that are, unlikely to the elliptical case, behaving differently in B and R

3.6.1 "De Vaucouleurs'' profiles (23%)

Figure 3 (top panel) shows the relation between the observed slopes of the r^1/4 laws in reduced coordinates in R and B. The slope values are systematically larger than the canonical value of 8.327 for the law. Furthermore, the slopes are clearly larger in B than in R. This was also observed in our northern sample ([Doublier et al.1997]) for which we suggested either having systematically overestimated the effective radii or the presence of an homogeneous component in addition to the dominant spheroid. The systematic excess over the 8.327 value and the fact that this excess is larger in B than in R leads us to conclude that the presence of the starburst "component'' is probably responsible for this effect.

The most natural explanation is that the effective radius is overestimated. The overestimation of $r_{\rm eff}$ could result from errors in extrapolating the asymptotic magnitudes; however, we performed the surface photometry several times showing that the internal consistency of the asymptotic magnitude values is good. Then the excess $r_{\rm eff}$ values could result from the presence of a small compact component of a small scale length in the central part of the BCDG.

To investigate this hypothesis, we have simulated 3 types of galaxies: a pure elliptical, a dominant elliptical with a small additional r^1/4 central component, and a dominant elliptical with a small exponential central component. Seeing effects have been added by means of a convolution of the model galaxies with a Gaussian. The model images have subsequently been submitted to the surface photometry procedure, yielding a clear tendency to overestimate the resulting $r_{\rm eff}$ of the "Host galaxy + Starburst component'' whatever the nature of the starburst component.

To check the consistency of the fit to the r^1/4 law, we have performed $\chi^2$ tests by subtracting the model r^1/4 SB distribution that best fits from the observed SB. Figures 2b and 3c displays, as an example, the results on Mk 996 and II SZ 34 in B and R. The value of $\chi^2$ for II SZ 34 shows local maxima at 5, 15 and 30'' from the center, implying local significant departures from the pure r^1/4 law in these regions. These local departures originate from the fact that not all the star formation regions are concentrated in the central parts of the galaxies. This is commonly encountered in almost all "spheroidal'' BCDGs of our sample.

3.6.2 Exponential profiles (25%)

The mean value of the scale length parameter is 1.63 kpc^-1 without taking into account the scale length value of the first component of UM 461 (7.57 $\pm$ 0.1 (kpc^-1)) that may be due to the two very bright nuclei.

Figure 3 (bottom panel) shows the relation between the scale length in B and R. The relation shows that the scale lengths in B and R are well correlated. The disks should have similar stellar distribution in R and in B. In some cases, the B scale length is significantly larger than the R scale length.

Figures 3b and 3c show the $\chi^2$ variation for UM 465A, as a function of the equivalent radius, in B and R. As for the de Vaucouleurs profiles, the $\chi^2$ show small variations larger than the mean scale length that account for the existence of small structures within the disk of the galaxy: off-centered star formation regions, foreground faint stars, and globular clusters.

The disks and de Vaucouleurs parameters describing the galaxies are listed in Tables 5 and 6 respectively.

3.6.3 Composite profiles

We call "composite'' SB profiles that cannot be fitted by a pure exponential or a pure r^1/4 law. The shapes of these profiles (in B and R) can be very different from one galaxy to another. In most cases, two components are easily seen, the observed profiles being the sums of an exponential and a r^1/4, as in giant spirals, with one of these components being more or less dominant. However, for some other galaxies, the profiles displayed in the [ $r_{\rm e}$ , $\mu$ ] plane show a convex shape but when displayed in the [r^1/4, $\mu$ ]plane, the profiles exhibit a concave shape. Also, these galaxies show very disturbed isophotes. These systems may be relaxing merger remnants, or they could have a thick disk not yet settled inside a host elliptical galaxy.

Up: Multi-spectral study of a