

Up: Spectral classification of the systems
For M giants, the spectral type is strongly correlated with
mass loss, temperature, and
radius (see e.g. Reimers 1975; Dyck et al. 1996; Dumm & Schild 1998).
Stellar radius and mass loss are known to be
key parameters for triggering interaction phenomena in
binaries. As we have now a large
sample of accurate spectral types for the cool giants in symbiotic
systems at hand we can search for correlations with binary parameters
and outburst properties.
We searched the literature for orbital parameters. We found
orbital periods for about 30 systems whereas additional parameters are
less frequently determined. The periods are listed in Table 6.
About half of the
periods are determined from radial velocity measurements, the other
half is deduced from periodic brightness variations that are
supposed to be due to the binary revolution (see also Miko ajewska
1997).
ajewska
1997).
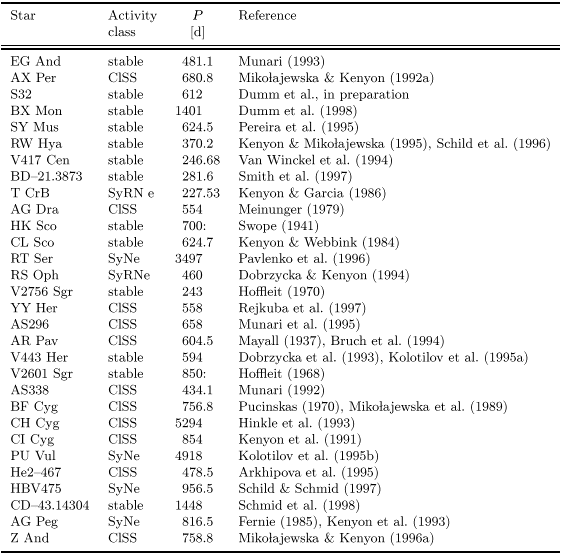
Table 6:
Published orbital periods of symbiotic systems. The
activity classes are labeled in the following way:
ClSS = Z And type outbursts (classical symbiotic variables);
SyNe = symbiotic novae; SyRNe = recurrent novae; stable =
no strong outburst is recorded (to our knowledge)
 |
![\begin{figure}
\includegraphics [width=8cm]{ds1672f7.ps}\end{figure}](/articles/aas/full/1999/12/ds1672/Timg64.gif) |
Figure 7:
Orbital periods as a function of the spectral type
of the cool binary components. The symbols denote different activity
classes: recurrent novae ( ), variables with Z And type outbursts ( ), variables with Z And type outbursts ( ),
symbiotic novae ( ),
symbiotic novae (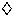 ), and objects without recorded strong
outbursts ( ), and objects without recorded strong
outbursts ( ). The full line markes the period limit discussed in the
text, the dashed line connects the relatively widest systems ). The full line markes the period limit discussed in the
text, the dashed line connects the relatively widest systems |
In Fig. 7 we plot the periods from Table 6
versus the respective spectral types from Table 5.
The shortest period system, at the lower right corner of the plot,
is the symbiotic recurrent nova T CrB. T CrB is an extra-ordinary
symbiotic, and we will discuss it further below.
Neglecting this object for the moment,
we discover that the systems that contain an M giant cluster
in Fig. 7 on a straight line. While there are some system above
this line, there is none far below. Therefore, the line
represents a minimum orbital period,  , for symbiotic systems of a
given spectral type. The line that is drawn in the figure
corresponds to the formula
, for symbiotic systems of a
given spectral type. The line that is drawn in the figure
corresponds to the formula

where S stands for the M subtype (e.g. S=3 for spectral type M3).
This limit can be interpreted in terms of binary geometry, because
the spectral type is related to the radius R of the giant and the
period is related to the binary
separation:
- -
- Radii of cool M giants of different
spectral subtypes are given by Dumm & Schild (1998). We adopted their
respective (median) values.
- -
- The orbital period is related to the binary separation through Kepler's
third law. Instead of the binary separation we computed the distance,
 , from the center of the cool star to the inner Lagrangian point
L1. For this we had to adopt a circular orbit and masses for
both stars. We adopted
, from the center of the cool star to the inner Lagrangian point
L1. For this we had to adopt a circular orbit and masses for
both stars. We adopted 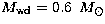 and
and
 for the hot and the cool components respectively.
These are typical values (see e.g.
Schmutz et al. 1994;
Schild et al. 1996).
An increase in the total mass would have the effect of
shifting
for the hot and the cool components respectively.
These are typical values (see e.g.
Schmutz et al. 1994;
Schild et al. 1996).
An increase in the total mass would have the effect of
shifting  to slightly larger values:
doubling the total mass, results in an increase of
to slightly larger values:
doubling the total mass, results in an increase of  by
by
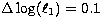 . Reversing the mass ratio has approximately
the same effect, but in the opposite direction.
. Reversing the mass ratio has approximately
the same effect, but in the opposite direction.
In Fig. 8 we show  vs. R for the systems of spectral
type M. The diagram looks still similar to Fig. 7 (except for
the confinement to spectral class M).
The three dashed lines indicate the locii
vs. R for the systems of spectral
type M. The diagram looks still similar to Fig. 7 (except for
the confinement to spectral class M).
The three dashed lines indicate the locii
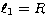 ,
, 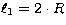 , and
, and 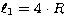 .
The systems clustering at the period limit are now
located close to
.
The systems clustering at the period limit are now
located close to 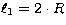 , with only T CrB far below.
Hence, the limit evidently corresponds to a configuration where the red
giant's photosphere reaches about half way out to L1:
, with only T CrB far below.
Hence, the limit evidently corresponds to a configuration where the red
giant's photosphere reaches about half way out to L1:
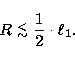
We therefore believe that the period limit is in fact a
restriction to
the radius of the red giant.
Under these conditions the system should be well detached.
If the photosphere of the cool giant further approaches the Lagrangian
critical surface the symbiotic phenomenon either disappears or becomes
short living. We speculate that dynamical mass exchange would start,
leading to an object that is no more regarded as a symbiotic star.
![\begin{figure}
\includegraphics [width=8cm]{ds1672f8.ps}\end{figure}](/articles/aas/full/1999/12/ds1672/Timg74.gif) |
Figure 8:
The distance of the inner Lagrangian point,  , versus the
cool star's radius, R, as determined from the spectral type, for
M-type systems. Symbols are as in Fig. 7.
The dotted lines denote , versus the
cool star's radius, R, as determined from the spectral type, for
M-type systems. Symbols are as in Fig. 7.
The dotted lines denote 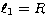 , , 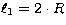 , and , and 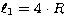 ,respectively ,respectively |
On the other hand, the cool star in T CrB,
according to Fig. 8, fills its Roche
lobe. This interpretation fits perfectly with its periodic light variations that are
attributed to the ellipsoidal shape of the red giant due to
the tidal distortions caused by the companion
(e.g. Belczynski & Miko ajewska 1998).
Strong ellipsoidal light variations are rarely observed for
symbiotic stars. T CrB is a peculiar symbiotic, in that it belongs at the
same time also to the class of recurrent novae with fast, large
amplitude outbursts. It differs also from other symbiotics
by the fact that the hot companion is more massive than the cool
giant. According to current mass transfer theories, this property
prevents dynamically unstable Roche lobe overflow from the cool giant
(see Belczynski & Miko
ajewska 1998).
Strong ellipsoidal light variations are rarely observed for
symbiotic stars. T CrB is a peculiar symbiotic, in that it belongs at the
same time also to the class of recurrent novae with fast, large
amplitude outbursts. It differs also from other symbiotics
by the fact that the hot companion is more massive than the cool
giant. According to current mass transfer theories, this property
prevents dynamically unstable Roche lobe overflow from the cool giant
(see Belczynski & Miko ajewska 1998).
A similar but much weaker ellipticity effect has also
been found in the light curve of EG And (Wilson & Vaccaro 1997).
This seems to suggest that
ajewska 1998).
A similar but much weaker ellipticity effect has also
been found in the light curve of EG And (Wilson & Vaccaro 1997).
This seems to suggest that 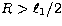 for this object
(e.g.
for this object
(e.g. 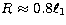 when adopting a large inclination
as expected for an eclipsing system) in contradiction with
Fig. 8. However, as discussed in Wilson & Vaccaro (1997)
such a large radius for the red giant is in contradiction with
current estimates for the distance of the EG And system.
One possible solution of this problem could be, that
radiation pressure lowers the effective surface gravity
of the red giant, so that the tidal distortions are
significantly enhanced and could therefore already be visible
for
when adopting a large inclination
as expected for an eclipsing system) in contradiction with
Fig. 8. However, as discussed in Wilson & Vaccaro (1997)
such a large radius for the red giant is in contradiction with
current estimates for the distance of the EG And system.
One possible solution of this problem could be, that
radiation pressure lowers the effective surface gravity
of the red giant, so that the tidal distortions are
significantly enhanced and could therefore already be visible
for  (see e.g. Drechsel et al. 1995).
(see e.g. Drechsel et al. 1995).
There exist systems with  ,but the symbiotic phenomena are possibly less pronounced unless
the wider separation is compensated by
another property (e.g. a higher luminosity of the white dwarf).
In terms of orbital period, the widest systems lie on the
dashed line in Fig. 7. This line corresponds to a
period
,but the symbiotic phenomena are possibly less pronounced unless
the wider separation is compensated by
another property (e.g. a higher luminosity of the white dwarf).
In terms of orbital period, the widest systems lie on the
dashed line in Fig. 7. This line corresponds to a
period
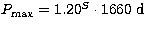 .
.
There is possibly a tendency for the classical symbiotic variables
(Z And type) to cluster closer to the  limiting ratio than
the symbiotic novae and those objects with less prominent outburst
activity.
limiting ratio than
the symbiotic novae and those objects with less prominent outburst
activity.


Up: Spectral classification of the systems
Copyright The European Southern Observatory (ESO)
![]() ajewska
1997).
ajewska
1997).

![]()
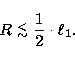
![]() ,but the symbiotic phenomena are possibly less pronounced unless
the wider separation is compensated by
another property (e.g. a higher luminosity of the white dwarf).
In terms of orbital period, the widest systems lie on the
dashed line in Fig. 7. This line corresponds to a
period
,but the symbiotic phenomena are possibly less pronounced unless
the wider separation is compensated by
another property (e.g. a higher luminosity of the white dwarf).
In terms of orbital period, the widest systems lie on the
dashed line in Fig. 7. This line corresponds to a
period
![]() .
.![]() limiting ratio than
the symbiotic novae and those objects with less prominent outburst
activity.
limiting ratio than
the symbiotic novae and those objects with less prominent outburst
activity.