

Up: IC348 proper motion study
With the available plate material we decided to carry out a photographic
photometry in addition to the main aim of the project which was the proper
motion study.
The instrumental magnitudes of all measured objects obtained by a
two-dimensional Gaussian fitting procedure (MRSP programme "profil'',
Horstmann et al. 1989) were transformed to the standard
system. This was done separately for each plate by using the CCD
UBVRI standards of Trullols & Jordi (1997). The standards
cover only the central region of the one square degree field around IC348
(see Fig. 1).
 |
Figure 1:
The one square degree field around IC348
selected for this study. Dots show all objects
with Gaussian image profile on at least three plates for which
proper motions have been determined.
Small circles show the location of the 38 bright stars in
the proper motion study of
Fredrick (1956).
The small dashed rectangle shows the region in which
Trullols & Jordi (1997) obtained UBVRI
photometry, the region shown by long dashed lines was
covered by NIR photometry (Lada & Lada 1995)
and the dashed circle shows the main field of ROSAT
observations (PSPC) used by
Preibisch et al.
(1996)
|
The transformation of the instrumental system to the standard system was
done by linear and quadratic polynomial fits using up to 60 standard stars.
Unfortunately, we were not able to determine a proper colour equation
for this transformation. An attempt to determine the colour term
after first fitting the instrumental magnitudes on plate sj01520 with the B
standard magnitudes and then investigating the residual magnitude differences
as a function of the B-V colours given by Trullols & Jordi
(1997) did not yield satisfactory results.
The colour equation
| 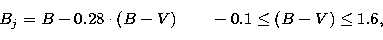 |
(1) |
given by Blair & Gilmore (1982) could not be used,
since only 12 bright stars out of the 43 standard stars have colours in
the range 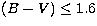 .
.
The photographic photometry on the Schmidt plates was a priori
expected to be difficult since the central region of IC 348,
where the standard stars are located (Fig. 1), is strongly
affected
by image crowding from bright stars and nebulosities. Moreover, as is
obvious from the inspection of Fig. 1,
there is strong extinction which is irregularly distributed
over the field. Thus, the adopted transformation between the
instrumental system to the standard system is only of moderate accuracy.
In Table 2, the dispersions of the differences
between standard magnitudes and fitted magnitudes of all stars used in
the fitting procedure are listed. The Tautenburg plates provide a somewhat
higher accuracy due to their better scale but have a brighter limiting
magnitude (the blue Palomar plate goes about 2.0 magnitudes fainter compared
to the two blue Tautenburg plates).
Table 2:
Photometric calibration
- [
 ] 1 = linear, 2 = quadratic polynomial fit. ] 1 = linear, 2 = quadratic polynomial fit.
- [
 ] Dispersion of magnitude differences (standard - fitted). ] Dispersion of magnitude differences (standard - fitted).
- [
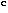 ] Fit consisted of two straight lines for R < 16 and R > 16. ] Fit consisted of two straight lines for R < 16 and R > 16.
|
Comparing the B magnitudes obtained from the Tautenburg plates 9168 and
9177 with the Bj magnitudes obtained from the Palomar plate sj01520,
we found large systematic differences (see Figs. 2a
and 2b), especially for the bright stars (B < 17).
At least a part of these differences is expected to arise from the moderate
accuracy
of the calibration procedure described above, especially from the omission of
the colour term. As a test, we applied the colour equation from Eq. (1)
but could not remove the systematic difference between the Palomar and
Tautenburg B magnitudes.
A further source of the differences may be the smaller number of bright
(B < 16.5) standards used in
the calibration of the blue Palomar plate (5 stars) compared to the
blue Tautenburg plates (9 stars) and the relatively large error of the
magnitude calibration for plate sj01520 (see Table 2).
The systematic deviation of the Palomar Bj from the Tautenburg B
magnitudes is very similar for both Tautenburg plates. Therefore, we
have obtained a simple transformation of the Palomar Bj
magnitudes into the system of the mean B magnitudes of the Tautenburg
plates
| 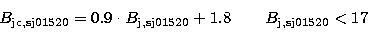 |
(2) |
from a linear polynomial fit using the stars with  measured as well on both Tautenburg B plates.
For the faint stars (
measured as well on both Tautenburg B plates.
For the faint stars (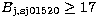 ) we have
not applied any correction, since the Tautenburg B magnitudes
become unreliable at
) we have
not applied any correction, since the Tautenburg B magnitudes
become unreliable at 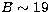 (only one standard star with B > 19
was used in the calibration), whereas there were still about 20 standard stars
with 19 < B < 21.5 used in the calibration of the blue Palomar plate.
(only one standard star with B > 19
was used in the calibration), whereas there were still about 20 standard stars
with 19 < B < 21.5 used in the calibration of the blue Palomar plate.
Table 3:
Internal photometric accuracy for blue and red plates
described by the standard deviation of magnitude
differences after the correction of the Bj and
E magnitudes (Eq. (2) and (3))
had been applied
- [
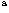 ] ] 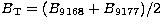 , , 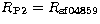 . . - [
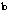 ] Number of common stars in given magnitude interval. ] Number of common stars in given magnitude interval.
|
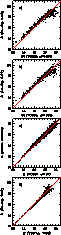 |
Figure 2:
Plate-to-plate comparison of calibrated photographic
magnitudes (the solid lines
indicate zero magnitude differences): a) and b)
comparison of B magnitudes obtained on the Tautenburg
plates with Bj magnitudes obtained on the POSS2 plate, c)
comparison of POSS1 E and POSS2 R plates, d) Comparison
of two Tautenburg B plates. Figuresa), b) and c) show
the original calibrated magnitudes before the corrections
(Eqs. (2) and (3)), respectively for the
Bj and E magnitudes had been applied
|
Figures 2a and 2b show the result before the
correction of Bj had been applied. In Fig. 2d the B
magnitudes obtained from the two Tautenburg B plates are compared.
The internal accuracy of the blue magnitudes obtained from two Tautenburg
B plates and one Palomar Bj plate can be described by the standard
deviation of the magnitude differences (see Table 3).
For the two Tautenburg B plates we obtained a mean B magnitude
difference (B9168-B9177) of +0.00 with a standard deviation
of 0.27mag over the whole magnitude interval. After
excluding the obviously bad measured/calibrated faint stars on the
Tautenburg B plates (B > 18, as
can be seen from Fig. 2d) we obtained a much better accuracy
(0.13mag standard deviation). The general trend in
Figs. 2a and 2b
can be roughly explained as follows: According to Eq. (1),
the Tautenburg
B is expected to be a few tenth mag fainter than Bj for typical
(B-V). The apparent turnoff of the 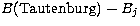 relation at
fainter magnitudes is likely due to a selection effect near the
Tautenburg plate limit. Stars scattered, at fixed Bj, below the mean
relation, due to the colour equation and/or due to measuring errors,
will be measured on both the Tautenburg plate and the Palomar plate.
However, stars scattered above the mean relation will be missed,
in general, on the Tautenburg plates.
relation at
fainter magnitudes is likely due to a selection effect near the
Tautenburg plate limit. Stars scattered, at fixed Bj, below the mean
relation, due to the colour equation and/or due to measuring errors,
will be measured on both the Tautenburg plate and the Palomar plate.
However, stars scattered above the mean relation will be missed,
in general, on the Tautenburg plates.
The standard deviation of the differences between the corrected Bj and
the mean Tautenburg B magnitudes is still the largest value among all
possible plate-to-plate comparisons shown in Table 3. But it is
better than one could expect from the accuracies of the external calibrations
given in Table 2.
Between the E and R magnitudes obtained, respectively from the red
POSS1 and POSS2 plates there are also small systematic deviations.
The E magnitudes of the POSS1 plate e1457 can be transformed to
the system of the POSS2 R plate by Eq. (3).
| 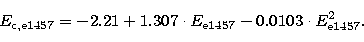 |
(3) |
Figure 2c shows the comparison between the red magnitudes
before the transformation of the POSS1 E magnitudes to the system
of the POSS2 R plate given by Eq. (3) had been applied.
After the correction of Eq. (3) we obtained, as an estimate of the
internal magnitude accuracy, the mean difference ( )
and its dispersion over the whole magnitude interval (see Table 3).
The dispersion decreases not as strong as for the two
Tautenburg B plates if only the bright stars (R < 16) are considered.
)
and its dispersion over the whole magnitude interval (see Table 3).
The dispersion decreases not as strong as for the two
Tautenburg B plates if only the bright stars (R < 16) are considered.
 |
Figure 3:
Proper motion errors as a function of magnitude a) for
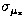 and b) for and b) for 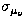 . The
dashed lines show the mean errors as obtained from a
second order polynomial fit in case of . The
dashed lines show the mean errors as obtained from a
second order polynomial fit in case of 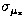 and from a third order polynomial fit in case of and from a third order polynomial fit in case of
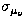 . The solid lines show the magnitude
dependent proper motion dispersions . The solid lines show the magnitude
dependent proper motion dispersions
 and and 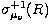 (obtained from adding
1mas/yr to the mean errors) which were used in the
determination of membership probabilities by Eq. (4) (obtained from adding
1mas/yr to the mean errors) which were used in the
determination of membership probabilities by Eq. (4)
|


Up: IC348 proper motion study
Copyright The European Southern Observatory (ESO)




