The temperature dependent rate coefficient ![]() for a transition
between atomic levels with indices i and j and energy separation Eij
is given in terms of the effective, or thermally averaged, collision strength
for a transition
between atomic levels with indices i and j and energy separation Eij
is given in terms of the effective, or thermally averaged, collision strength
![]() by
by
![]()
| (1) |
Following Seaton (1953) we define the effective collision strength
![]() as follows:
as follows:
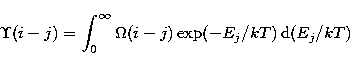 |
(2) |
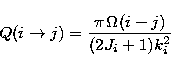 |
(3) |
Eighteen years ago Bhatia & Mason (1981) used W.B. Eissner's distorted wave
collision code, which originated at University College London, to calculate
collision strengths for many transitions in ![]() .
Five years later Bhatia & Mason (1986) extended their work to energies both
below and above those they considered in 1981; they gave a comprehensive
tabulation covering the interval from 15 to 350 Ry. In order to carry out
thermal averaging Bhatia & Mason (1986) linearly interpolated their data and
integrated the resulting function
.
Five years later Bhatia & Mason (1986) extended their work to energies both
below and above those they considered in 1981; they gave a comprehensive
tabulation covering the interval from 15 to 350 Ry. In order to carry out
thermal averaging Bhatia & Mason (1986) linearly interpolated their data and
integrated the resulting function ![]() analytically (Mason 1998, private communication) in order to obtain
analytically (Mason 1998, private communication) in order to obtain
![]() .
Corliss & Sugar (1982) estimate the ionization energy of the ground state
to be 15797000
.
Corliss & Sugar (1982) estimate the ionization energy of the ground state
to be 15797000 ![]() (143.95 Ry), which means that three of
Bhatia
& Mason's (1986) energies lie above the ionization threshold while the rest
are below. Since Bhatia & Mason (1981) include a thorough discussion
of collision calculations devoted to
(143.95 Ry), which means that three of
Bhatia
& Mason's (1986) energies lie above the ionization threshold while the rest
are below. Since Bhatia & Mason (1981) include a thorough discussion
of collision calculations devoted to ![]() up to the time of
their own investigation, the reader is encouraged to consult their paper for
information on this ion and we shall refrain from giving further
details here except for a list of relevant papers in Table 1.
up to the time of
their own investigation, the reader is encouraged to consult their paper for
information on this ion and we shall refrain from giving further
details here except for a list of relevant papers in Table 1.
Copyright The European Southern Observatory (ESO)