![\begin{figure}
\includegraphics [angle=-90,width=8cm]{pl_flux.ps}\end{figure}](/articles/aas/full/1999/09/ds1597/Timg17.gif) |
Figure 1: The histograph for the flux comparison. Some pulsars (e.g. these in Table 1) have been missed in the left-half of the distribution (i.e. when Snvss/Spsrcat<1), because scintillation makes them weaker than the NVSS sensitivity |
![\begin{figure}
\includegraphics [angle=-90,width=8cm]{pl_flux.ps}\end{figure}](/articles/aas/full/1999/09/ds1597/Timg17.gif) |
Figure 1: The histograph for the flux comparison. Some pulsars (e.g. these in Table 1) have been missed in the left-half of the distribution (i.e. when Snvss/Spsrcat<1), because scintillation makes them weaker than the NVSS sensitivity |
The VLA measurements of the flux densities
S1.4 of most identified pulsars, averaged
over about 84 MHz bandwidth and 3![]() 23 s in time, are comparable
to the flux densities published in
Lorimer et al. (1995) and
Gould & Lyne (1998). They are generally within a factor of 2 of the
published densities (see Fig. 1), but sometimes
up to a factor of 3 or more. Most of undetected pulsars (
23 s in time, are comparable
to the flux densities published in
Lorimer et al. (1995) and
Gould & Lyne (1998). They are generally within a factor of 2 of the
published densities (see Fig. 1), but sometimes
up to a factor of 3 or more. Most of undetected pulsars (![]() 400)
have flux densities below 2 or 3 mJy. Interstellar scintillation
(e.g.
Gupta et al. 1994) both helps and hinders the detections
(Cordes & Lazio 1991). Some pulsars which have a flux density less than
2 mJy in the pulsar catalog have been detected in the NVSS with a larger flux density.
The scintillation effect is more obvious for strong pulsars. For example, PSR B2020+28
should be as strong as 38.0 mJy, but in the NVSS it appears to be a highly polarized
source of
400)
have flux densities below 2 or 3 mJy. Interstellar scintillation
(e.g.
Gupta et al. 1994) both helps and hinders the detections
(Cordes & Lazio 1991). Some pulsars which have a flux density less than
2 mJy in the pulsar catalog have been detected in the NVSS with a larger flux density.
The scintillation effect is more obvious for strong pulsars. For example, PSR B2020+28
should be as strong as 38.0 mJy, but in the NVSS it appears to be a highly polarized
source of ![]() mJy. Among 61 pulsars with known flux densities larger than 5 mJy, about one fourth
were missed by the NVSS (as listed in Table 2), some due to scintillation,
some due to confusion (Condon, private communication).
mJy. Among 61 pulsars with known flux densities larger than 5 mJy, about one fourth
were missed by the NVSS (as listed in Table 2), some due to scintillation,
some due to confusion (Condon, private communication).
When pulsars are observed as continuum radio sources, the polarized
intensity, L, and polarization position angle, PA, are calculated
from the integrated Q and U values of the final images, i.e., over
all the observation time and the bandwidth, so that
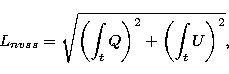 |
(1) |
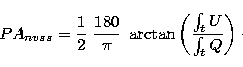 |
(2) |
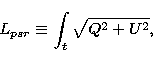 |
(3) |
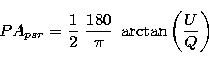 |
(4) |
Since the NVSS
has very accurate absolute position angle calibrations (![]() ),
the well measured PA of a few pulsars (with error
),
the well measured PA of a few pulsars (with error ![]() ) may
help to make an absolute PA calibration in pulsar observations.
One example is shown in Fig. 3. First, using the VLA measurements of
PA at 1400 MHz and the RM values, we calculated the averaged PA over
the pulse at the observation frequency accordingly. Second, from the
pulsar observations, we got PA for calibration pulsars using Eq. (2)
from the pulse profiles (including interpulse if applicable) of Stokes
parameters Q and U. Third we compared them to get an offset which
represents the instrument PA offset, and used it to calibrate all pulsar
observations.
) may
help to make an absolute PA calibration in pulsar observations.
One example is shown in Fig. 3. First, using the VLA measurements of
PA at 1400 MHz and the RM values, we calculated the averaged PA over
the pulse at the observation frequency accordingly. Second, from the
pulsar observations, we got PA for calibration pulsars using Eq. (2)
from the pulse profiles (including interpulse if applicable) of Stokes
parameters Q and U. Third we compared them to get an offset which
represents the instrument PA offset, and used it to calibrate all pulsar
observations.
![\begin{figure}
\includegraphics [angle=-90,width=8.5cm]{1929.ps}\end{figure}](/articles/aas/full/1999/09/ds1597/Timg31.gif) |
Figure 3: Calibration for absolute polarization angle. Pulsar data were observed by von Hoensbroech & Xilouris (1997). In the lower panel, the total intensity, I, and linearly polarized intensity, L, are plotted with a thick continuum line and a dot-dash line, respectively. (The interpulse is almost 100% polarized.) In the top panel, the original PA data are plotted with a thin line (and with an error bar on every second point), and the calibrated PA data are plotted with a thick line |
In Table 3, we listed 5 pulsars which can be used for calibration purposes.
All of them have strong linear polarized intensity that can be easily detected,
and their rotation measures RM are either quite small (![]() 10 rad m-2)
or accurately measured (
10 rad m-2)
or accurately measured (![]() rad m-2). None of them
has any mode-changing (e.g. PSR B1237+25 and PSR B1822+09) or complicated
variations in PA across the profile (e.g. PSR B1933+16). All pulsars in
Table 3 satisfy
rad m-2). None of them
has any mode-changing (e.g. PSR B1237+25 and PSR B1822+09) or complicated
variations in PA across the profile (e.g. PSR B1933+16). All pulsars in
Table 3 satisfy ![]() , where
, where ![]() was the difference of the
wavelengths squared, and was taken as 1.0.
was the difference of the
wavelengths squared, and was taken as 1.0.
Pulsar proper motion is a very important quantity to be measured, so that pulsar velociaties can be determined. Pulsar timing can be used to determine the proper motions of millisecond pulsars because of their great timing stability (e.g. Nice & Taylor 1995). However, for most pulsars, the proper motions can only be measured by determining the pulsar position precisely at two or more well-separated epochs using interferometry (e.g. Fomalont et al. 1997).
We compared the pulsar positions given in the pulsar catalog with those from the NVSS whose epoch is simply taken as MJD = 49718, and calculated pulsar proper motions if possible. The results are listed in Table 4. Pulsars with uncertainties of proper motion larger than 200 mas yr-1 have been deleted. Because of the large uncertainty of the NVSS positions, we obtained only a few significant measurements: proper motion in declination direction of PSR B1133+16, and that in right ascension of PSRs B0823+26 and B2016+28. While the former two are consistent with the previous measurements made by Lyne et al. (1982), the latter one is marginally not. Cross-checking with Table 2 of Taylor et al. (1993), we found that all other measurements in Table 4 are consistent with (though poorer than) those given in the pulsar catalog, except for one new upper limit of PSR B0031-07. VLA A-array observations of these pulsars in Table 1 should provide much more accurate positions, and hence could produce the first measurement of the proper motions of about 20 pulsars.
PSR B0031-07 is a nearby pulsar with distance 0.68 kpc. Its proper
motion upper limit indicates that the pulsar has a velocity of
![]() km s-1, quite normal according to the pulsar velocity
distribution (Lyne & Lorimar 1994).
km s-1, quite normal according to the pulsar velocity
distribution (Lyne & Lorimar 1994).
Copyright The European Southern Observatory (ESO)