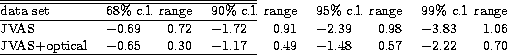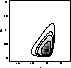
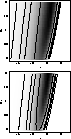
Figure 3:
Left column: The posterior probability density
functions 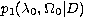 (top panel), (top panel),
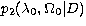 (middle panel) and (middle panel) and
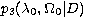 (bottom panel). All nuisance parameters are
assumed to take precisely their mean values. The pixel grey level is
directly proportional to the likelihood ratio, darker pixels reflect
higher ratios. The pixel size reflects the resolution of our numerical
computations. The contours mark the boundaries of the minimum 0.68,
0.90, 0.95 and 0.99 confidence regions for the parameters (bottom panel). All nuisance parameters are
assumed to take precisely their mean values. The pixel grey level is
directly proportional to the likelihood ratio, darker pixels reflect
higher ratios. The pixel size reflects the resolution of our numerical
computations. The contours mark the boundaries of the minimum 0.68,
0.90, 0.95 and 0.99 confidence regions for the parameters
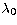 and and 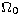 . The respective amounts of information
obtained from our sample data are I1=1.42, I2=1.32 and I3=1.45.
Right column: Exactly the same as the left panel, but the joint
likelihood from the JVAS lens sample and the optical samples from
Quast & Helbig (1999). The respective amounts of information
obtained from our joint sample data are 1.98, 1.95 and 1.96. See
Paper I for definitions . The respective amounts of information
obtained from our sample data are I1=1.42, I2=1.32 and I3=1.45.
Right column: Exactly the same as the left panel, but the joint
likelihood from the JVAS lens sample and the optical samples from
Quast & Helbig (1999). The respective amounts of information
obtained from our joint sample data are 1.98, 1.95 and 1.96. See
Paper I for definitions
The left plot in the top row of Fig. 3 shows the joint
likelihood of our lensing statistics analysis and that obtained by using
conservative estimates for H0 and the age of the universe (see
Paper I). Although neither method alone sets useful constraints on
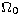 , their combination does, since the constraint from H0
and the age of the universe
only allows large values of , their combination does, since the constraint from H0
and the age of the universe
only allows large values of 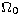 for for 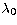 values which
are excluded by lens statistics. Even though the 68% confidence
contour still allows almost the entire values which
are excluded by lens statistics. Even though the 68% confidence
contour still allows almost the entire 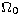 range, it is obvious
from the grey scale that much lower values of range, it is obvious
from the grey scale that much lower values of 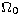 are favoured
by the joint constraints. The upper limit on are favoured
by the joint constraints. The upper limit on 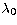 changes only
slightly while, as is to be expected, the lower limit becomes tighter.
Right plot: exactly the same, but including optical constraints from
Paper I. The upper limits on changes only
slightly while, as is to be expected, the lower limit becomes tighter.
Right plot: exactly the same, but including optical constraints from
Paper I. The upper limits on 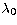 decrease slightly, while the
lower limits improve considerably. The latter is probably due to the
fact that, in addition to just using more data the JVAS sources are at
significantly different redshifts than those from the optical surveys
analysed in Paper I (the JVAS sources are generally at lower redshift).
The former is consistent with the slightly higher optical depth for
radio surveys found by FKM and will be discussed more below. decrease slightly, while the
lower limits improve considerably. The latter is probably due to the
fact that, in addition to just using more data the JVAS sources are at
significantly different redshifts than those from the optical surveys
analysed in Paper I (the JVAS sources are generally at lower redshift).
The former is consistent with the slightly higher optical depth for
radio surveys found by FKM and will be discussed more below.
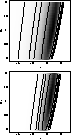
The middle row of Fig. 3 shows the effect of including
our prior information on 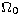 (see Paper I). As is to be
expected, (for both the JVAS and combination data sets) lower values of (see Paper I). As is to be
expected, (for both the JVAS and combination data sets) lower values of
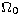 are favoured. This has the side effect of weakening our
lower limit on are favoured. This has the side effect of weakening our
lower limit on 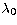 (though only slightly affecting the upper
limit). This should not be regarded as a weakness, however, since
including prior information for (though only slightly affecting the upper
limit). This should not be regarded as a weakness, however, since
including prior information for 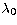 and and 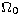 from the
constraint from H0 and the age of the universe as well as for from the
constraint from H0 and the age of the universe as well as for
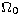 itself, as illustrated in the bottom row of
Fig. 3, tightens the lower limit again (without
appreciably affecting the upper limit). itself, as illustrated in the bottom row of
Fig. 3, tightens the lower limit again (without
appreciably affecting the upper limit).
We believe that the right plot of the bottom row of
Fig. 3 represents very robust constraints in the
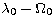 plane. The upper limits on plane. The upper limits on 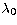 come from gravitational lensing statistics, which, due to the extremely
rapid increase in the optical depth for larger values of come from gravitational lensing statistics, which, due to the extremely
rapid increase in the optical depth for larger values of 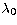 ,are quite robust and relatively insensitive to uncertainties in the
input data (cf. Fig. 2 and the discussion of the
effect of changing the most uncertain input parameter by 2 ,are quite robust and relatively insensitive to uncertainties in the
input data (cf. Fig. 2 and the discussion of the
effect of changing the most uncertain input parameter by 2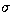 in
Paper I) as well as to the prior information used (compare the upper,
lower and middle rows of Fig. 3). The combination of
data from JVAS and optical surveys leads to much tighter lower limits on in
Paper I) as well as to the prior information used (compare the upper,
lower and middle rows of Fig. 3). The combination of
data from JVAS and optical surveys leads to much tighter lower limits on
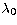 than using either alone. The upper and lower limits on than using either alone. The upper and lower limits on
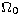 are based on a number of different methods and appear to be
quite robust (see Paper I). The combination of the relatively secure
knowledge of H0 and the age of the universe combine with lens
statistics to produce a good lower limit on are based on a number of different methods and appear to be
quite robust (see Paper I). The combination of the relatively secure
knowledge of H0 and the age of the universe combine with lens
statistics to produce a good lower limit on 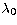 , although this
is to some extent still subject to the caveats mentioned above. , although this
is to some extent still subject to the caveats mentioned above.
If one is interested in the allowed range of 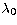 , one can
marginalise over , one can
marginalise over 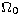 to obtain a probability distribution for to obtain a probability distribution for
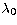 . This is illustrated in Fig. 4 . This is illustrated in Fig. 4
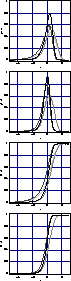 |
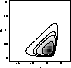
Figure 4:
Left column: The top panel shows the normalised
marginal likelihood function 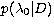 (light gray curve) and the
marginal posterior probability density functions (light gray curve) and the
marginal posterior probability density functions 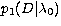 (medium gray curve), (medium gray curve), 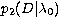 (dark gray curve) and (dark gray curve) and
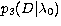 (black curve) derived from the JVAS analysis. All
nuisance parameters are assumed to take precisely their mean values.
The bottom panel shows the respective cumulative distribution functions.
Right column: Exactly the same as the left panel, but the joint
likelihood from the JVAS lens sample and the optical samples from
Quast & Helbig (1999) (black curve) derived from the JVAS analysis. All
nuisance parameters are assumed to take precisely their mean values.
The bottom panel shows the respective cumulative distribution functions.
Right column: Exactly the same as the left panel, but the joint
likelihood from the JVAS lens sample and the optical samples from
Quast & Helbig (1999) |
and Table 2.
Table 2:
Marginal mean values, standard deviations and 0.95
confidence intervals for the parameter 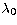 on the basis of the
marginal distributions shown in the top row of Fig. 4 on the basis of the
marginal distributions shown in the top row of Fig. 4
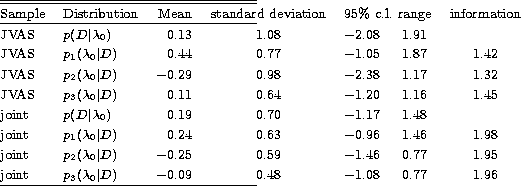 |
The comparison values from this work corresponding to those in Tables 3
and 4 of Paper I are presented in Tables 3 and
4.
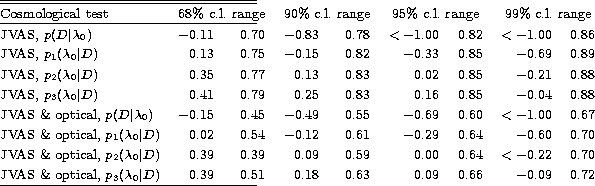
Table 3:
Mean values and ranges for assorted confidence levels for the
parameter 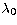 for our a priori and various a posteriori
likelihoods from this work for for our a priori and various a posteriori
likelihoods from this work for 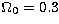 . This should be
compared to Table 3 in Paper I . This should be
compared to Table 3 in Paper I
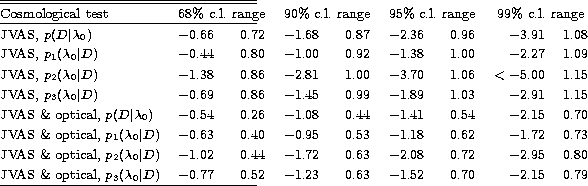 |
Table 4:
Mean values and ranges for assorted confidence levels for the
parameter 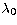 for our a priori and various a posteriori
likelihoods from this work for k=0. This should be compared to
Table 4 in Paper I for our a priori and various a posteriori
likelihoods from this work for k=0. This should be compared to
Table 4 in Paper I
 |
For a "likely'' 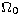 value of 0.3 we have calculated the
likelihood with the higher resolution value of 0.3 we have calculated the
likelihood with the higher resolution 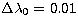 . This is
show in Fig. 5. . This is
show in Fig. 5.
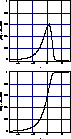 |
Figure 5:
Left panel: The likelihood function as a function of
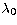 for for 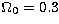 and with all nuisance parameters
taking their default values, using just the JVAS data. Right
panel: The same but plotted cumulatively and with all nuisance parameters
taking their default values, using just the JVAS data. Right
panel: The same but plotted cumulatively |
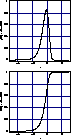 |
Figure 6:
As Fig. 5 but combining optical and radio data.
Left panel: The likelihood function as a function of
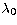 for for 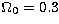 and with all nuisance parameters
taking their default values. Right panel: The same but plotted
cumulatively and with all nuisance parameters
taking their default values. Right panel: The same but plotted
cumulatively |
From these calculations one can extract confidence limits which, due to
the higher resolution in 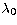 , are more accurate. These are
presented in Table 5 and should be compared to those for , are more accurate. These are
presented in Table 5 and should be compared to those for
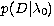 from Table 3. from Table 3.
Table 5:
Confidence ranges for 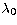 assuming assuming
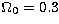 . Unlike the results presented in
Table 3, these figures are for a specific value of . Unlike the results presented in
Table 3, these figures are for a specific value of
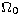 and not the values of intersection of particular contours
with the and not the values of intersection of particular contours
with the 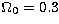 line in the line in the 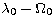 plane.
These are more appropriate if one is convinced that plane.
These are more appropriate if one is convinced that 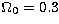 and
have been calculated using ten times better resolution than the rest of
our results presented in this work. See Figs. 5 and
6 and
have been calculated using ten times better resolution than the rest of
our results presented in this work. See Figs. 5 and
6
 |
As mentioned in Paper I, to aid comparisons with other cosmological
tests, the data for the figures shown in this paper are available at
http://multivac.jb.man.ac.uk:8000/ceres
/data_from_papers/JVAS.html
and we urge our colleagues to follow our example.


Up: Gravitational lensing statistics with
Copyright The European Southern Observatory (ESO)
|


![]() (see Paper I). As is to be
expected, (for both the JVAS and combination data sets) lower values of
(see Paper I). As is to be
expected, (for both the JVAS and combination data sets) lower values of
![]() are favoured. This has the side effect of weakening our
lower limit on
are favoured. This has the side effect of weakening our
lower limit on ![]() (though only slightly affecting the upper
limit). This should not be regarded as a weakness, however, since
including prior information for
(though only slightly affecting the upper
limit). This should not be regarded as a weakness, however, since
including prior information for ![]() and
and ![]() from the
constraint from H0 and the age of the universe as well as for
from the
constraint from H0 and the age of the universe as well as for
![]() itself, as illustrated in the bottom row of
Fig. 3, tightens the lower limit again (without
appreciably affecting the upper limit).
itself, as illustrated in the bottom row of
Fig. 3, tightens the lower limit again (without
appreciably affecting the upper limit).
![]() plane. The upper limits on
plane. The upper limits on ![]() come from gravitational lensing statistics, which, due to the extremely
rapid increase in the optical depth for larger values of
come from gravitational lensing statistics, which, due to the extremely
rapid increase in the optical depth for larger values of ![]() ,are quite robust and relatively insensitive to uncertainties in the
input data (cf. Fig. 2 and the discussion of the
effect of changing the most uncertain input parameter by 2
,are quite robust and relatively insensitive to uncertainties in the
input data (cf. Fig. 2 and the discussion of the
effect of changing the most uncertain input parameter by 2![]() in
Paper I) as well as to the prior information used (compare the upper,
lower and middle rows of Fig. 3). The combination of
data from JVAS and optical surveys leads to much tighter lower limits on
in
Paper I) as well as to the prior information used (compare the upper,
lower and middle rows of Fig. 3). The combination of
data from JVAS and optical surveys leads to much tighter lower limits on
![]() than using either alone. The upper and lower limits on
than using either alone. The upper and lower limits on
![]() are based on a number of different methods and appear to be
quite robust (see Paper I). The combination of the relatively secure
knowledge of H0 and the age of the universe combine with lens
statistics to produce a good lower limit on
are based on a number of different methods and appear to be
quite robust (see Paper I). The combination of the relatively secure
knowledge of H0 and the age of the universe combine with lens
statistics to produce a good lower limit on ![]() , although this
is to some extent still subject to the caveats mentioned above.
, although this
is to some extent still subject to the caveats mentioned above.
![]() , one can
marginalise over
, one can
marginalise over ![]() to obtain a probability distribution for
to obtain a probability distribution for
![]() . This is illustrated in Fig. 4
. This is illustrated in Fig. 4




![]() value of 0.3 we have calculated the
likelihood with the higher resolution
value of 0.3 we have calculated the
likelihood with the higher resolution ![]() . This is
show in Fig. 5.
. This is
show in Fig. 5.