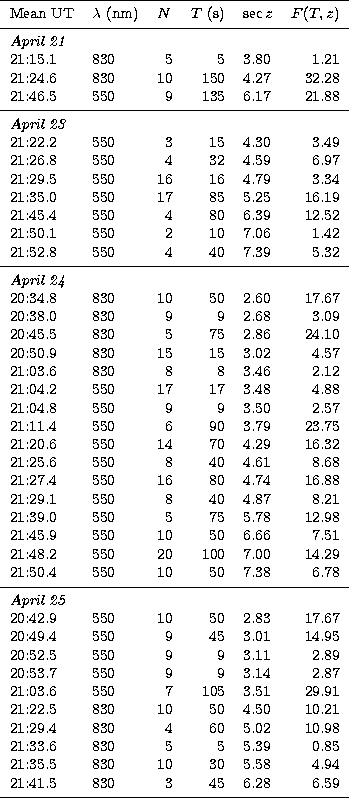
Details of the data set is given in Table 2, where F(T, z) is a relative measure of the flux recorded by the detector in the direction of the comet photo-centre at sky conditions characteristic of the observing period. Its value is given by

$\begin{displaymath} F(T, z) = Tk_\lambda\,\sec z\end{displaymath}$

(1)

where T is the total exposure time in seconds and z the zenithal distance of the comet in degrees. The factor k₅₅₀ = 1 or k₈₃₀ = 0.919 corrects for the respective filter band-passes, total transmissions and CCD quantum efficiency. For a one second exposure towards the zenith through the $\lambda~550\ \rm nm$ filter, the CCD thus records a relative flux level of unity.

**Table 2:** Observational dataset. N is number of images added for each mean UT, T is total exposure time, z is zenithal distance and F is a measure of the relative recorded flux as described in the text
$\begin{tabular} {llrrlr} \hline \noalign{\smallskip} \multicolumn{1}{l}{ Mea... ...5 & 830 & 3 & 45 & 6.28 & 6.59 \\ \noalign{\smallskip} \hline \end{tabular}$

Alignment of the images prior to addition was made to 0.1 pixel ( $0\hbox{$.\!\!^{\prime\prime}$}03$ ) accuracy. The alignment was performed with a MIDAS procedure using an intensity weighted first moment of the pixel values within a square aperture to compute the central position of the object. The aperture varied in size between $13-26\hbox{$^{\prime\prime}$}$ depending on image brightness. Several overlapping fields containing the approximate photo-centre location were sampled whereby photo-centre positions were obtained. The positions were averaged to determine mean pixel coordinates of the photo-centre. Images with the same exposure time were then added based on these coordinates. After flat- and dark-correction, alignment and addition, the frames were cropped to $512\times512$ pixel ( $123''\times123''$ ) size symmetric to the photo-centre and remaining cosmetic blemishes were removed by interactive pixel editing and median filtering.

A number of processing methods applicable to comets (Larson & Slaughter 1992) were used to enhance low-visibility details of the innermost coma. Azimuthal renormalisation processing was performed to reduce the average intensity profile around the photo-centre. Pixel intensities of the original image I are here transformed according to

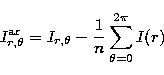$\begin{displaymath} I_{r,\theta}^{\rm ar} = I_{r,\theta} - \frac{1}{n}\sum_{\theta=0}^{2\pi} I(r)\end{displaymath}$

(2)

where n is the number of pixels within the annulus of radius r. The method was employed by rotating the source frame in steps of $\Delta\theta=10\hbox{$^\circ$}$ about the photo-centre location, successively adding rotated frames and normalising the generated image to unity photo-centre intensity. The rotationally normalised image was then subtracted from its source frame.

As the innermost coma was highly asymmetric around the photo-centre, defects were created by this method. This is also true throughout all of the imaged coma, including the prominent shell structure at greater radii, which generated a non-smoothly varying radial intensity profile. This introduced shells of negative intensity in the anti-solar direction at subtraction.

Rotational gradient processing was performed to enhance features due to the rotational component of motion of dust emission. The rotational gradient algorithm performs according to

$\begin{displaymath} I_{r,\theta}^{\rm rg} = I_{r,\theta} - I_{r,\theta+\Delta\theta}\end{displaymath}$

(3)

where $\Delta\theta$ is the amount of rotational shift. $\Delta\theta$ of $10\hbox{$^\circ$}$ and $20\hbox{$^\circ$}$ were used; at larger values excessive spurious information was introduced, rendering difficulties in interpretation. As the rotational gradient algorithm is a shift difference method, structure in the processed image displays intensity gradients, and thus differences of emission activity. Images may therefore be difficult to interpret in terms of physical opacity within the coma, especially in the case of such an active comet as Hale-Bopp.

Temporal derivative processing was employed to study possible short-term variations in the morphology of the coma. This technique enhances intensity differences between the two involved images due to dust motion, both azimuthal and radial, relative to the photo-centre. Resulting intensity is

$\begin{displaymath} I_{x, y}^{\rm td} = I_{t_1,x,y} - I_{t_2,x,y} \end{displaymath}$

(4)

where t₁ and t₂ are the times of subsequent images. As with the processing methods described above, it is a powerful method of locating moving features but requires great care in interpretation.

Unsharp masking (Gonzales & Woods 1992) processing was used to remove the general radial intensity function of the coma. It is a straightforward method directly depicting locations of features and at the same time removing the major part of the large-scale brightness variations, but not as powerful as the other three methods in the case of an indistinct object. By subtracting a smoothed copy of the original image, having a larger characteristic width and lower mean intensity of the central intensity peak of the source frame, large-scale intensity differences are effectively reduced. The method is applied according to

$\begin{displaymath} I_{x, y}^{\rm um} = \tens{F} \cdot I_{x,y}\end{displaymath}$

(5)

where matrix F,

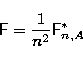$\begin{displaymath} \tens{F} = \frac{1}{n^2} \tens{F}^*_{n,A}\end{displaymath}$

(6)

is multiplied with each pixel of I. $A\ge1$ describes the weight w of the high-pass filter $\tens{F}^*$ , which is a matrix of size $n\times n$ where n is an uneven integer. All elements of $\tens{F}^*$ have numeric values of -1, except for the central element whose value is

3 Data reduction and processing