2 Reduction of the photographic plates

The process of the reduction of photographic plates starts with the determination of the cartesian coordinates X and Y. For the catalogs POSS, Schmidt 88, and Schmidt 94 the plates were first digitized with PDS microdensitometers. The plates of the series Schmidt 88 were digitized with the PDS microdensitometer of the Observatory of Munster, Germany, and the coordinates X and Y were determined using their computer software. The plates of the series Schmidt 94 were digitized with the PDS microdensitometer of the Department of Astronomy of the Yale University. The respective X and Y coordinates were derived from these scans by J. Lee of the Yale University using programs developed by himself. The original scans of this series were used to test an image adjustment method which was subsequently applied to the scans of the POSS plates. The POSS plates were digitized using the PDS microdensitometer of the Space Telescope Institute, and the data were made available to us. The plates of the series Schmidt 90 were measured with the Zeiss PSK2 stereo-comparator of CIDA. For the Paris and Oxford zones of the Astrographic Catalogue and for the plate series by Heckmann (1929) the original measurements were used.

Each of the Schmidt plate series presented different specific problems. Systematic errors caused by the plate bending mechanism of the Schmidt Camera were found in Schmidt 88 series (Abad 1995). A small movement of the mirror of the telescope mainly on the y-axis direction was present when the Schmidt 90 plates were taken. And finally, light came into the box containing the Schmidt 94 plates, before they were taken, producing a small degradation of the back ground over one side of each plate.

Such problems as well as the saturation of the brightest stars of the POSS plates, were used to check a new function which reproduce the real profile of the digitalized images better than the gaussian functions. The function created make use of the arctangent function (Abad 1996).

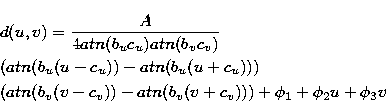$$\begin{eqnarray} &&\hspace*{-3mm} d(u,v) = \frac{A}{4atn(b_uc_u)atn(b_vc_v)} \no... ...-3mm}(atn(b_v(v-c_v))-atn(b_v(v+c_v)))+ \phi_1+\phi_2u+\phi_3v \end{eqnarray}$$ (1)

where,

$$u=(x-x_0)\cos(\phi)+(y-y_0)\sin(\phi) \\$$ (2)

$$v=-(x-x_0)\sin(\phi)+(y-y_0)\cos(\phi)$$ (3)

(x₀, y₀) center of the image,

$\phi$ angle between axis of symmetry of the image and axis of the digitalization,

A maximum density of the image,

b_u and b_v slope parameters,

c_u and c_v width parameters and,

$\phi_1$, $\phi_2$, $\phi_3$ coefficients representing the background.

A simple modification of the above equation would make it possible to adapt the artificially created profile to the asymmetric real profile. Varying b_u, b_v, c_u and c_v different symmetries can be produced in either axis, thus permitting adaptation to a large variety of image shapes. The above profile is particularly useful for images with a saturated center and hence a flat-topped profile. The latter is the case for at least most of the reference stars. In fact, for saturated images the above profile equation is superior to the gaussian approximation, while for faint images the latter gives more consistent results. The parameters of the function, above all the coordinates of the center, are determined by least squares in an iterative process. The profile parameters are strongly related to the image brightness, which is related to the total pixel count. Thus initial values for all parameters can readily be found once the mentioned relations are approximately known.

In this paper only images of the POSS plates were analyzed with the new function.

In order to get the equatorial coordinates a linear block adjustment method derived by Stock (1981) was used for each plate series. After this first step, the plate model explained and applied by Abad (1998) is used. It consists in obtaining the field deformation depending on the position on the plate and on the magnitude from the differences, star by star, between the individual plate position and their averaged final position or the reference catalogue position if the star is contained in the reference catalogue. The individual plate position and their averaged final position were calculated both from the linear block adjustment. From these differences a general plate distortion pattern is derived which is then applied to the measured coordinates. A new block adjustment is carried out with the corrected coordinates, and these are again analyzed for a systematic distortion pattern. This process can be repeated until no systematic pattern is evident. Tables 2 and 3 contain the final results, separated into magnitude intervals for everyone of the series of plates or catalogs.

 

Table 2: Final errors for the entire Paris Zone and part of the Oxford Zone of the AC and for the POSS plates covering the coma area

$$\tiny \begin{tabular} {\vert r\vert rrr\vert rrr\vert rrr\v... ...oalign{\smallskip} \hline \noalign{\smallskip} \end{tabular}$$

 

Table 3: Final errors for the three Schmidt CIDA plates series covering the coma area

$$\tiny \begin{tabular} {\vert r\vert rrr\vert rrr\vert rrr\v... ...oalign{\smallskip} \hline \noalign{\smallskip} \end{tabular}$$

The catalogs which give their data in equatorial coordinates (Yale, Carlsberg, AGK2, AGK3, and the POSS data which were reduced with the PPM catalog as reference system) were all reduced to the Hipparcos system applying a weighted sliding polynomial scheme described by Stock & Abad (1988). The process interpolates the differences between the Hipparcos positions and the positions given by the respective catalog for stars common to both, making use only of stars up to a given maximum distance from the star whose position is to be corrected.

In order to convert the equinox and orientation of the catalog data to coincide to Hipparcos system, expressions given by Fricke et al. (1988) are used. An inadequate precession constants will simply add to the systematic differences which have to be determined anyway. To the position of the Hipparcos catalog the respective proper motions were added to allow for the epoch differences between Hipparcos and the catalog.

Weights are assigned to the differences, based on the same distances in the sense that the weight reaches unity at the point to be interpolated, and zero at the maximum distance. Using this interpolation scheme at equidistant coordinate intervals the distortion pattern of the respective catalog can be found. Example are shown in Figs. 1 and 2. Systematic differences, at times surprisingly large, are found between the AGK2 and AGK3 catalogs and the Hipparcos catalog. In order to show that these differences are real we shall compare as an example the difference between the AGK3 and the FK5, using the B1950.0 version of the latter. The coordinates of the AKG3 are given in the same system. Thus only the epoch difference of around nine years has to be taken into account. Proper motions corrections were applied to the positions of the FK5. The resulting differences are shown as an arrow diagram in Fig. 3. It may be noted that the pattern in this figure is quite similar to that in Fig. 1 in the case of the AGK3.

  

Figure 1: Vector fields representing the positions differences between specific catalogues and the Hipparcos Catalogue. Light arrows represent individual differences. Each arrow has its origin on the point of coordinates $(\alpha,~\delta)$ of the respective common star. Modulus and direction are given by the composition of the two $\alpha$ and $\delta$ differences. Hipparcos system and epoch of the catalogue to study are used. The heavy arrows represent the systematic difference obtained after adjustment of a sliding polynomial to real differences (see text). The AGK2, the AGK3, and the Carlsberg catalogues are represented in a separating form

  

Figure 2: Vector fields representing the positions differences between specific catalogues and the Hipparcos Catalogue. Light arrows represent individual differences. Each arrow has its origin on the point of coordinates $(\alpha,~\delta)$ of the respective common star. Modulus and direction are given by the composition of the two $\alpha$ and $\delta$ differences. Hipparcos system and epoch of the catalogue to study are used. The heavy arrows represent the systematic difference obtained after adjustment of a sliding polynomial to real differences (see text). The Heckmann, the Yale and the POSS catalogues are represented in a separating form

  

Figure 3: Position differences between the AGK3 and the FK5 catalogs. For the FK5 positions the B1950.0 version was used, and corrected to the epoch of the AKG3 plates, using the proper motions of the FK5 catalog