3 Integrated colours for the reference population

To present and to discuss the results of theoretical simulations we will assume as a reference frame (RF) the results concerning a stellar population with solar composition (Y=0.27, Z=0.02) where a total number N=30000 of stars is distributed according to a Salpeter IMF ($\alpha=2.35$)between 0.6 and 25 $M_{\odot}$. After discussing theoretical predictions concerning such a sample, we will refer to this "archetype'' to investigate the influence of changing the assumptions either on the IMF or on the chemical composition.

  

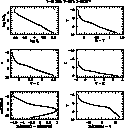Figure 2: Theoretical log($L/L_{\odot}$), log($T_{\rm e}$) RF model for an age of t = 10 Myr (upper left panel) compared with the corresponding predicted CMD for selected filters

  

Figure 3: As Fig. 2 but for t = 100 Myr

  

Figure 4: As Fig. 2 but for t = 800 Myr

  

Figure 5: As Fig. 2 but for t = 5 Gyr

To begin with, we present a selected sample (top-left panels of Figs. 2-5) of the theoretical log$L/L_{\odot}$ vs. log $T_{\rm eff}$ diagrams as obtained adopting (for graphic reasons) N = 3000 and for four representative ages ($10^7,\ 10^8, \ 8\ 10^8,\ 5\ 10^9$ years). Bearing in mind that the "stars'' plotted into theoretical diagrams represent the contributor to the total integrated flux of the population, the figure shows the well known occurrence for which young clusters are dominated by hot giants, whereas for larger ages the flux from Red Giant and Asymptotic Giant Branch stars begins dominating. Theoretical expectations about broad band colours can be better understood by looking at Fig. 2 to Fig. 5 where we compare, for each selected cluster age, the theoretical log$L/L_{\odot}$ vs. log $T_{\rm eff}$ diagrams with similar diagrams but for selected photometric bands.

One should in particular notice the curious CMD of stellar populations of different ages, as seen by HST red leaked filters (see also Chiosi et al. 1997). One finds that in the UV CMD (F152M vs. F152M - F307M) the MS discloses an unusual turn back at F152M - F307M $\simeq 0.9$ which means that, in such filter system, faint cool MS stars have a colour very similar to the stars populating the upper portion of the MS. Note also that cool core He-burning stars have rather "blue'' colours. Both these effects will strongly influence the expectations about cluster integrated light.

Bearing in mind such a scenario, we present in Fig. 6 (Tables 1a,b) theoretical expectation about cluster integrated colours as obtained from cluster populated by 30000 stars between 0.6 and 25 $M_{\odot}$.The labeled errors show the 1 $\sigma$ dispersion of the results obtained in 100 independent simulations. One can note that all the HST UV colours disclose monotonic relationships with the age, up to 10⁹ yr, thanks to the fact that most of the flux emitted at these wavelengths is generated by the more luminous main sequence stars.

  

Figure 6: Time evolution of integrated V magnitude and selected colours of the RF models (see text)

At $\log t \simeq 9$ the HST UV colours loose their sensitivity to variation in age and become roughly constant. This is not due to the variation in the UV flux of the population, but it is the result of the red leak of the HST filters which transmit the flux emitted by RGB stars and by the numerous low MS stars. This can be seen in Fig. 7, where the colour expected by HST filters is plotted against the colour obtained by theoretical filters centered at similar wavelengths and with a passband of 200 Å, but without red leak. The red leak, then, acts in the way of simulating the presence of "blue'' stars in the UV CMD. However, the hot stars of the MS termination are brighter than the "redleaked" cool stars up to $\log t \simeq 9$. For this reason the relation HST UV integrated colours vs. age shown in Fig. 2 holds up to this age and becomes almost flat for larger ages. In conclusion, the previous discussion indicates that the red leak plays a relevant role when interpreting HST UV integrated colours.

  

Figure 7: Correlation between HST-UV and Barbero et al. (1990) integrated colours. The arrows in the labels indicate the direction running from low to large ages. Note the red leak effect in HST-UV colours

Coming back to Fig. 6, one finds that all the broad band colours show a relatively flat minimum, i.e. a bluer colour, at intermediate ages. This is due to the occurrence in the younger population of red supergiants experiencing their He-burning phase. In particular, very young populations ($\simeq 10^7$ yr) are expected to have even redder V-K values than very old one ($\ge 10^9$) yr. This result will be further examined in discussing the effect of metallicity on present models. Another interesting feature of the broad band colours is the change of slope decreasing the age at $\log t \simeq 8.6$ due to the appearance of the Red Giant Branch which leads to redder colours.

Before closing this section, we notice that the total abundance of stars can play a significant role in determining the integrated colour of a stellar cluster. Poorly populated clusters should be affected by large statistical fluctuations in the distribution of luminous stars in the CM diagram, which in that case is no longer led by the evolutionary constraints, but governed by stochastic rules. We have already found that N = 30000 gives satisfactorily small fluctuations. However, to have more light on such an occurrence, we explored the behavior of the RF population at 10 Myr, 100 Myr and 1 Gyr and for different total numbers of stars (N = 100, 500, 1000, 3000, 7500, 10000, 30000, 45000) by computing a series of 100 models for each given age and N value. The top left panel in Fig. 8 shows, for each N value, the 1 $\sigma$ dispersion of the expected cluster integrated V magnitude as computed for the three selected cluster ages. The other panels in the same figure show theoretical expectations about cluster integrated colour given as a function of the integrated V magnitude of the cluster through the relation depicted by the top left panel. As expected, for each given V magnitude, one finds that decreasing the cluster age integrated colours appear more and more affected by statistical fluctuations, as a consequence of the stochastic contribution from few giants stars in a rapid evolutionary phase.

  

Figure 8: The integrated V magnitude as function of the total number of stars populating the RF model (top left panel) and a selected sample of integrated colours as a function of the cluster integrated V magnitude (see text). Each panel shows the result of simulation for three selected ages t = 10 Myr (solid line), t = 100 Myr (dotted line) and t = 1 Gyr (dashed line)

As an use result, one finds - e.g. - that for an age of 10 Myr the Johnson colours B-V, V-K (and V-I) do not correlate with cluster evolutionary status unless the cluster is brighter than about V = -9. This is not the case for UV HST colour, which are much less affected by the stochastic occurrence of red giant stars. As a whole, data in Fig. 8 give a useful warning on the use of integrated colour of stellar clusters. Bearing in mind these results, in the following we will limit our study to populations for which the MS is "dominated'' by the IMF law, discussing in all case the result obtained from cluster populated by 30000 stars between 0.6 and 25 $M_{\odot}$.