An illuminated model is defined by its effective temperature
![]() ,its surface acceleration of gravity g,
mixing length parameter
,its surface acceleration of gravity g,
mixing length parameter ![]() ,and chemical composition
(fixed at solar abundance in this work).
The external illumination is parametrized by
the direction of
illumination
,and chemical composition
(fixed at solar abundance in this work).
The external illumination is parametrized by
the direction of
illumination ![]() (the cosine of
(the cosine of ![]() , the
incidence angle with respect to the surface normal),
the effective temperature of the heating star
, the
incidence angle with respect to the surface normal),
the effective temperature of the heating star ![]() ,and its apparent radius
,and its apparent radius ![]() (the ratio between the radius of the
heating star and the distance from its centre to the point on
the surface of the reflecting star).
The geometry of illumination in a double star system is shown in
Fig.1.
We kept
(the ratio between the radius of the
heating star and the distance from its centre to the point on
the surface of the reflecting star).
The geometry of illumination in a double star system is shown in
Fig.1.
We kept ![]() fixed at 1.5 for the reflecting star
atmosphere.
fixed at 1.5 for the reflecting star
atmosphere.
We noticed that the effect caused by illumination on the limb-darkening
was rather weakly dependent on the ![]() of the model.
This can be seen in Fig.2, where we show that the effect of
changing the
of the model.
This can be seen in Fig.2, where we show that the effect of
changing the ![]() from 3.5 to 5.0 corresponds to only
from 3.5 to 5.0 corresponds to only ![]() 7% and
7% and
![]() 9% of the overall effect of illuminating an atmosphere of
9% of the overall effect of illuminating an atmosphere of
![]() K by
K by ![]() K and
10000K, respectively.
Therefore, we did calculations only for
K and
10000K, respectively.
Therefore, we did calculations only for ![]() , as for this value
we achieve a representative mean effect of illumination for the interval
, as for this value
we achieve a representative mean effect of illumination for the interval
![]() .We study illuminated atmospheres with line absorption
(line-blanketed or ODF) in
convective equilibrium. The ODF tables limit the temperature
range of this study to those corresponding to (ZAMS) stars with masses
ranging from
.We study illuminated atmospheres with line absorption
(line-blanketed or ODF) in
convective equilibrium. The ODF tables limit the temperature
range of this study to those corresponding to (ZAMS) stars with masses
ranging from ![]() to
to ![]() .
.
This same model has been used to study, in another paper and for the
first time in the literature, the effect of illumination on the gravity
brightening exponent ![]() , another important parameter for LC
synthesis. That work (Alencar et al. 1998) is a continuation of the
study of the
, another important parameter for LC
synthesis. That work (Alencar et al. 1998) is a continuation of the
study of the ![]() exponent using stellar atmospheres
(Alencar & Vaz 1997).
exponent using stellar atmospheres
(Alencar & Vaz 1997).
We calculated models with relative fluxes
(![]() )ranging from 0 to 2, whenever possible (
)ranging from 0 to 2, whenever possible (![]() ).
Those values are easily found in the literature
amongst many types of binary systems. Using
).
Those values are easily found in the literature
amongst many types of binary systems. Using ![]() we find
we find
![]() for
V
for
V![]() Pup (detached, Andersen et al. 1983), 0.338 for LZCen
(detached, Vaz et al. 1995), 0.386 for RYAqr (semi-detached,
Helt 1987), 0.660 for DH Cep (detached, Hilditch et al. 1996), 1.35
for AT Peg (algol, Maxtedetal.1994), 2.39 for HU Tau
(algol,
Maxted et al. 1995) and 2.72 for TV Cas (algol,
Khalesseh&Hill 1992).
Pup (detached, Andersen et al. 1983), 0.338 for LZCen
(detached, Vaz et al. 1995), 0.386 for RYAqr (semi-detached,
Helt 1987), 0.660 for DH Cep (detached, Hilditch et al. 1996), 1.35
for AT Peg (algol, Maxtedetal.1994), 2.39 for HU Tau
(algol,
Maxted et al. 1995) and 2.72 for TV Cas (algol,
Khalesseh&Hill 1992).
Many of the binary systems above also have temperatures
that fall in our selected ranges: RY Aqr (![]() K and
K and
![]() K), AT Peg (4898K and 8395K), HU Tau (5495K and 12022K)
and TV Cas (5248K and 10471K).
K), AT Peg (4898K and 8395K), HU Tau (5495K and 12022K)
and TV Cas (5248K and 10471K).
As with ![]() close
to
close
to ![]() we could not get large values of
we could not get large values of ![]() with
reasonable values of
with
reasonable values of ![]() , we studied models mostly ranging in the
interval
, we studied models mostly ranging in the
interval ![]() .The illuminating non-grey fluxes with
.The illuminating non-grey fluxes with ![]() K were
generated with the UMA code, while for higher
K were
generated with the UMA code, while for higher ![]() we took
the fluxes from Kurucz (1979).
We did calculate some models with
we took
the fluxes from Kurucz (1979).
We did calculate some models with ![]() close to
close to ![]() (
(![]() K, 4600K, 5500K, 6700K) and the results are
in agreement with our studies with higher
K, 4600K, 5500K, 6700K) and the results are
in agreement with our studies with higher ![]() so that our
results do apply for lower heating temperatures, also. However, we
advise caution in using those approximations extended to outside
the limits proposed in this work.
so that our
results do apply for lower heating temperatures, also. However, we
advise caution in using those approximations extended to outside
the limits proposed in this work.
In Sect.2.2 we give the results obtained with line-blanketed atmospheres illuminated by line-blanketed fluxes, showing differences in the calculations with the two distinct methods.
![\begin{figure}
\includegraphics [width=8.8cm]{ds8122f3.eps}\end{figure}](/articles/aas/full/1999/06/ds8122/Timg50.gif) |
Figure 3:
Adjusted limb-darkening laws for a non-illuminated model and
4 illuminated models (varying |
![\begin{figure}
\includegraphics [width=8.8cm]{ds8122f4.eps}\end{figure}](/articles/aas/full/1999/06/ds8122/Timg51.gif) |
Figure 4: The run of the temperature with the optical depth (Rosseland mean) for the models shown in Fig.3 |
![\begin{figure}
\parbox[]{0.1cm} {\epsfxsize=8.8cm \epsfbox{ds8122f5.eps} }\end{figure}](/articles/aas/full/1999/06/ds8122/Timg53.gif) |
Figure 5:
|
A first interesting result from Fig.3 is that, depending on the set of parameters chosen, we observe an effect of limb brightening instead of darkening. This can be understood as follows: when looking at a stellar disk we normally see the limb darker than the center because, despite of seeing the same optical depth in both, it corresponds to deeper, and consequently hotter, layers in the center than in the limb. In a illuminated star, the temperature distribution in the atmosphere becomes more and more homogeneous as we increase the illumination flux, until it reaches a state where there is no center-to-limb darkening and the star's brightness is the same throughout the stellar disk. This can be seen in Fig.4, where we show the temperature structure for the models shown in Fig.3. The larger the amount of infalling flux the higher the temperature of the external layers and the larger the region where it stays approximately constant.
If we keep increasing ![]() , by changing either
, by changing either
![]() ,
, ![]() or
or ![]() , we
reach a situation where the most external layers are hotter than the
internal ones. As we see more external layers looking at the limb than
looking at the center, we have a limb brightening effect.
In Fig.5 we illustrate that effect in three panels,
each with four
, we
reach a situation where the most external layers are hotter than the
internal ones. As we see more external layers looking at the limb than
looking at the center, we have a limb brightening effect.
In Fig.5 we illustrate that effect in three panels,
each with four ![]() vs.
vs. ![]() curves, varying the many
parameters.
The effect is, though, dependent not only on the amount of the
infalling flux. The first panel of Fig.5 shows
models that reach limb brightening with constant
curves, varying the many
parameters.
The effect is, though, dependent not only on the amount of the
infalling flux. The first panel of Fig.5 shows
models that reach limb brightening with constant ![]() and
incident direction, but changing
and
incident direction, but changing ![]() through changes
in
through changes
in ![]() . Panels 2 and 3 show that limb brightening can also be
achieved with constant
. Panels 2 and 3 show that limb brightening can also be
achieved with constant ![]() (= 0.5), either by keeping
(= 0.5), either by keeping ![]() constant and using different pairs of
constant and using different pairs of ![]() and
and ![]() , or by fixing
, or by fixing
![]() and changing
and changing ![]() and
and ![]() .We can also notice in Figs.3 and 5 that
the linear law (straight lines) is a poor approximation
for the limb-darkening of illuminated atmospheres, while for
.We can also notice in Figs.3 and 5 that
the linear law (straight lines) is a poor approximation
for the limb-darkening of illuminated atmospheres, while for
![]() K it fits well the non-illuminated
case (Fig.3). One should mention here that, although the models
of Fig.3 are similar to those calculated by CG, they do not report
any evidence for the limb brightening effect in their work.
K it fits well the non-illuminated
case (Fig.3). One should mention here that, although the models
of Fig.3 are similar to those calculated by CG, they do not report
any evidence for the limb brightening effect in their work.
The methods by CG and VH, used here to calculate the coefficients, differ
from each other in some important aspects. While CG emphasize
the point of using coefficients that best match the relation
![]() vs.
vs. ![]() , even if the total flux is not perfectly conserved,
VH says that the physical constraints of his method are introduced
in order to avoid non-physical coefficients. In non-illuminated
atmospheres CG find that the total emergent flux obtained by integrating
the intensities calculated from the adjusted coefficients (
, even if the total flux is not perfectly conserved,
VH says that the physical constraints of his method are introduced
in order to avoid non-physical coefficients. In non-illuminated
atmospheres CG find that the total emergent flux obtained by integrating
the intensities calculated from the adjusted coefficients (![]() ) does not differ
more than 2% from the total flux obtained from the model intensities
(
) does not differ
more than 2% from the total flux obtained from the model intensities
(![]() ),
and that when choosing a non-linear law, the difference vanishes.
We calculated the relation (
),
and that when choosing a non-linear law, the difference vanishes.
We calculated the relation (![]() )
for all our illuminated models, and the result for a
set of models is shown in Fig.6.
As noticed, the linear law is not a
good approximation when dealing with illuminated atmospheres.
We find that the mean difference between the fluxes is around 4% (with
a maximum of 26% in some models) in the case of a linear law and
less than 1% (however with a maximum of 6%) for the non-linear ones.
These results show that for an illuminated atmosphere the CG method
should be used with care, as, for some models, even choosing a non-linear
law, the flux is not conserved. Due to that we decided to adopt the
VH method in our calculations of all the results presented in Tables
1 and 2.
)
for all our illuminated models, and the result for a
set of models is shown in Fig.6.
As noticed, the linear law is not a
good approximation when dealing with illuminated atmospheres.
We find that the mean difference between the fluxes is around 4% (with
a maximum of 26% in some models) in the case of a linear law and
less than 1% (however with a maximum of 6%) for the non-linear ones.
These results show that for an illuminated atmosphere the CG method
should be used with care, as, for some models, even choosing a non-linear
law, the flux is not conserved. Due to that we decided to adopt the
VH method in our calculations of all the results presented in Tables
1 and 2.
Tables 1 and 2 are a sample of the tables with the monochromatic,
bolometric and passband-specific limb-darkening coefficients than can be
accessed electronically. We calculated coefficients for the linear,
quadratic, cubic, logarithmic and square root laws, for stars with
![]() heated by a
companion with
heated by a
companion with ![]() , with
relative fluxes ranging from 0.0 to 2.0 and the illumination direction,
, with
relative fluxes ranging from 0.0 to 2.0 and the illumination direction,
![]() ,
varying from 0.07 to 0.97. The parameter Q in Table 1 has the same meaning
as in VH. It is a quality factor that shows
how good is the fitting to the model intensities, the smaller the Q the
better the fitting:
,
varying from 0.07 to 0.97. The parameter Q in Table 1 has the same meaning
as in VH. It is a quality factor that shows
how good is the fitting to the model intensities, the smaller the Q the
better the fitting:
![\begin{displaymath}
Q_{\lambda}=\sqrt{\frac{\sum_{i=1}^{6}[R_{\lambda}(\mu_{i})-\widehat{R_{\lambda}}(\mu_{i})]^2}{6-m}}\end{displaymath}](/articles/aas/full/1999/06/ds8122/img63.gif) |
(5) |
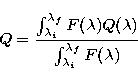 |
(6) |
|
|
|
|
![\begin{tabular}
{lcccccccc}
\hline\noalign{\smallskip}
band&\multicolumn{4}{c}{L...
...-3pt]
& & & & & & 0.17 & 0.15 & 0.15 \\ \hline\noalign{\smallskip}\end{tabular}](/articles/aas/full/1999/06/ds8122/img77.gif) |
When calculating with the CG method we do not determine the monochromatic
limb-darkening coefficients, so Q cannot be obtained by integrating
them.
In order to be able to compare the results from the CG and VH methods,
we used in Table 2, the following similar definition:
![\begin{displaymath}
Q_{\rm filter}=\sqrt{\frac{\sum_{i=1}^{6}[R_{\rm filter}(\mu_{i})-\widehat{R_{\rm filter}}(\mu_{i})]^2}{6-m}}\cdot\end{displaymath}](/articles/aas/full/1999/06/ds8122/img78.gif) |
(7) |
As already noticed by Claret & Giménez (1990), the limb-darkening
coefficients of an illuminated atmosphere strongly depend on many
parameters, making it difficult to find a simple function that
describes the effect. We propose, for the passband specific coefficients,
a solution to easily account for the effect in LC
synthesis programs, parametrizing with polynomials the results obtained.
In Eq.(8) K represents ![]() or
or ![]() of Eqs.(1) to (4) for the different limb-darkening laws:
of Eqs.(1) to (4) for the different limb-darkening laws:
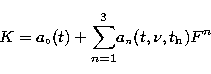 |
(8) |
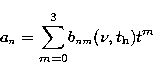 |
(9) |
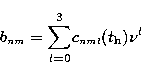 |
(10) |
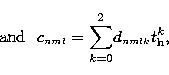 |
(11) |
In Table 3 we give a sample of the adjusted polynomial coefficients obtained from the data in Table 2 and in Fig.7 we show the adjusted polynomial surface for one chosen model. In the case of a non-linear law, we give in Table 3 the linear adjusted polynomial coefficients (cnm0_L, cnm1_L, cnm2_L, cnm3_L) followed by the non-linear ones (cnm0_NL, cnm1_NL, cnm2_NL, cnm3_NL). A complete version of Table 3 with the adjusted polynomial coefficients for the 9 chosen photometric filters (see Sect. 2.1) can be accessed in electronic form at the CDS.
This control in the case of illuminated atmospheres is more problematic. To the best of our knowledge only CG worked on the effect of external irradiation on the limb-darkening coefficients using numerical atmosphere models (UMA in that case), but their results are only presented in a qualitative way, making impossible a numerical comparison. We do not know of any other work on the effect of external illumination on the limb-darkening coefficients with models other than UMA.
However, if the theoretical approximations used are similar to those used in this work we expect that the results will be similar to ours, irrespective of the atmosphere model used in the study. And we are confident that the results derived here are better, even used as a first order approximation, than the use of constant limb-darkening coefficients overall in the analysis of eclipsing binary LC.
Copyright The European Southern Observatory (ESO)