3 Multiperiodicity and amplitude variability of 4 CVn

The pulsation frequency analyses were performed with a package of computer programs with single-frequency and multiple-frequency techniques (programs PERIOD, Breger 1990b; PERIOD98, Sperl 1998), which utilize Fourier as well as multiple-least-squares algorithms. The latter technique fits a number of simultaneous sinusoidal variations in the magnitude domain and does not rely on prewhitening. For the purposes of presentation, however, prewhitening is required if the low-amplitude modes are to be seen. Therefore, the various power spectra are presented as a series of panels in Fig. 4, each with additional frequencies removed relative to the panel above. The v and y data give identical results for the first 13 frequencies so that only the y results are presented in the left panel. For the additional frequencies, we present both the y and v (inverted) results in the right panel. Note that for the detected frequencies, the amplitude ratio, v/y, is near 1.5, as expected for these stars. This increases the confidence that the detected frequency peaks correspond to real pulsation modes, rather than noise artifacts.

  

Figure 4: Power spectrum of the 1997 photometry of 4 CVn. The different panels present the results after prewhitening a given number of previously detected frequencies. For the 13 main modes the y and v results are similar so that only y data are shown. For the additional modes, y and v (plotted inverted) data are presented separately at the lower right

One of the most important questions in the examination of multiperiodicity concerns the decision as to which of the detected peaks in the power spectrum can be regarded as variability intrinsic to the star. Due to the presence of nonrandom errors in photometric observations and because of observing gaps the predictions of standard statistical false-alarm tests give answers which are considered by us to be overly optimistic. In a previous paper (Breger et al. 1993) we have argued that a ratio of amplitude signal/noise = 4.0 provides a useful criterion for judging the reality of a peak for multisite data. This criterion can be somewhat relaxed for peaks at previously expected values; viz. harmonics or linear combination frequencies, where a value of 3.5 is adopted. In the present study the noise was calculated by averaging the amplitudes (oversampled by a factor of 20) over 5 cd^-1 regions centered around the frequency under consideration. For the two combination frequencies below 3 cd^-1, smaller intervals of 1 cd^-1 were chosen. The results are shown in Table 2, which also compares the new results to those found by re-analyzing the available data in the literature for the years from 1966 to 1984.

  

Table 2: Pulsation frequencies and amplitudes of 4 CVn

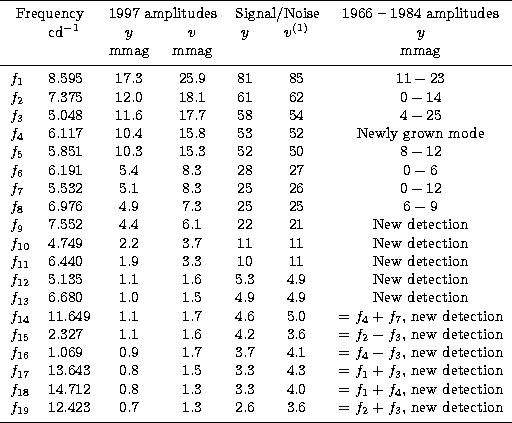⁽¹⁾ Amplitude signal/noise limit is 4.00 for newly discovered pulsation modes and 3.50 for "expected'' combination frequencies.

We noted earlier that the low-frequency terms found in APT data need to be considered with some caution. For 4 CVn, two low frequencies were detected. We regard their reality as quite probable since these peaks do not show up in the C1-C2 data and the values of the detected frequencies match the values calculated from frequency combinations exactly.

The average deviation of the observations from the fit are 3.0 mmag per single measurement in y and 4.0 mmag in v. This makes it possible to estimate the uncertainties of the amplitudes shown in Table 2. Based on the assumption that these residuals are random, we can apply the equation $\sigma$(a) = $\sigma$(m) (N/2)^-1/2, where a is the amplitude, $\sigma$(m) is the average residual of each data point, and N the number of measurements. We derive uncertainties of $\pm$0.09 and $\pm$0.12 mmag for the y and v amplitudes, respectively. Of course, in reality the sources of error are neither random nor independent of frequency (white noise). It is interesting to note that combining the two y, v data sets does not lower the noise level significantly and cannot improve the mode detection. Inspection of the data suggests two reasons: the computed noise in the frequency region under discussion is composed mainly of undetected additional modes and the measuring errors of y and v are not independent of each other. Although it is not possible to evaluate the errors in more detail, the present calculation can be useful to estimate whether or not observed amplitude variability is real.