 |
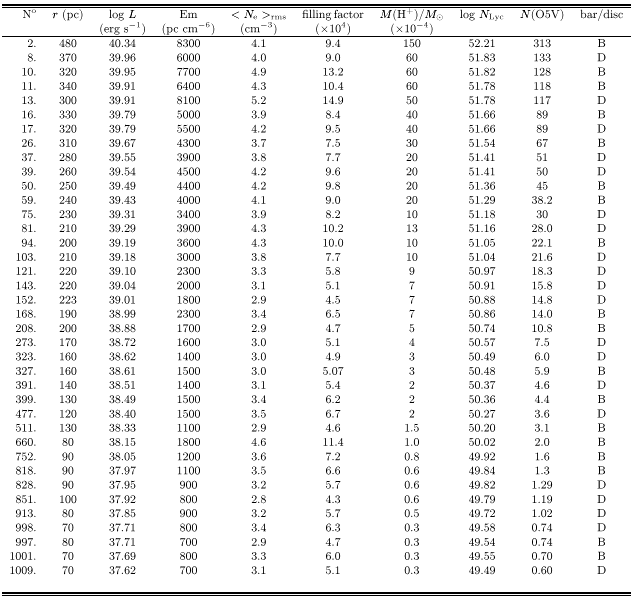
Using a distance to NGC 7479 of 31.92 Mpc (derived assuming H0=75 km s^-1 km s-1 Mpc-1) we employed the standard theoretical formula relating the surface brightness of an HII region with its emission measure Em (Spitzer 1978), assuming that the recombination lines are formed under the conditions of case B (Osterbrock 1974), to calculate Em for each HII region. A standard temperature of 104 K was taken for the calculation. We performed this for a total of 39 regions (22 in the disc and the rest in the bar), covering the full range of observed radii. They were chosen as isolated, so that the uncertainties in calculating their luminosities due to the overlapping of other regions are never as high as 10%. The results are plotted in Fig. 11. Values are given in Table 2 where the luminosity, radius, and emission measure are shown, as well as the electron density, computed from Em; the rms electron densities, derived from the emission measures, are plotted against radius of the HII region, in Fig. 12.
 |
In Fig. 13 we show the rms
electron densities ![]() for the same regions, plotted against luminosity.
The general ranges and behaviour of Em and
for the same regions, plotted against luminosity.
The general ranges and behaviour of Em and ![]() for NGC 7479 agree well with those
found by Kennicutt (1984) and by ourselves (Rozas et al. 1996b) for extragalactic
HII regions. Due to observational selection, these tend to be more
luminous and larger than Galactic regions.
for NGC 7479 agree well with those
found by Kennicutt (1984) and by ourselves (Rozas et al. 1996b) for extragalactic
HII regions. Due to observational selection, these tend to be more
luminous and larger than Galactic regions.
Kennicutt (1984) first showed that the
electron densities in the largest HII regions are of order 1 cm-3, which is
comparable with that of the general diffuse interstellar medium.
This is
not unexpected, as the powerful central sources can ionize
very large volumes of space, whose average matter density is not high. The
measured values of ![]() vary by a factor two for the whole set of regions
measured in NGC 7479; although the scatter within this range is high, there is
a clear trend for
vary by a factor two for the whole set of regions
measured in NGC 7479; although the scatter within this range is high, there is
a clear trend for ![]() to increase with L for high luminosities. This density increase is consistent
with the increase in surface brightness found for regions with L>1038.6
erg s-1, associated with the change of regime from ionization bounding to density
bounding hypothesised in Rozas et al. (1996b), in
Beckman et al. (1999), and in
Rozas et al. (1998).
to increase with L for high luminosities. This density increase is consistent
with the increase in surface brightness found for regions with L>1038.6
erg s-1, associated with the change of regime from ionization bounding to density
bounding hypothesised in Rozas et al. (1996b), in
Beckman et al. (1999), and in
Rozas et al. (1998).
To infer the uncertainties in the calculation of the Em and ![]() , we have estimated
the propagation of the error in the determination of the radius and in the flux of the
regions. Although most of the regions in the catalogue are not perfect spheres and,
in general, it is not easy to estimate the uncertainties in the determination of the radius, this is not
the case for the regions selected in the sample; they are nearly spherical since they have been
chosen for their circularity in projection. Errors in the determination of the radius are
, we have estimated
the propagation of the error in the determination of the radius and in the flux of the
regions. Although most of the regions in the catalogue are not perfect spheres and,
in general, it is not easy to estimate the uncertainties in the determination of the radius, this is not
the case for the regions selected in the sample; they are nearly spherical since they have been
chosen for their circularity in projection. Errors in the determination of the radius are ![]() 0.5 pix, and the uncertainty in the
determination of the flux is of the order of the flux in an external ring of the
region with width 0.5 pix and radius equal to that of the region.
0.5 pix, and the uncertainty in the
determination of the flux is of the order of the flux in an external ring of the
region with width 0.5 pix and radius equal to that of the region.
In this way, the relative uncertainty in the calculation of the Em is of the order of 50% for
smallest HII regions (log L < 38, below the completeness limit of the LF) and
![]() 10% in more luminous regions. For
10% in more luminous regions. For ![]() the resulting uncertainty is
between
the resulting uncertainty is
between
![]() for faint regions and decreases to well below 10% as the luminosity reaches
values typical of brighter regions.
In order to calculate the filling factor we need to know, as well
as the value of the rms electron density
for faint regions and decreases to well below 10% as the luminosity reaches
values typical of brighter regions.
In order to calculate the filling factor we need to know, as well
as the value of the rms electron density ![]() values of the in situ electron
density
values of the in situ electron
density ![]() for each region. We have not measured these values for NGC 7479,
but have used a "canonical'' mean value of 135 cm-3 obtained by
Zaritzky
et al. (1994) for 42 HII regions in a large sample of galaxies, via the intensity
ratio of the forbidden SII doublet
for each region. We have not measured these values for NGC 7479,
but have used a "canonical'' mean value of 135 cm-3 obtained by
Zaritzky
et al. (1994) for 42 HII regions in a large sample of galaxies, via the intensity
ratio of the forbidden SII doublet ![]() 6717, 6731 Å. The value of
6717, 6731 Å. The value of ![]() might
well differ from bar to disc and it would certainly be worth making direct
spectroscopic comparison in NGC 7479. However for the present we cannot improve on the use of a
constant value for all HII regions.
might
well differ from bar to disc and it would certainly be worth making direct
spectroscopic comparison in NGC 7479. However for the present we cannot improve on the use of a
constant value for all HII regions.
The implicit
model is that an HII region is internally clumpy, so that the observed flux
comes from a high density component, which occupies a fraction ![]() (filling factor) of the
total volume; the rest of the volume is filled with low density gas which
makes a negligible contribution to the observed emission line strengths. The
filling factors, computed from
(filling factor) of the
total volume; the rest of the volume is filled with low density gas which
makes a negligible contribution to the observed emission line strengths. The
filling factors, computed from ![]() for the regions range from
for the regions range from
![]() to
to ![]() , a range which coincides well with those found for 5
galaxies in Rozas et al. (1996b).
Values of
, a range which coincides well with those found for 5
galaxies in Rozas et al. (1996b).
Values of
![]() can also be used to estimate the mass of ionized
gas, by integrating over the measured volume of the region, and multiplying
by the mass of a hydrogen atom, using the formula:
can also be used to estimate the mass of ionized
gas, by integrating over the measured volume of the region, and multiplying
by the mass of a hydrogen atom, using the formula:
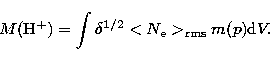 |
(2) |
Copyright The European Southern Observatory (ESO)