We have carried out a "Mini-survey'' with spectroscopic follow up on
the very low-mass star and brown dwarf candidates contained in
![]() 1% of the DENIS survey data. The "Mini-survey'' data are
representative of the survey quality, and its results can therefore be scaled
to evaluate the brown dwarf content of DENIS. The image data from the high
latitude part (
1% of the DENIS survey data. The "Mini-survey'' data are
representative of the survey quality, and its results can therefore be scaled
to evaluate the brown dwarf content of DENIS. The image data from the high
latitude part (![]()
![]() ) of 47 survey strips (for a total surface
area of 230 square degree), as produced
by the Paris DAC, were hand processed to create catalogs of I, J and
K
) of 47 survey strips (for a total surface
area of 230 square degree), as produced
by the Paris DAC, were hand processed to create catalogs of I, J and
K![]() photometry. From these we identified a sample of objects
for which infrared H- and K-band spectroscopy was carried out, in
order to "clean'' the dirty sample and evaluate its level of
contamination.
photometry. From these we identified a sample of objects
for which infrared H- and K-band spectroscopy was carried out, in
order to "clean'' the dirty sample and evaluate its level of
contamination.
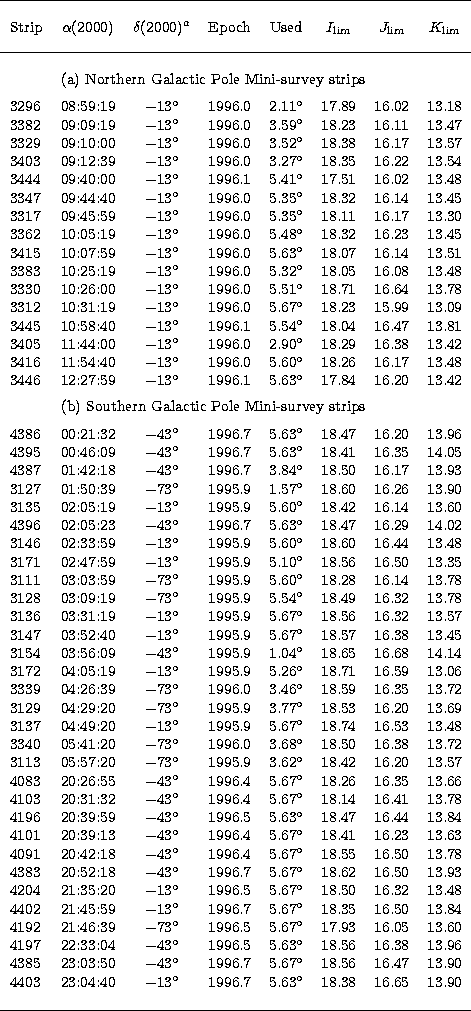
Notes: a - Strips centered on: -13 |
The 47 strips used for the Mini-survey (see Table 1) were chosen to maximise galactic latitude and to obtain useful right ascension coverage during our follow-up spectroscopic observing runs - the table is split into two sections as slightly different selection criteria were used for the northern and southern Galactic hemisphere samples. The image data were obtained from the Paris DAC and had been processed with version 4.2 of the standard pipeline software (Borsenberger 1997). The background levels are derived from a local clipped mean along the strip. Flat-field corrections are derived using observations of the dawn sky.
When this project was commenced the Leiden source extraction pipeline
was not yet operational. Source detection and photometry was therefore
performed in Grenoble, using the SExtractor package
(Bertin & Arnouts 1996). Sources were detected after smoothing the image with a 2![]() FWHP kernel, requesting a minimum of 5 contiguous pixels above a
threshold of 1.5 standard deviations of the original image for the
southern sample and 2.5 for the northern one. Adaptive aperture
photometry was then extracted from the original unsmoothed image. The
images of the closest photometric standards were identically
processed, and used to define the zero point of the instrumental
magnitudes. Since the objects of interest in our survey are close to our
limiting
magnitude, their photometric uncertainties are significant. As a result,
we have not attempted to apply the small corrections appropriate to
the airmass difference between our standard and strip observations, nor did
we correct for colour terms.
FWHP kernel, requesting a minimum of 5 contiguous pixels above a
threshold of 1.5 standard deviations of the original image for the
southern sample and 2.5 for the northern one. Adaptive aperture
photometry was then extracted from the original unsmoothed image. The
images of the closest photometric standards were identically
processed, and used to define the zero point of the instrumental
magnitudes. Since the objects of interest in our survey are close to our
limiting
magnitude, their photometric uncertainties are significant. As a result,
we have not attempted to apply the small corrections appropriate to
the airmass difference between our standard and strip observations, nor did
we correct for colour terms.
Completeness curves were estimated for each strip by fitting low order polynomials (n = 1-3) to the brighter part of the differential number count (i.e. Log(N)/Log(S)) curve for that strip, and using this fit to normalise the Log(N)/Log(S) curve. This normalised Log(N)/Log(S) curve was then used to evaluate the magnitude at which the strip is 50% incomplete. A typical example is shown in Fig. 1 and the resulting completeness limits for each strip are listed in Table 1. The variation in completeness level reflects changes in the sky level - due to the moon phase for I, and to ambient temperature variations for K.
 |
Figure 2:
I band finding charts for the objects listed in Table
2. The size of this chart is |
 |
Figure 3:
I band finding charts for the objects listed in Table
2. The size of this chart is |
 |
Figure 4:
I band finding charts for the objects listed in Table
2. The size of this chart is |
 |
Figure 5:
I band finding charts for the objects listed in able
2. The size of this chart is |
Even though VLMs and brown dwarfs are brightest at near-infrared
wavelengths, they are still vastly outnumbered in our flux
limited samples by intrinsically brighter and more distant stars. As an
illustration, the present mini-survey has obtained photometry at I
and
J for some ![]() stellar objects, of which less than 50 were finally
retained as VLM/BD candidates. With such a low selection fraction it
is essential that the selection scheme has a very low false alarm
rate, since even a small "blue leak'' of 0.01% would still produce a
sample dominated by G and K dwarfs.
stellar objects, of which less than 50 were finally
retained as VLM/BD candidates. With such a low selection fraction it
is essential that the selection scheme has a very low false alarm
rate, since even a small "blue leak'' of 0.01% would still produce a
sample dominated by G and K dwarfs.
Contamination by distant disk red giants increases at low galactic
latitudes, as does the general stellar background within which we have
to search for the brown dwarf signal. We initially imposed a galactic
latitude limit of ![]()
![]() - though this was later
relaxed to
- though this was later
relaxed to ![]()
![]() as our confidence in the processing
increased. All objects in 650
as our confidence in the processing
increased. All objects in 650![]()
![]()
![]() and
280
and
280![]()
![]()
![]() zones centered on the LMC (5
zones centered on the LMC (5![]() 23.6
23.6![]() - 69
- 69![]() 45
45![]() ) and the SMC (0
) and the SMC (0![]() 52.7
52.7![]() - 72
- 72![]() 50
50![]() ) were
also rejected, to avoid contamination by cool Magellanic Cloud
giants.
) were
also rejected, to avoid contamination by cool Magellanic Cloud
giants.
Objects detected within 20![]() of the edge of an image were ignored, as
were objects with clearly non stellar parameters. At the relatively
bright fluxes sampled by DENIS, galaxies are rare and typically much
bluer than late M dwarfs, and would therefore have been eliminated by
colour alone. Morphological rejection was primarily implemented to
exclude cosmic rays and some optical ghosts. Finally, all sources
within a
of the edge of an image were ignored, as
were objects with clearly non stellar parameters. At the relatively
bright fluxes sampled by DENIS, galaxies are rare and typically much
bluer than late M dwarfs, and would therefore have been eliminated by
colour alone. Morphological rejection was primarily implemented to
exclude cosmic rays and some optical ghosts. Finally, all sources
within a ![]() pixel zone 86pixels north of every bright
(J<10, K<8) source were ignored. Multiple reflections within the
DENIS dichroic splitters produce a faint infrared ghost, which has no
counterpart at I and can thus have extremely red apparent colours.
pixel zone 86pixels north of every bright
(J<10, K<8) source were ignored. Multiple reflections within the
DENIS dichroic splitters produce a faint infrared ghost, which has no
counterpart at I and can thus have extremely red apparent colours.
The three individual channels were then merged, using the I channel as a position reference. A linear transformation (offset, rotation,
and
scaling factor) between the other channels and this master channel was
determined by minimizing the sum of the squared distances between
all unsaturated stars brighter than I<17, J<15
and K<13.4. The J and
K object lists were then searched for matching objects within 3![]() of each I object to produce a three colour catalog for each strip.
Because source confusion is never a problem at the galactic latitudes
analysed here, this simple procedure was extremely effective.
of each I object to produce a three colour catalog for each strip.
Because source confusion is never a problem at the galactic latitudes
analysed here, this simple procedure was extremely effective.
Candidates were then selected in the three colour catalogs. To avoid
contamination by cosmic rays, sources were required to be detected in
at least two pass bands. For the objects of interest, J is always the
most sensitive passband, so two classes of objects were selected: (1)
objects with a very red I-J; and (2) objects with J and K detections
but no I detection. The latter criterion aimed to select extremely low
temperature objects (![]() K) with colours similar
to Gl229B - visual inspection of all these candidates revealed no
reliable detections beyond objects also selected on I-J. In the
remainder of this paper we consider only objects with very red I-J
colours. The northern sub-sample was processed first, and we
selected all objects with I-J> 2.75, or I-J> 2.2 for the brighter
ones. In view of the large number of selected objects with large
photometric errorbars (and presumably with an actual I-J bluer than 2.5),
we changed the selection criteria for the southern sample
and retained all objects with
K) with colours similar
to Gl229B - visual inspection of all these candidates revealed no
reliable detections beyond objects also selected on I-J. In the
remainder of this paper we consider only objects with very red I-J
colours. The northern sub-sample was processed first, and we
selected all objects with I-J> 2.75, or I-J> 2.2 for the brighter
ones. In view of the large number of selected objects with large
photometric errorbars (and presumably with an actual I-J bluer than 2.5),
we changed the selection criteria for the southern sample
and retained all objects with ![]() .
.
Inspection of the image data for these selected objects showed that
![]() 80% were contaminated by bad pixels or cosmic rays, and had
much bluer intrinsic colours.
This large artefact fraction illustrates a well known difficulty
when looking for needles in haystacks (the population of interest
represents less than 0.01% of the number of detected stars).
It suffices that a very small fraction of the 99.99% of higher mass
stars is affected by a bad pixel or a cosmic rays for it to
dominate the very low mass star and brown dwarfs region of the color-color
diagram.
Since such contamination could not be
selected against using the extracted source parameters, we visually
inspected the image data for all the initially selected VLM/BD
candidates. One reason for this relatively high level of sample
contamination is that version 4.2 of the Paris DAC software used
incorrect bad pixel flagging - future DENIS data will be
significantly improved in this respect. Cosmic rays will also be
identified with increased precision in future DENIS data by a neural
network classifier, to be used in the next generation of the Leiden
DAC extraction software (E. Bertin, private communication).
80% were contaminated by bad pixels or cosmic rays, and had
much bluer intrinsic colours.
This large artefact fraction illustrates a well known difficulty
when looking for needles in haystacks (the population of interest
represents less than 0.01% of the number of detected stars).
It suffices that a very small fraction of the 99.99% of higher mass
stars is affected by a bad pixel or a cosmic rays for it to
dominate the very low mass star and brown dwarfs region of the color-color
diagram.
Since such contamination could not be
selected against using the extracted source parameters, we visually
inspected the image data for all the initially selected VLM/BD
candidates. One reason for this relatively high level of sample
contamination is that version 4.2 of the Paris DAC software used
incorrect bad pixel flagging - future DENIS data will be
significantly improved in this respect. Cosmic rays will also be
identified with increased precision in future DENIS data by a neural
network classifier, to be used in the next generation of the Leiden
DAC extraction software (E. Bertin, private communication).
The objects remaining after this visual sample culling are listed
in Table 2. Table 2a shows the
list of objects identified for spectroscopic follow-up which
constitute a sample with I-J> 2.8.
Table 2b lists the remaining objects selected from
the DENIS data. The positions provided are based on the telescope
encoder readings, and are accurate to ![]()
![]() ,Much better position will be produced by the final DENIS pipeline.
,Much better position will be produced by the final DENIS pipeline.
| Figure 6: I-J/J-K colour-colour diagram for the objects selected from the DENIS strips and for templates from the literature. Open triangle: spectroscopically observed; filled triangle: not spectroscopically observed; solid circle: template M dwarfs from Leggett (1992) and Tinney, Mould & Reid (1993). All DENIS objects redder than our completeness limit of I-J=2.8 were spectroscopically observed |
Infrared spectroscopic observations were carried out on the 3.9 m
Anglo-Australian Telescope (AAT) on the nights of 1996 April 9 and 10
(UT) and 1996 October 21 and 22 (UT). On both runs the Infra-Red
Imaging Spectrograph (IRIS - Allen et al. 1993) was used in its
cross-dispersed HK echelle mode. This provides complete wavelength
coverage from ![]() m, at a resolution of
m, at a resolution of
![]() , and a dispersion of
, and a dispersion of
![]() . A slit of width 1.4
. A slit of width 1.4![]() and length
13
and length
13![]() was used.
was used.
Observations were typically of 20 minutes total integration time, and were
made with the object being nodded between two positions on the slit.
Reductions were performed using the Figaro data reduction package
(Shortridge 1993) and followed a standard procedure: the data were sky
subtracted using pairs of nodded observations, straightened to remove the
curvature of the echelle orders and the wavelength dependent "tilt'' of the
IRIS slit, and extracted using a modified version of the Figaro ANAL
routine to remove any residual sky spectrum left after pair-subtraction. A
variety of arcs (Ne, Ar, Cu, Hg and Xe) were used to construct a wavelength
calibration good to ![]() Å, which was applied to all the spectra.
Å, which was applied to all the spectra.
Spectra of late F-type and early G-type stars were used to create flux
calibrations. Because of the water vapour content at the AAT site, we did
not attempt to correct for absorption near the atmospheric H2O bands.
Standards were observed every few hours, at
airmasses within ![]() of the program object observations. The observed
standards had their H Brackett lines corrected by hand. The lines were
identified by dividing each standard by a G-type spectrum in which the H
lines are negligibly weak. The CO bands beyond 2.2
of the program object observations. The observed
standards had their H Brackett lines corrected by hand. The lines were
identified by dividing each standard by a G-type spectrum in which the H
lines are negligibly weak. The CO bands beyond 2.2 ![]() m were not
corrected, as these were weak (i.e. less than a few percent) in even the
latest G5 standards. Lastly, the photometry of
Carter & Meadows (1995)
was used to put these standards on an approximate flux scale. While
the relative fluxes obtained for our program stars are good to better than
5%, the absolute fluxes are no better than
m were not
corrected, as these were weak (i.e. less than a few percent) in even the
latest G5 standards. Lastly, the photometry of
Carter & Meadows (1995)
was used to put these standards on an approximate flux scale. While
the relative fluxes obtained for our program stars are good to better than
5%, the absolute fluxes are no better than ![]() .
.
 |
Figure 7:
IRIS HK echelle spectra for representative DENIS dwarfs
from Table 2. All spectra have been normalized by
their flux integrated between 2.09 and 2.11 |
 |
Figure 9:
IRIS HK echelle spectra of the template dwarf objects listed in
Table 3. All spectra have been normalized by their
flux integrated between 2.09 and 2.11 |
Notes: |
 |
Figure 10:
IRIS HK echelle spectra of the template giants
(cf. Table 3),
and the two DENIS objects classified as giants in Sect. 2.4.1. All
spectra have been normalized by their flux integrated between 2.09
and 2.11 |
Figures 7 and 8 present a sample of
the spectra obtained for the program objects listed in
Table 2. A sample of comparison objects was also observed -
in particular four late-type giants, and a large number of late-type
dwarfs. These are listed in Table 3 and shown in
Figs. 9 and 10. Because the AAT
is a relatively low-altitude site, it is not possible to make
observations through the atmospheric water vapour bands. These have
been marked on the figures. However, even outside these regions both
the dwarf and giant spectra show the broad stellar H2O
absorption bands characteristic of these low temperature
atmospheres. CO bandheads are seen from ![]() m in all the
spectra, though some of the giant spectra also show CO in the
m in all the
spectra, though some of the giant spectra also show CO in the
![]() m region. Numerous spectral lines due to neutral metals
are also seen - in particular, Na I
m region. Numerous spectral lines due to neutral metals
are also seen - in particular, Na I ![]() m and Ca I
m and Ca I
![]() m (Tinney et al. 1993). There is also a strong
absorption in many of the dwarfs at
m (Tinney et al. 1993). There is also a strong
absorption in many of the dwarfs at ![]() m, which
remains unidentified.
m, which
remains unidentified.
A comparison of the giants and dwarfs in Figs. 9
and 10 shows that for high signal-to-noise ratio
observations the presence of Na in absorption at 2.20 ![]() m indicates
that the atmosphere is at high (i.e. dwarf) gravities
(Jones et al. 1994;
Tinney et al. 1993). However, for much of our data, such a
criteria cannot be used because of the signal-to-noise available. A
giant dwarf discriminant which can be used at lower S/N is the
strength of CO bandhead at 2.29
m indicates
that the atmosphere is at high (i.e. dwarf) gravities
(Jones et al. 1994;
Tinney et al. 1993). However, for much of our data, such a
criteria cannot be used because of the signal-to-noise available. A
giant dwarf discriminant which can be used at lower S/N is the
strength of CO bandhead at 2.29 ![]() m. Following
Jones et al. (1993) we
therefore define a CO index as the ratio of the integrated flux in bands
at
m. Following
Jones et al. (1993) we
therefore define a CO index as the ratio of the integrated flux in bands
at ![]() m and
m and ![]() m.
m.
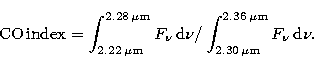 |
(1) |
The giant classification of DENIS-PJ1228-2510 is supported by its
position above the dwarf sequence in Fig. 6 and its bright
apparent magnitude (I=10.7, I-K=3.7). If we assume a dwarf status
for this star the colour-magnitude diagram of
Tinney (1996) would put
it at a distance of ![]() . Discovering such a nearby star in
the limited area covered by the present survey is unlikely.
Giant stars at these effective temperatures have
. Discovering such a nearby star in
the limited area covered by the present survey is unlikely.
Giant stars at these effective temperatures have ![]() (Lang 1991), or
(Lang 1991), or ![]() (Bessell et al. 1998). If we
interpret DENIS-PJ1228-2510 and J0944-1310 as being giants then, we
place them at distances of
(Bessell et al. 1998). If we
interpret DENIS-PJ1228-2510 and J0944-1310 as being giants then, we
place them at distances of ![]() kpc and
kpc and ![]() kpc
respectively. The latter is extreme for giant stars, but not unreasonably so.
Carbon stars, for example, are known at distances of up to
kpc
respectively. The latter is extreme for giant stars, but not unreasonably so.
Carbon stars, for example, are known at distances of up to ![]() kpc
(Totten & Irwin 1998). The giant status of J0944-1310 is, however, based on
one of our noisier infrared spectra and will require confirmation.
kpc
(Totten & Irwin 1998). The giant status of J0944-1310 is, however, based on
one of our noisier infrared spectra and will require confirmation.
DENIS-P J1228-2510 is bright enough that its DENIS colours are well determined, and they show that it lies 0.4 magnitudes above the dwarf sequence in the I-J/J-K diagram. Although the exact location of the giant sequence for the DENIS filter set has not yet been established, 0.4 magnitudes is the typical separation between the dwarf and giant sequences in these filters at this spectral type (Bessell & Brett 1988). With DENIS data alone, however, such a photometric criterion can only be used for stars which are at least two magnitudes brighter than the detection limit. In general follow-up photometry or spectroscopy is thus essential to separate giants from dwarfs.
Jones et al. (1994) have shown that luminosity (L) and/or effective
temperature (![]() ) information can be obtained for late-type
dwarfs using features in their infrared spectra. In particular, the
strength of H2O (as measured by the slope of the pseudo-continuum
in regions of stellar H2O absorption) is a sensitive measure of the
) information can be obtained for late-type
dwarfs using features in their infrared spectra. In particular, the
strength of H2O (as measured by the slope of the pseudo-continuum
in regions of stellar H2O absorption) is a sensitive measure of the
![]() of the stellar photosphere. For main sequence dwarfs,
therefore, a relationship between L and the strength of H2O
features can obviously be obtained, since there is essentially a
one-to-one mapping between L and
of the stellar photosphere. For main sequence dwarfs,
therefore, a relationship between L and the strength of H2O
features can obviously be obtained, since there is essentially a
one-to-one mapping between L and ![]() .
.
The same is also largely true for brown dwarfs. As they age
they slide along an extension of the main sequence in an H-R
diagram (see e.g. D'Antona & Mazzitelli 1985;
Burrows et al. 1989;
Burrows et al. 1997). The luminosity spread in this main
sequence "extension'' due to mass and age differences is ![]() 1
magnitude, which is similar to that seen due to metallicity variation
in low-mass stars (e.g. Tinney et al. 1995). So even in the absence
of parallaxes or atmospheric models, spectral features can provide
luminosity information for brown dwarfs, as they do for low-mass
stars.
1
magnitude, which is similar to that seen due to metallicity variation
in low-mass stars (e.g. Tinney et al. 1995). So even in the absence
of parallaxes or atmospheric models, spectral features can provide
luminosity information for brown dwarfs, as they do for low-mass
stars.
We therefore use the slope of a straight-line fit to each ![]() spectrum in the wavelength ranges
spectrum in the wavelength ranges ![]() m and
m and
![]() m to define two H2O indices. These wavelength
regions were chosen because they are dominated by H2O absorption,
and because they lie wholly within single echelle orders in our IRIS
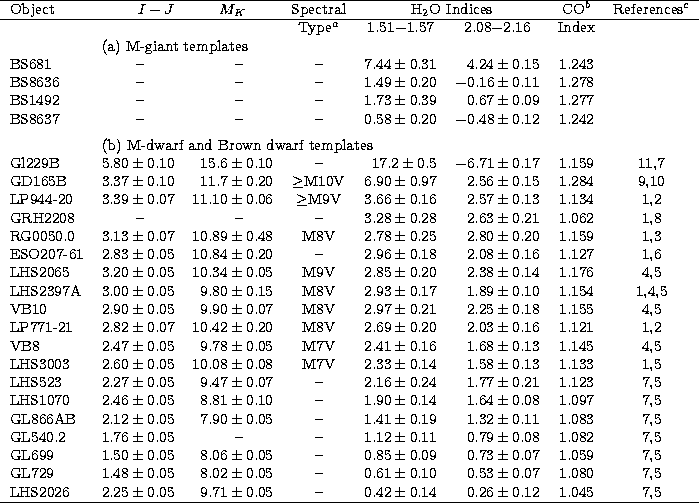
spectra. The indices are presented for each program object
in Table 2, and for each comparison object in Table
3. Also included in Table 3 are the
corresponding indices for the objects GD165B
(Jones et al. 1994) and
Gl229B (Geballe et al. 1996). The quoted uncertainties are those
produced by the least-squares fitting procedure. In the two cases
where repeated observations are available (DENIS-P J0205-1159 and
J1228-1547) the measured indices are consistent within
the derived uncertainties.
m to define two H2O indices. These wavelength
regions were chosen because they are dominated by H2O absorption,
and because they lie wholly within single echelle orders in our IRIS
spectra. The indices are presented for each program object
in Table 2, and for each comparison object in Table
3. Also included in Table 3 are the
corresponding indices for the objects GD165B
(Jones et al. 1994) and
Gl229B (Geballe et al. 1996). The quoted uncertainties are those
produced by the least-squares fitting procedure. In the two cases
where repeated observations are available (DENIS-P J0205-1159 and
J1228-1547) the measured indices are consistent within
the derived uncertainties.
Figures 11b and d show these indices plotted as a
function of I-J colour, while Figs. 11c and e show them
plotted as a function of MK. The H-band (![]() m)
H2O index can be seen to show a smooth dependence on L and/or
m)
H2O index can be seen to show a smooth dependence on L and/or
![]() . The K-band index (
. The K-band index (![]() m), on the other hand,
shows a marked turnover somewhere between effective temperatures
corresponding to GD165B (
m), on the other hand,
shows a marked turnover somewhere between effective temperatures
corresponding to GD165B (![]() K;
Kirkpatrick et al. 1998)
and those corresponding to the
low-temperature (
K;
Kirkpatrick et al. 1998)
and those corresponding to the
low-temperature (![]() K) brown dwarf Gl229B. This turnover is
almost certainly due to the onset of CH4 absorption in the K-band
for temperatures below 1500 K - this is clearly seen in Gl229B in
Fig. 9. The H2O indices for all observations of
the Mini-survey objects are also plotted in Figs. 11b
and
d as a function of their DENIS I-J colour. We can immediately see
that none of the DENIS objects show H2O indices indicating them to
be as cool as Gl229B. This is not surprising, since the CH4
features of Gl229B are distinctive, and would be immediately
apparent in the spectra. However, it is comforting to see that the
H2O indices confirm this expectation.
K) brown dwarf Gl229B. This turnover is
almost certainly due to the onset of CH4 absorption in the K-band
for temperatures below 1500 K - this is clearly seen in Gl229B in
Fig. 9. The H2O indices for all observations of
the Mini-survey objects are also plotted in Figs. 11b
and
d as a function of their DENIS I-J colour. We can immediately see
that none of the DENIS objects show H2O indices indicating them to
be as cool as Gl229B. This is not surprising, since the CH4
features of Gl229B are distinctive, and would be immediately
apparent in the spectra. However, it is comforting to see that the
H2O indices confirm this expectation.
In order to use these H2O indices to estimate absolute magnitudes
for the Mini-survey objects, we need to establish a
calibration. Figure 11 clearly shows that for objects as
faint, or fainter than, GD165B such a calibration is, at present,
poorly constrained. As the photometric distances for the coolest DENIS
objects are only ![]() pc, parallax measurement for these
objects will be straightforward. Further refinement of the
H2O-index-to-MK calibrations can therefore be expected in the
future. For the time
being, however, we adopt a minimal calibration
consisting of two linear fits to the available data, with a break at
MK=11. The adopted fits are shown in Figs. 11c and e.
As a result of the degeneracy in the
pc, parallax measurement for these
objects will be straightforward. Further refinement of the
H2O-index-to-MK calibrations can therefore be expected in the
future. For the time
being, however, we adopt a minimal calibration
consisting of two linear fits to the available data, with a break at
MK=11. The adopted fits are shown in Figs. 11c and e.
As a result of the degeneracy in the ![]() m H2O index it
is clearly not useful for estimating luminosities for our sample. We
have therefore derived MK estimates
(which are shown in Table
2) using the
m H2O index it
is clearly not useful for estimating luminosities for our sample. We
have therefore derived MK estimates
(which are shown in Table
2) using the ![]() m H2O index alone.
The uncertainties quoted in these estimated luminosities are based on
the measured uncertainties in the H2O indices propagated through
the H2O-index-to-MK calibration, added in quadrature to the
uncertainty in the calibration as derived from the residuals about
the
calibration fit. Objects with H2O indices outside the range
provided for by our calibration are denoted in the table as having
MK<8.
m H2O index alone.
The uncertainties quoted in these estimated luminosities are based on
the measured uncertainties in the H2O indices propagated through
the H2O-index-to-MK calibration, added in quadrature to the
uncertainty in the calibration as derived from the residuals about
the
calibration fit. Objects with H2O indices outside the range
provided for by our calibration are denoted in the table as having
MK<8.
Copyright The European Southern Observatory (ESO)