![\begin{displaymath}
W_2^{\rm cr.}= {1 \over 2} \int \bigl[ {\partial (U_{1}^{\rm...
...H}
\times {\partial (W_{1}) \over \partial h}\bigr] {\rm d}t \end{displaymath}](/articles/aas/full/1999/04/ds7187/img11.gif)
The second-order potential characterizing this effect is involving the Andoyer
variables h and H of the rotation of the Earth (Kinoshita 1977), and we can use
the same formulation as in Kinoshita & Souchay (1990) for the expression of the
second-order determining function involved, that is to say:
![\begin{displaymath}
W_2^{\rm cr.}= {1 \over 2} \int \bigl[ {\partial (U_{1}^{\rm...
...H}
\times {\partial (W_{1}) \over \partial h}\bigr] {\rm d}t \end{displaymath}](/articles/aas/full/1999/04/ds7187/img11.gif) |
(1) |
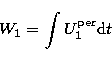 |
(2) |
![\begin{eqnarray}
&&\hspace*{-1em}U_{1}= {\kappa^{2} M_{\rm M} \over a_{\rm M}^{3...
...P_{2}^{2}(\sin \beta_{\rm S}) \cos 2(\lambda_{\rm S} - h)
\Bigr] \end{eqnarray}](/articles/aas/full/1999/04/ds7187/img14.gif) |
||
| (3) |
![]() and
and ![]() are respectively the masses of the Moon and the
Sun,(
are respectively the masses of the Moon and the
Sun,(![]() ,
, ![]() ,
, ![]() ) and (
) and (![]() ,
,![]() ,
, ![]() ) are
their respective set of spherical coordinates with respect to the mean ecliptic and the
mean equinox of the date. Notice that in a first approximation
) are
their respective set of spherical coordinates with respect to the mean ecliptic and the
mean equinox of the date. Notice that in a first approximation ![]() which represents
the latitude of the Sun with respect to the mean ecliptic of the date, can be set
to
which represents
the latitude of the Sun with respect to the mean ecliptic of the date, can be set
to ![]() , and that the terms of nutation due to the small displacements of
the Sun with respect to the mean ecliptic have been calculated by
Souchay &
Kinoshita (1996).
, and that the terms of nutation due to the small displacements of
the Sun with respect to the mean ecliptic have been calculated by
Souchay &
Kinoshita (1996).
![]() and
and ![]() are the basic constant values for the semi-major axes of the Moon
and of the Earth, considering the keplerian motion.
I is the obliquity angle (
are the basic constant values for the semi-major axes of the Moon
and of the Earth, considering the keplerian motion.
I is the obliquity angle (![]() ) associating
the two canonical
variables H and G, by the trivial equation (Kinoshita 1977):
) associating
the two canonical
variables H and G, by the trivial equation (Kinoshita 1977):
| (4) |
![\begin{displaymath}
{\partial [...] \over \partial H} = - {1 \over G \sin I}
{\partial [...] \over \partial I}\cdot \end{displaymath}](/articles/aas/full/1999/04/ds7187/img29.gif) |
(5) |
![\begin{displaymath}
W_{2}^{\rm cr.} = {1 \over 2} \int [{\bf A}] {\rm d}t \end{displaymath}](/articles/aas/full/1999/04/ds7187/img30.gif) |
(6) |
![\begin{displaymath}[{\bf A}]
= (\sin I \cos^{2}I) A_{1}
+ \left( {\sin^{2}I \co...
...\right) A_{5}+
\left({\sin^{2}I \cos I \over 4}\right) A_{6} \end{displaymath}](/articles/aas/full/1999/04/ds7187/img31.gif) |
(7) |
| (8.1) |
| (8.2) |
| (8.3) |
| (8.4) |
| (8.5) |
| (8.6) |
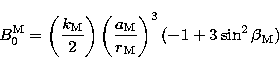 |
(9.1) |
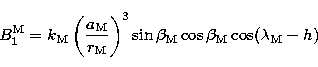 |
(9.2) |
 |
(9.3) |
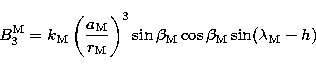 |
(9.4) |
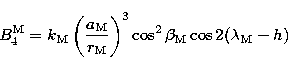 |
(9.5) |
 |
(9.6) |
 |
(9.7) |
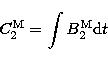 |
(9.8) |
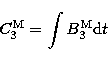 |
(9.9) |
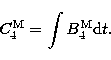 |
(9.10) |
 |
(10.1) |
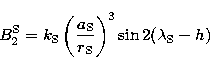 |
(10.2) |
 |
(10.3) |
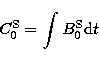 |
(10.4) |
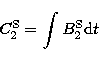 |
(10.5) |
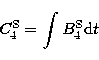 |
(10.6) |
 |
(11.1) |
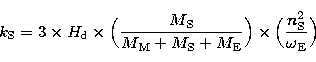 |
(11.2) |
![\begin{eqnarray}
&&\Delta \psi^{W2}_{\rm cr} = - \Delta h = - {\partial W_{2}^{\...
...\cos I \sin^{2}I \over 2 \sin I}\Bigr]
\times \int A_{6} {\rm d}t \end{eqnarray}](/articles/aas/full/1999/04/ds7187/img68.gif) |
||
| (12) |
![\begin{eqnarray}
&&\Delta \varepsilon^{W2}_{\rm cr} = - \Delta I =-\Bigl[ {1 \ov...
...- {\sin 2I \over 16}\Bigl[{\partial A_{6} \over \partial h}\Bigr].\end{eqnarray}](/articles/aas/full/1999/04/ds7187/img69.gif) |
||
| (13) |
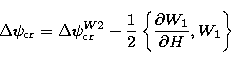 |
(14.1) |
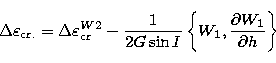 |
(14.2) |
![\begin{displaymath}
\Delta \psi_{\rm cr} = \Delta \psi^{W2}_{\rm cr} -{1 \over 2...
...i \times {\partial (\Delta \psi) \over \partial h}\Bigr) \Bigr]\end{displaymath}](/articles/aas/full/1999/04/ds7187/img74.gif) |
(15.1) |
![\begin{displaymath}
\Delta \varepsilon_{\rm cr} = \Delta \varepsilon^{W2}_{\rm c...
...\partial h} \Bigr)-
\cot \varepsilon (\Delta \varepsilon)^{2}]\end{displaymath}](/articles/aas/full/1999/04/ds7187/img75.gif) |
(15.2) |
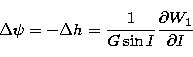 |
(16.1) |
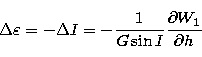 |
(16.2) |
For the computations relative to the present effect, we catch all the coefficients
up to a relative 10-8 with respect to the largest term, in the expressions ![]() ,
,![]() ,
, ![]() and
and ![]() which are used in Eqs. (8.1) to (8.6)
and (9.1) to (9.10). In a similar way, we take all the coefficients of nutation in
which are used in Eqs. (8.1) to (8.6)
and (9.1) to (9.10). In a similar way, we take all the coefficients of nutation in
![]() and
and ![]() larger than 0.1
larger than 0.1 ![]() as for the combinations
inside (15.1) and (15.2), which is quite enough if we want to reach the
as for the combinations
inside (15.1) and (15.2), which is quite enough if we want to reach the ![]() level for the resulting coefficients. These computations are made with the
Broucke
(1980) subroutines for manipulation of Fourier series, which are the same we used previously
for the reconstruction of the theory of nutation for a rigid Earth model
(Kinoshita & Souchay 1990).
level for the resulting coefficients. These computations are made with the
Broucke
(1980) subroutines for manipulation of Fourier series, which are the same we used previously
for the reconstruction of the theory of nutation for a rigid Earth model
(Kinoshita & Souchay 1990).
The results are listed in Table 1. This table constitutes a big improvement with respect to previous computations carried out manually (Zhu & Groten 1989; Kinoshita & Souchay 1990) by picking up only the largest coefficients in the potential. It seems that it is much more difficult to select these terms with a theory of nutation based on the classical equation for the angular momentum (Bretagnon et al. 1997; Roosbeek & Dehant 1997), because there is no clear method to separate them from the spin-orbit effect described in the next chapter.
We can remark also that no less than 68 coefficients
are present above the ![]() level, which demonstrates its rather big influence.
The number of coefficients is still 24 for
level, which demonstrates its rather big influence.
The number of coefficients is still 24 for ![]() , and 20 for
, and 20 for ![]() up to
up to ![]() .The by far largest component with argument
.The by far largest component with argument ![]() and amplitude
1.2206
and amplitude
1.2206 ![]() as results
naturally from the interactions between the nutations of the leading component at the
first order with argument
as results
naturally from the interactions between the nutations of the leading component at the
first order with argument ![]() . It was already calculated for the first time by
Kinoshita & Souchay (1990). As it was not taken into account before, this
explained the big 9.3 y signature when comparing the previous analytical
nutation (Kinoshita 1977) with numerical integration (Schastok et al. 1989),
which disappeared after the reconstruction of the theory, as was shown by
Souchay & Kinoshita (1991).
Notice also the 2 coefficients with amplitude
. It was already calculated for the first time by
Kinoshita & Souchay (1990). As it was not taken into account before, this
explained the big 9.3 y signature when comparing the previous analytical
nutation (Kinoshita 1977) with numerical integration (Schastok et al. 1989),
which disappeared after the reconstruction of the theory, as was shown by
Souchay & Kinoshita (1991).
Notice also the 2 coefficients with amplitude ![]() and
and ![]() in longitude (respectively
in longitude (respectively ![]() and
and ![]() in obliquity) around the
semi-annual period, and the 2 coefficients with
amplitude
in obliquity) around the
semi-annual period, and the 2 coefficients with
amplitude ![]() and
and ![]() in longitude (respectively
in longitude (respectively ![]() and
and ![]() in obliquity) around the fortnightly period.
At last we can also remark the clustering
of coefficients around these two fundamental periods.
in obliquity) around the fortnightly period.
At last we can also remark the clustering
of coefficients around these two fundamental periods.
Copyright The European Southern Observatory (ESO)