4 Performance

4.1 Sensitivity

The total efficiency of the Echelle spectrometer was estimated before the flight by measuring the efficiencies of the individual optical components. The product of these values resulted in a maximum effective area of 2.4cm².

For postflight recalibration we used a HST calibration spectrum of G191B2B. By comparing the fluxes within complete orders we estimated an effective area value for the central wavelength of each Echelle order. Values for Echelle orders that were contaminated by strong absorption lines (e.g. Ly-$\alpha$) were deleted from the data set. This procedure leads to a maximum effective area of 1.3cm² near 110nm (Fig. 4), which is based on all detector counts above the lower electronic threshold.

  

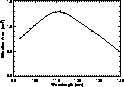Figure 4: Effective area curve for the Echelle spectrometer. The symbols denote the center wavelengths of those Echelle orders for which a fit value to the HST model spectrum was estimated

The 20$^{\prime\prime}$diameter of the diaphragm should be sufficient to maintain the total flux of the object, as the jitter of the ASTRO-SPAS was about $\pm$2$^{\prime\prime}$. But we have indications that the telescope was not precisely focused during some periods of the mission, due to thermal problems during unexpected flight modes of the ASTRO-SPAS. Together with the fact that some objects were not fully centered this led to significant nonstatistical variations of the count rates, which resulted in a reduction of the flux and thus sensitivity. Therefore the flux calibration was calculated for the maximum observed count rate for the corresponding target (also from other observations of this target, if necessary). This count rate was scaled with the registered count rate in the integrated image.

4.2 Spectral resolution

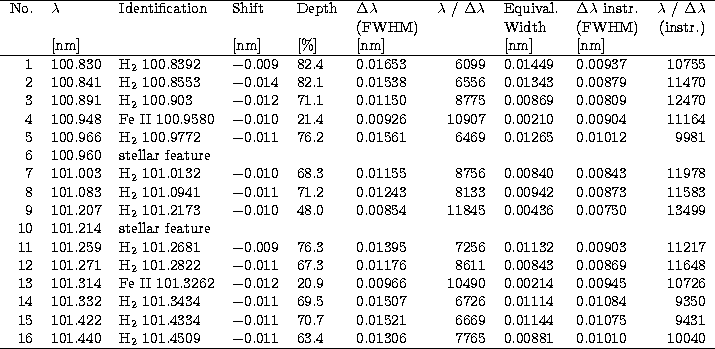
The spectrum of HD93521 with a signal to noise ratio of 20 to 30 is best suited to study the spectral resolution of the Echelle spectrograph. It shows many interstellar absorption lines, mainly from molecular hydrogen, which are very sharp and rather strong. Among a total of 814 interstellar line positions used for wavelength calibration, 159 line positions originated from this object. We coadded two observations of this object with integration times of 1080s and 660s respectively, taken within two successive orbits (Fig. 5).

  

Figure 5: Echelle image of HD93521. The numbers at the left side denote the Echelle orders. The image is shown in the electronic format with 1024$\times$512 pixels, which does not correspond to the square format of the detector of 40mm$\times$40mm. The Echelle spectrometer could show some more Echelle orders than the visible orders 40 to 61, but below the Lyman limit at 91.15nm all light is generally absorbed by interstellar hydrogen, so that none of the spectra contains any useful flux below this limit. (Orientation: long wavelengths are at top and at left side)

We fitted many of these absorption lines in the wavelength range from 96nm to 110nm with Gaussian profiles and calculated the ratio of wavelength to the FWHM of these lines. We got values mainly between $\lambda$/$\Delta$$\lambda$=7000 to 10000 with depths of 60% to 80% (Fig. 6 and Table1).

 

Table 1: Fitted Gaussian absorption profiles from the spectrum shown in Fig. 6. From the estimated equivalent widths a Gaussian instrument profile was calculated under the assumption that the original absorption line had an depth of 100%. The broad stellar features are fitted for a better reproduction of the continuum, as the fitting algorithm used supports only a linear continuum

We further estimated an upper limit for the width of the instrument profile: Assuming that the absorption lines had originally depths of 100% with the same equivalent width, we calculated the width of the instrument profile that would be necessary to reproduce the observed absorption line profiles. For simplicity we assumed Gaussian profiles for both the absorption lines and the instrumental profile and a quadratic addition of the widths. The resulting values for the FWHM of the instrumental profiles are in the range $\lambda$/$\Delta$$\lambda$=9000 to 13000 (Table1). As these calculations are estimates of a lower limit of the resolution of the Echelle spectrometer, we conclude that the achieved resolution of the Echelle spectrometer was significantly better than the goal of $\lambda$/$\Delta$$\lambda$=10000.

Another approach to estimate the achieved instrumental resolution is shown in Fig. 7. The equivalent widths of the fitted absorption lines are plotted against their observed $\lambda$/$\Delta$$\lambda$ values. A linear least square fit is applied to all data points (point No.9 was excluded from the fit in a conservative approach). Extrapolating this fitted straight line to an equivalent width of 0 should reproduce the instrumental resolution. The result is a value between $\lambda$/$\Delta$$\lambda$=11000 and 12000.

  

Figure 6: Part of the Echelle spectrum of HD93521. This demonstrates the resolution achieved with the Echelle spectrometer. The spectrum is plotted without any smoothing. The smooth curve plotted over the spectrum is a fit with several Gaussian shaped absorption profiles. The straight line shows the continuum used by the fitting algorithm. The continuum is corrected by additional broad absorption profiles (6 and 10). See Table 1 for the parameters of the fitted curves

  

Figure 7: Equivalent widths of fitted lines plotted against their observed $\lambda$/$\Delta$$\lambda$values (Table1). The straight line is a least square fit to the data points, except for absorption line No. 9, which was excluded in a conservative approach. Extrapolating the linear fit to an equivalent width of 0 the observed line width should reproduce the instrumental width. The values shown indicate an instrumental resolution between 11000 and 12000

This result is not really surprising, as the spectral resolution of 10000 was calculated for a fully illuminated 10$^{\prime\prime}$ diaphragm. Though the Echelle spectrometer was operated with a 20$^{\prime\prime}$ diaphragm the ASTRO-SPAS pointing jitter was $\pm$2$^{\prime\prime}$and therefore the effective object image size was much smaller than the assumed 10$^{\prime\prime}$.

Figure 8 shows the complete Echelle spectrum of HD93521 smoothed with a 11 pixel wide boxcar. The individual Echelle orders are plotted separately, the spectral range for each order is indicated at the top of the figure. The overlap region between adjacent orders increases with the order number. A small gap exists between orders 40 and 41 and between orders 41 and 42.

  

Figure 8: ORFEUSII Echelle spectrum of HD93521. The individual Echelle orders are plotted separately, the wavelength range for each order is indicated at the top of the figure. Except for orders 40/41 and 41/42 there is an overlap region between adjacent orders which increases with the order number. The spectrum is plotted with an 11 pixel wide boxcar smoothing