We first compute the probability of detecting the transit of a planetary
satellite in front of the parent star. We start by computing the luminosity
drop ![]() produced by an object, planet or satellite of a planet,
on the line of sight to a star of luminosity
produced by an object, planet or satellite of a planet,
on the line of sight to a star of luminosity ![]() . This can be expressed as
. This can be expressed as
![]() , where r0 is the radius of the object, and I
is the surface brightness of the star where the object is producing the
occultation. We assume that the star is spherical and that the radial
dependence of the surface brightness can be described by the standard
limb-darkening law
, where r0 is the radius of the object, and I
is the surface brightness of the star where the object is producing the
occultation. We assume that the star is spherical and that the radial
dependence of the surface brightness can be described by the standard
limb-darkening law ![]() . Here,
r is the projected distance from the star center to the object,
. Here,
r is the projected distance from the star center to the object, ![]() is
the radius of the star, and
is
the radius of the star, and ![]() is the limb-darkening parameter that depends
on wavelength. For reference, in the visible a solar-type star has
is the limb-darkening parameter that depends
on wavelength. For reference, in the visible a solar-type star has ![]() (Allen 1973, p. 171). Since
(Allen 1973, p. 171). Since ![]() is the integral of I(r) over
the star's area, we can write the relative drop in luminosity imprinted by
the object as:
is the integral of I(r) over
the star's area, we can write the relative drop in luminosity imprinted by
the object as:
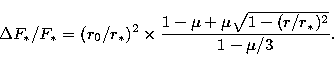 |
(1) |
Numerical evaluations of Eq. (1) show that the drop in luminosity caused
by an occulting object depends only weakly on the projected distance of
the object to the star center, except when the object is very close to the
limb. For example, adopting ![]() ,
Eq. (1) indicates that
,
Eq. (1) indicates that ![]() is only 30% smaller for
is only 30% smaller for ![]() than for r=0. In the
following, therefore, when computing detection probabilities for planets and
satellites of planets transiting in front of a parent star, we consider all
projected trajectories with
than for r=0. In the
following, therefore, when computing detection probabilities for planets and
satellites of planets transiting in front of a parent star, we consider all
projected trajectories with ![]() . As Eq. (1) shows,
. As Eq. (1) shows, ![]() is roughly of the order of
is roughly of the order of ![]() , and for a
Jupiter-like or Earth-like planet occulting a solar-type star this implies
, and for a
Jupiter-like or Earth-like planet occulting a solar-type star this implies
![]() or 10-4, respectively, at
or 10-4, respectively, at
![]() . For reference, COROT is expected to detect planets or satellites
with
. For reference, COROT is expected to detect planets or satellites
with ![]() , where
, where ![]() is the Earth radius.
is the Earth radius.
We do not speculate here
on the origin of satellites with radii ![]() that could be
detected with COROT. Their formation could be associated to that of
giant planets, or they could form or be capured ulteriorly. We note,
however, that the lifetimes of such satellites before they collapse on
their parent planets are expected to be relatively long because of the high
tidal dissipation factor of Jupiter-like planets (
that could be
detected with COROT. Their formation could be associated to that of
giant planets, or they could form or be capured ulteriorly. We note,
however, that the lifetimes of such satellites before they collapse on
their parent planets are expected to be relatively long because of the high
tidal dissipation factor of Jupiter-like planets (![]() ; see, e.g.,
Burns 1986). In fact, based on the calculations by Burns, the expected
lifetime of a satellite with
; see, e.g.,
Burns 1986). In fact, based on the calculations by Burns, the expected
lifetime of a satellite with ![]() at a distance
at a distance
![]() from a Jupiter-like planet with orbital period
from a Jupiter-like planet with orbital period ![]() days is
days is
![]() (where
(where ![]() is
the Jupiter radius). As mentioned in
Sect. 1, the
expected occurence of Jupiter-like planets is independent
of orbital radius.
It is conceivable, therefore, that extended
satellites be found around
Jupiter-like planets in relatively
close orbit (i.e., with short periods)
around solar-type stars.
is
the Jupiter radius). As mentioned in
Sect. 1, the
expected occurence of Jupiter-like planets is independent
of orbital radius.
It is conceivable, therefore, that extended
satellites be found around
Jupiter-like planets in relatively
close orbit (i.e., with short periods)
around solar-type stars.
Stellar variability, unless it is much stronger than that exhibited by
the Sun, should not prevent the detection of transits of even Earth-like
planets. In fact, the Sun variability is ![]() on a time scale of
several hours, as measured by the Solar Maximum Mission satellite, the Upper
Atmosphere Research Satellite, and the Solar and Heliospheric Observatory
for the Sun (Fröhlich 1987;
Willson & Hudson 1991). The photometric
variability due to sunspot activity may be more important, but it should
not be confused with planetary transits because it depends on wavelength
and is not periodic.
on a time scale of
several hours, as measured by the Solar Maximum Mission satellite, the Upper
Atmosphere Research Satellite, and the Solar and Heliospheric Observatory
for the Sun (Fröhlich 1987;
Willson & Hudson 1991). The photometric
variability due to sunspot activity may be more important, but it should
not be confused with planetary transits because it depends on wavelength
and is not periodic.
We now compute the probability for the transit of a planetary satellite to
be detected. In this section the satellite is assumed to be extended enough
to produce a detectable minimum in the lightcurve.
The detection probability is given by the product of two
independent probabilities, which we define as "geometric probability''
and "orbital probability''.
In the remainder of this paper, we express all distances in units of
![]() and all masses in units of a solar mass.
and all masses in units of a solar mass.
The geometric probability is the probability for the planet-satellite system to have a favorable orbital inclination angle so that the projected satellite orbit can intersect the star. We first describe the geometric conditions required for the transit of a planet and then extend the results to the case in which the planet has a satellite. We assume throughout this paper that the orbits are keplerian and circular. A transit of a planet is geometrically possible when the projected orbit intersects the star. The projected position of the planet with respect to the star center can be most generally parameterized as:
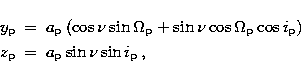 |
(2) | |
| (3) |
The geometric probability for a transit of the planet can be estimated by
noticing that it corresponds to all line-of-sight inclinations of the
planetary orbital plane less than the critical angle ![]() , where again
, where again ![]() is expressed in units of the stellar radius.
Therefore, the total geometric probability of a planetary transit is given
by the ratio of the area of detectability,
is expressed in units of the stellar radius.
Therefore, the total geometric probability of a planetary transit is given
by the ratio of the area of detectability, ![]() , to the entire
possible area covered by planetary orbits,
, to the entire
possible area covered by planetary orbits, ![]() . This is
. This is ![]() ,or
,or ![]() . The differential geometric probability that a planet transit
occurs with orbital inclination angle between
. The differential geometric probability that a planet transit
occurs with orbital inclination angle between ![]() and
and ![]() can then
be written as:
can then
be written as:
 |
(4) | |
| (5) |
| (6) |
We can reexpress ![]() in terms of the planetary orbital radius,
in terms of the planetary orbital radius, ![]() . The
satellite orbital radius must satisfy the condition
. The
satellite orbital radius must satisfy the condition ![]() ,
where
,
where ![]() and
and ![]() are the planet Roche and Hill radii, respectively.
We parameterize
are the planet Roche and Hill radii, respectively.
We parameterize ![]() in terms of the Hill radius as
in terms of the Hill radius as ![]() , where
, where ![]() is the mass of the planet in units of a
solar mass, with
is the mass of the planet in units of a
solar mass, with ![]() . We further adopt the notation
. We further adopt the notation
![]() . With these notations, the maximum line-of-sight
inclination of the planetary orbital plane leading to a transit of the
satellite,
. With these notations, the maximum line-of-sight
inclination of the planetary orbital plane leading to a transit of the
satellite, ![]() , can be rewritten in terms of
, can be rewritten in terms of ![]() , X and
, X and ![]() .The differential geometric probability that a satellite transit occurs when
the planetary orbital inclination angle ranges between
.The differential geometric probability that a satellite transit occurs when
the planetary orbital inclination angle ranges between ![]() and
and ![]() is thus:
is thus:
 |
(7) | |
| (8) |
| (9) |
In the remainder of this paper, all expressions are computed by adopting
the above parameterization of ![]() in terms of
in terms of ![]() via the parameter
via the parameter
![]() , that allows us to sample all possible satellite orbital radii. The
results can be reformulated straightforwardly in the context of any
alternative parameterization using
, that allows us to sample all possible satellite orbital radii. The
results can be reformulated straightforwardly in the context of any
alternative parameterization using ![]() .
.
For a satellite transit to occur, the satellite must be in the part
of its orbit intersecting the star when the planet is in a favorable
location. This can be described by an orbital probability function.
We assume that the duration of the observations is at least as long as
the planetary orbital period. Therefore, the planet will always sample the
part of its orbit that is favorable for a satellite transit if the condition
![]() is satisfied. To express the orbital probability function
of the satellite, it is convenient to introduce the variable
is satisfied. To express the orbital probability function
of the satellite, it is convenient to introduce the variable
| (10) |
Three limiting conditions characterize the orbital probability associated to
a geometrically possible transit (![]() ). First, the planet itself
is transiting, and at a given time the satellite's orbit projects entirely
on the stellar area. This corresponds to
). First, the planet itself
is transiting, and at a given time the satellite's orbit projects entirely
on the stellar area. This corresponds to ![]() , and in this
case the orbital probability is unity. Second, at any given time the
satellite's orbit projects only partially on the star area. In this case the
orbital probability depends on the comparison between
, and in this
case the orbital probability is unity. Second, at any given time the
satellite's orbit projects only partially on the star area. In this case the
orbital probability depends on the comparison between ![]() and the
stellar diameter. If
and the
stellar diameter. If ![]() , the orbital probability, i.e., the fraction
of the satellite's orbit which will intersect the star as the planet orbits is
, the orbital probability, i.e., the fraction
of the satellite's orbit which will intersect the star as the planet orbits is
![]() . If, on the other hand,
. If, on the other hand, ![]() , then the
orbital probability reduces to
, then the
orbital probability reduces to ![]() .
.
The above limiting conditions on ![]() translate via Eq. (10)
into conditions on the line-of-sight inclination of the planetary orbital
plane,
translate via Eq. (10)
into conditions on the line-of-sight inclination of the planetary orbital
plane, ![]() , for given
, for given ![]() , X and
, X and ![]() . The orbital probability of
a geometrically possible satellite transit is therefore given as a function
of
. The orbital probability of
a geometrically possible satellite transit is therefore given as a function
of ![]() by:
by:
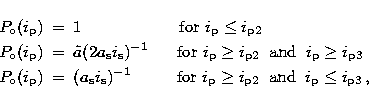 |
(11) | |
| (12) | ||
| (13) |
![\begin{eqnarray}
i_{\rm p2} & = & (1-Xa_{\rm p}i_{\rm ps})\left[a_{\rm p}(1+X)\r...
... & (X a_{\rm p} i_{\rm ps} -1)\left[a_{\rm p} (1-X)\right]^{-1}\,.\end{eqnarray}](/articles/aas/full/1999/03/ds7637/img74.gif) |
(14) | |
| (15) |
The detection probability of the satellite is the product of the geometric
and orbital probabilities. We let the planetary orbital radius ![]() vary and
fix the the angle between the planet and satellite orbital planes,
vary and
fix the the angle between the planet and satellite orbital planes, ![]() ,and the parameter X. Using the same notations as above,
the probability to detect a satellite transit is therefore
,and the parameter X. Using the same notations as above,
the probability to detect a satellite transit is therefore
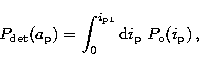 |
(16) |
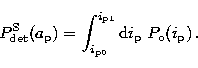 |
(17) |
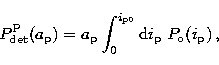 |
(18) |
As noted in Sect. 2.2, the form of the integrand in Eqs. (16)-(18) depends
on the value of ![]() relative to
relative to ![]() and i3. For fixed
and i3. For fixed ![]() and X,
this depends on the parameter
and X,
this depends on the parameter ![]() . More specifically, if
. More specifically, if ![]() and
and ![]() , then
, then ![]() ,
,
![]() and
and ![]() can be computed by breaking the
integrals in Eqs. (16)-(18) according to the rule
can be computed by breaking the
integrals in Eqs. (16)-(18) according to the rule
 |
(19) | |
| (20) | ||
| (21) |
Copyright The European Southern Observatory (ESO)