We use Johnson B-band CCD images of a group of spiral galaxies obtained at
the prime focus of the 2.5 m Isaac Newton Telescope, at the Observatorio del
Roque de los Muchachos, La Palma. The images were reduced using standard
routines, with a seeing-limited angular resolution close to 1 arcsec. The
observations and data reduction are described in detail in
Paper II. In
their original form (before deprojection) the orientation is north-right,
east-top. In this paper all images are deprojected. The positive
![]() -axes corresponds to the PAs listed in Table 2.
-axes corresponds to the PAs listed in Table 2.
A complete and detailed description of this method can be found in Puerari & Dottori (1992). We give a brief review here of the procedure, and of the notation and formulae used.
We consider the decomposition of a given distribution of intensities of a set
of continuous two-dimensional coplanar points into a superposition of
m-armed logarithmic spirals. Each point, associated with a pixel of the
image, with polar coordinates (![]() ) in the galaxian plane, is
weighted by the intensity of the corresponding pixel. An m-armed
logarithmic spiral is expressed by
) in the galaxian plane, is
weighted by the intensity of the corresponding pixel. An m-armed
logarithmic spiral is expressed by ![]() , where m is
the number of arms, i.e. the angular periodicity number, and p is related
to the pitch angle i of the spiral via the relation
, where m is
the number of arms, i.e. the angular periodicity number, and p is related
to the pitch angle i of the spiral via the relation ![]()
![]() . The
distribution of the points that follow the former conditions can be written
in terms of
. The
distribution of the points that follow the former conditions can be written
in terms of ![]() -functions, and its Fourier transform is then expressed
by
-functions, and its Fourier transform is then expressed
by
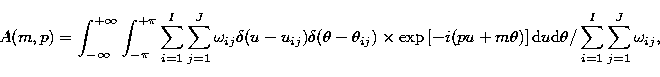 |
(1) |
![\begin{eqnarray}
A(m,p)\!=\!\left(\!\sum_{i=1}^{I}\! \sum_{j=1}^{J} \omega_{ij}\...
... \right] \right)\!/ \sum_{i=1}^{I} \!\sum_{j=1}^{J}\! \omega_{ij}.\end{eqnarray}](/articles/aas/full/1999/02/ds7722/img11.gif) |
(2) |
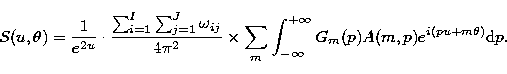 |
(3) |
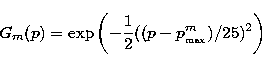 |
(4) |
The righthand side of Eq. (3) can be separated by variables in the form:
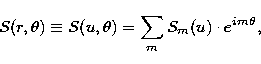 |
(5) |
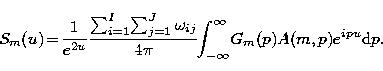 |
(6) |
The relative importance of the different spiral modes can be estimated from
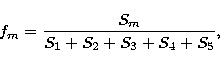 |
(7) |
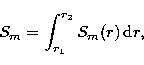 |
This method has been developed and applied by EEM and consists in decomposing a given image into images of different degrees of symmetry through rotations and subtractions, thereby obtaining the bi-, tri- and four-symmetric images S2, S3 and S4, respectively, together with the asymmetric image A2. This method maintains the non-linear spiral arm form, without introducing spurious inter-arm components. The authors also claim that this technique shows the m=1,2,3,4,... sub-components simultaneously over the whole image, which prevents confusion with field stars or star formation zones.
According to EEM, not only do galaxies apparently showing a high degree of symmetry, such as NGC 157 and NGC 4321 in this sample, have an important tri-symmetric component that is not evident in the images, but even galaxies with lower symmetry, such as NGC 6764 and NGC 7723, also possess this tri-symmetry. The 3-S structure extends from the 3:1 ILR to the 3:1 OLR, and, correspondingly, the 4-S structure from the 4:1 ILR to the 4:1 OLR.
Copyright The European Southern Observatory (ESO)