

Up: Imaging spectroscopy of planetary
PCA is a technique generally used to enhance the information content of
multiband data and to reduce the dimensionality of the data set (Davis
1986; Chevrel et al. 1994; Erard et al.
1991; Jaumann 1991). PCA uses a linear transformation
of the data to translate and rotate them in a new coordinate system that
maximizes the variance. The rows of the transformation matrix A are
composed of the eigenvectors of the covariance matrix Kx between the
bands. The matrix A performs a diagonalization of the covariance
matrix Kx such that the covariance matrix of the transformed imagery
| 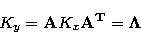 |
(1) |
is a diagonal matrix whose elements are the eigenvalues of Kx arranged
in descending value. The principal components decomposition therefore
results in a set of decorrelated data planes and the information is
contained in few PC images (the eigenvectors) while most of the noise is
segregated in the others components. The first transformed image is
approximately an albedo picture and depicts the average brightness of the
surface while the others components contain the color information. These
higher order components are used for our purposes. We applied this
technique to an image cube of the Moon composed of 128 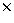 258 spectra
of 96 bands each, obtained by means of a visible-near infrared imaging
spectrometer (
258 spectra
of 96 bands each, obtained by means of a visible-near infrared imaging
spectrometer (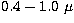 m spectral range,
m spectral range, 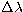 = 7.5 nm).
Details about the instrumentation can be found in Bellucci et al.
1998.
= 7.5 nm).
Details about the instrumentation can be found in Bellucci et al.
1998.
Table 1:
Statistics of three principal components of the image cube
discussed in the text. The units are in digital numbers
|
|
The PC transformation has not been directly applied to the raw image cube but to
a relative image cube. Each spectrum of the original data set, has been
normalized respect to an average spectrum of a small area (10 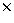 10
pixels) chosen within the image. This operation removes at the same time the
instrumental and atmospheric transfer functions and allows to enhance
spectral differences proper of the lunar surface only. Table 1 summarizes
the relevant statistics of 3 PC images which contain most of the image cube variance. Eigenvalues for bands that contain some information are larger than those that contain only noise. The corresponding PC images are spatially coherent, while the noise images do not contain any spatial information.
10
pixels) chosen within the image. This operation removes at the same time the
instrumental and atmospheric transfer functions and allows to enhance
spectral differences proper of the lunar surface only. Table 1 summarizes
the relevant statistics of 3 PC images which contain most of the image cube variance. Eigenvalues for bands that contain some information are larger than those that contain only noise. The corresponding PC images are spatially coherent, while the noise images do not contain any spatial information.
![\begin{figure}
\includegraphics [width=8.8cm,clip=]{fig2.eps}
\end{figure}](/articles/aas/full/1999/01/ds1504/Timg8.gif) |
Figure 2:
Raw image of the study region at 0.7 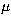 m. Main geologic
features are indicated m. Main geologic
features are indicated |
![\begin{figure}
\includegraphics [width=8.8cm,clip=]{fig3.eps}
\end{figure}](/articles/aas/full/1999/01/ds1504/Timg9.gif) |
Figure 3:
Principal components of the image cube discussed in the text |
Figure 2 shows a raw image at 0.7 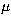 m of the Mare
Serenitatis/Tranquillitatis, Montes Haemus and Plinius region on the Moon.
The scale is 1.2 arcsec per pixel, while the seeing is about 2.5 arcsec.
The small crater in the center of Serenitatis is Bessel and will be used in
the following to evaluate the enhancement process.
Figure 3 shows the PC images. The PC1 image (Fig. 3a) is
the albedo picture. In the PC2 image (Fig. 3b) the Menelaus rim
and some features inside the crater are visible; also the Al-Bakri rim
and floor are well discernible. In general, the PC2 image shows more
details than raw image. The PC3 image (Fig. 3c) still contains
enough information to allow recognition of narrow features as the Menelaus
and Plinius rims and the Al-Bakri crater. Very narrow features, like
small craters, crater rims and ejecta, are also well visible. In order to
enhance the spatial contrast of the raw image shown in Fig. 2 by
utilizing the results of the PCA, we have applied on the raw image
m of the Mare
Serenitatis/Tranquillitatis, Montes Haemus and Plinius region on the Moon.
The scale is 1.2 arcsec per pixel, while the seeing is about 2.5 arcsec.
The small crater in the center of Serenitatis is Bessel and will be used in
the following to evaluate the enhancement process.
Figure 3 shows the PC images. The PC1 image (Fig. 3a) is
the albedo picture. In the PC2 image (Fig. 3b) the Menelaus rim
and some features inside the crater are visible; also the Al-Bakri rim
and floor are well discernible. In general, the PC2 image shows more
details than raw image. The PC3 image (Fig. 3c) still contains
enough information to allow recognition of narrow features as the Menelaus
and Plinius rims and the Al-Bakri crater. Very narrow features, like
small craters, crater rims and ejecta, are also well visible. In order to
enhance the spatial contrast of the raw image shown in Fig. 2 by
utilizing the results of the PCA, we have applied on the raw image 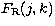 the following transformation:
the following transformation:
| ![\begin{eqnarray}
F_{\rm En}(j, k) &=& {\rm stretch}[F_{\rm R}(j, k)]\nonumber \\ && - {\rm stretch}[PC_{n}(j,
k) \times L(m, n)]\end{eqnarray}](/articles/aas/full/1999/01/ds1504/img11.gif) |
|
| (2) |
where  is the enhanced image, PCn(j, k) is one of the
three principal component images, L(m, n) is a Laplacian convolution
array. The j and k indices are the spatial coordinates of a pixel within
the image, while m=3 and n=3 are the dimensions of the convolution array
L. The Laplacian filter is:
is the enhanced image, PCn(j, k) is one of the
three principal component images, L(m, n) is a Laplacian convolution
array. The j and k indices are the spatial coordinates of a pixel within
the image, while m=3 and n=3 are the dimensions of the convolution array
L. The Laplacian filter is:
| ![\begin{displaymath}
L(3, 3) = \left [ \begin{array}
{rrr}
0 & -1 & 0 \\ -1 & 4 & -1 \\ 0 & -1 & 0
\end{array} \right ].\end{displaymath}](/articles/aas/full/1999/01/ds1504/img13.gif) |
(3) |
It is a second derivative edge enhancement filter that operates without
regard to edge direction (Ross 1995). In order to display the
result when both positive and negative pixel values rise, a stretch
operation is applied to each of the right-hand terms of Eq. (2). In this
way, brighter and darker values produced by the Laplacian can be seen. The
stretch[I] is a linear scaling operation:
| ![\begin{displaymath}
{\rm stretch}[I]= \frac{I-{\rm min}(I)}{{\rm max}(I)-{\rm min}(I)} \times
255.\end{displaymath}](/articles/aas/full/1999/01/ds1504/img14.gif) |
(4) |
Figure 4 shows schematically the sharpening procedure.
![\begin{figure}
\includegraphics [width=8.8cm,clip=]{fig4.eps}
\end{figure}](/articles/aas/full/1999/01/ds1504/Timg15.gif) |
Figure 4:
Block scheme of the sharpening method described in the text |


Up: Imaging spectroscopy of planetary
Copyright The European Southern Observatory (ESO)
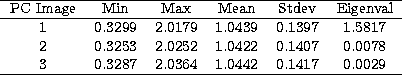
![]() m of the Mare
Serenitatis/Tranquillitatis, Montes Haemus and Plinius region on the Moon.
The scale is 1.2 arcsec per pixel, while the seeing is about 2.5 arcsec.
The small crater in the center of Serenitatis is Bessel and will be used in
the following to evaluate the enhancement process.
Figure 3 shows the PC images. The PC1 image (Fig. 3a) is
the albedo picture. In the PC2 image (Fig. 3b) the Menelaus rim
and some features inside the crater are visible; also the Al-Bakri rim
and floor are well discernible. In general, the PC2 image shows more
details than raw image. The PC3 image (Fig. 3c) still contains
enough information to allow recognition of narrow features as the Menelaus
and Plinius rims and the Al-Bakri crater. Very narrow features, like
small craters, crater rims and ejecta, are also well visible. In order to
enhance the spatial contrast of the raw image shown in Fig. 2 by
utilizing the results of the PCA, we have applied on the raw image
m of the Mare
Serenitatis/Tranquillitatis, Montes Haemus and Plinius region on the Moon.
The scale is 1.2 arcsec per pixel, while the seeing is about 2.5 arcsec.
The small crater in the center of Serenitatis is Bessel and will be used in
the following to evaluate the enhancement process.
Figure 3 shows the PC images. The PC1 image (Fig. 3a) is
the albedo picture. In the PC2 image (Fig. 3b) the Menelaus rim
and some features inside the crater are visible; also the Al-Bakri rim
and floor are well discernible. In general, the PC2 image shows more
details than raw image. The PC3 image (Fig. 3c) still contains
enough information to allow recognition of narrow features as the Menelaus
and Plinius rims and the Al-Bakri crater. Very narrow features, like
small craters, crater rims and ejecta, are also well visible. In order to
enhance the spatial contrast of the raw image shown in Fig. 2 by
utilizing the results of the PCA, we have applied on the raw image ![]() the following transformation:
the following transformation:
![\begin{eqnarray}
F_{\rm En}(j, k) &=& {\rm stretch}[F_{\rm R}(j, k)]\nonumber \\ && - {\rm stretch}[PC_{n}(j,
k) \times L(m, n)]\end{eqnarray}](/articles/aas/full/1999/01/ds1504/img11.gif)
![\begin{displaymath}
L(3, 3) = \left [ \begin{array}
{rrr}
0 & -1 & 0 \\ -1 & 4 & -1 \\ 0 & -1 & 0
\end{array} \right ].\end{displaymath}](/articles/aas/full/1999/01/ds1504/img13.gif)
![\begin{displaymath}
{\rm stretch}[I]= \frac{I-{\rm min}(I)}{{\rm max}(I)-{\rm min}(I)} \times
255.\end{displaymath}](/articles/aas/full/1999/01/ds1504/img14.gif)