4 Discussion

 

4.1 What is a core?

An important question to start with is how to define a core? In Papers I and II we assumed implicitly that a core is a region of noticeable CS emission towards our HMSF pointers (masers). Many of these regions have an apparent substructure; others might reveal it when observed with a higher resolution. Indeed, observations of higher CS transitions (with better angular resolution) by Lapinov et al. (1998) have revealed complex structure of several cores which show almost spherically symmetric appearance in CS J=2-1. It might be possible to consider the clumps constituting this substructure as individual cores. However, the internal fragmentation continues probably to smaller and smaller scales and it is not clear where it stops.

Taking this into account we prefer to consider these CS emitting regions as single entities having probably rather complex internal structure. Most of them are concentrated to well defined single emission peaks which coincide with powerful IR sources, masers, etc. Then, the fact that practically all these regions seem to be gravitationally bound (see below) also supports this approach.

4.2 Physical parameters of the cores

In Paper II we constructed statistical distributions of the core parameters on the basis of the SEST data. There was a hint of the decrease of the mean core density with the galactocentric radius. The new results presented here enable us to improve these statistics and to investigate further the galactic gradients of these parameters.

First we have to derive the physical parameters of the cores. For the sources of category I we make it in essentially the same way as in Papers I and II as described briefly in Sect. 2.4. The results are presented in Table 4.

  

Table 4: Physical parameters of the sources of category I

In addition, we give the IR luminosities of associated point IRAS sources and their colour temperatures ($T_{\rm d}$) from the ratio of the 60 and 100 $\mu$m fluxes calculated as in Henning et al. (1990).

For the sources of category II we are unable to derive LTE masses and densities in the same way. However, sizes and virial masses can be determined as for the category I sources. Our previous results (Papers I and II) as well as an inspection of the results for the category I sources show that LTE masses derived from the column densities and virial masses are very close to each other in most cases. So for the sources of category II we estimate the densities from the virial masses. The results of these estimations are presented in Table 5.

  

Table 5: Physical parameters of the sources of category II

The physical parameters determined for the sources of category III are given in Table 6.

  

Table 6: Physical parameters of the sources of category III

4.3 Statistical distributions of the parameters

As in Paper II when constructing statistical distributions of the core parameters we limit ourselves to the objects located within a certain distance from the sun in order to diminish the selection effects. We consider here two subsamples: (1) $1~\mbox{kpc} < d < 4$ kpc and (2) d < 5 kpc. The comparison of these subsamples shows the influence of the nearest and most distant sources. We combine here our previous SEST and present Onsala data. In total there are 37 cores in the first subsample and 43 in the second one with reliably determined parameters (categories I and II for the Onsala sample).

In addition to the CO brightness temperature, size, mean density, LTE mass and CS line width as in Paper II we consider here the IR luminosity to mass ratio which characterizes the star formation process. The histograms of the statistical distributions for these parameters are plotted in Fig. 3.

  

Figure 3: Histograms of the peak CO main beam brightness temperature a), size b), mean density c), mass d), IR luminosity to mass ratio e) and mean CS line width f) distributions for the CS cores observed at SEST and in Onsala located in the range 1 - 4 kpc from the sun (filled) and within 5 kpc from the sun (thick lines)

An inspection of these histograms leads to the following conclusions:

The CO brightness temperature distribution peaks at $\sim$20-30 K; for most cores ($\sim$90%) these temperatures lie in the range 15-50 K. Since the CO transitions are easily thermalized this temperature should be close to the kinetic temperature somewhere in the source (minus the background temperature). However, due to a very high optical depth in CO lines, the innermost regions can be shielded (if there is no significant velocity gradient or significant clumpiness). Therefore, the kinetic temperatures determined from CO might refer to the outer regions of the cores. It is worth noting, however, that they are rather close to the temperatures found from ammonia observations of HMSF cores in Effelsberg with a similar beam size (Zinchenko et al. 1997) which gave $T_{\rm kin}\approx 20-30$ K near the peaks of ammonia emission. These temperatures reflect the conditions in the dense gas where ammonia is excited (though averaged over the beam). The CO temperatures are also close to the colour temperatures of the embedded IRAS sources determined from the ratio of the 60 and 100 $\mu$m fluxes (Tables 4-6), i.e. the gas kinetic temperature is close to the temperature of cold dust component which emits at these wavelengths.

We present the size, mass and density distributions in the way which is typical for mass distribution, i.e. by the number density per unit (linear) interval of the parameter. This function for mass is called the mass spectrum and we can talk analogously about size and density spectra. Most cores have sizes of 1.0- 1.5 pc. There is no cores with  pc in the considered subsamples. It means in particular that the angular size of a typical core equals our beam size at the distance of 3-5 kpc which supports our selection of the distance limits since many of more distant cores would be unresolved.

The mean density of the cores is 10³-10⁵ cm^-3. We emphasize that this is an average density defined as $\bar{n}=N_{\rm L}(\mbox{H}_2)/L$.This density is, at least at the lower edge of the distribution, too low for effective CS excitation. The densities in the regions of line formation derived from multitransitional data comprise usually $\sim 10^6$ cm^-3 (e.g. Bergin et al. 1996; Plume et al. 1997). It is worth noting that the latter estimates are obtained assuming collisional excitation of CS molecules. One might think that in the vicinity of powerful IR sources radiative excitation via the lowest vibrational states can be important. However, as shown by Carroll & Goldsmith (1981), such IR pumping can affect the CS excitation only in regions of  pc around an IR source. This is much less than the typical size of the CS cores. Then, one can see in Fig. 2 that in many cases the CS emission peaks do not coincide with the IRAS sources; the displacements exceed the uncertainties in the IRAS positions which are typically $\sim 10\hbox{$^{\prime\prime}$}-20\hbox{$^{\prime\prime}$}$.Thus, the IR pumping is probably not important for most of our cores. Apparently, the significant difference between the mean densities and densities in regions of line formation implies strong density inhomogeneities in the cores. The fact that the mean densities are frequently lower than densities needed for noticeable CS excitation indicates that there must be practically empty voids in the cores and it is easy to see that 1-2 orders of magnitude difference between the mean density and the density in the emitting regions implies a correspondingly low volume filling factor for the CS emitting clumps.

The mass spectrum ${\rm d}N/{\rm d}M$ for  $M_\odot$ can be approximated by a power law ${\rm d}N/{\rm d}M\propto M^{-\alpha}$ with $\alpha = 1.6\ \pm\ 0.3$. This is very close to the slopes of clump mass spectra of individual molecular clouds which have been subject of several investigations (see, e.g., Blitz 1991 and references therein). They gave $\alpha$ from 1.4 to 1.7 for several giant molecular clouds. Most recently Kramer et al. (1998) found for 7 clouds that the $\alpha$ values lie between 1.6 and 1.8. However, our result does not refer to clumps in an individual cloud but to a sample of objects spread throughout the Galaxy. Moreover, the ranges of masses investigated in these studies are very different, $\sim$$10^{-4}-10^0~M_\odot$ in L 1457 (Kramer et al. 1998) as compared to $\sim$$10^3-3\ 10^{4}~M_\odot$ in the present work. The similarity in the slopes of the mass spectra in all these cases shows that it is really a universal law (unfortunately, unexplained yet).

The IR luminosity to mass ratio peaks at $\sim$10 $L_\odot/M_\odot$(we use here only the IRAS data of sufficiently high quality; the data with upper limits at 60 or 100 $\mu$m were omitted). Recently Plume et al. (1997) found an average value of 190 $L_\odot/M_\odot$ for objects of the same class which is an order of magnitude higher. The difference can probably be explained by the following factors:

(1) Plume et al. derive sizes and masses from the CS J=5-4 data. They are usually lower than the corresponding parameters derived from the J=2-1 line (e.g. Lapinov et al. 1998) since in higher transitions they see a smaller portion of the cloud. Most probably this is explained by density gradients in the cores (higher transitions require higher densities for excitation).

(2) Plume's et al. sources for which they derive the $L_{\rm IR}/M$ ratio are located mainly in the inner Galaxy while our distribution refers both to the inner and outer parts of the Galaxy. We show below that there is a significant gradient in this ratio along the galactocentric radius.

(3) Most of the sources selected by Plume et al. for this analysis belong to the very luminous objects with high star formation activity.

The distribution of the CS line widths which reflects the velocity dispersion in the cores shows at first that the internal movements are highly supersonic. If we recall the conclusion of a very low volume filling factor for the emitting clumps it would mean most probably that the line widths correspond to relative motions of these clumps. There are many arguments in favour of this model. Their discussion is beyond the scope of the present paper. Some of them concern the line broadening which is considered below.

4.4 Galactic gradients of the core parameters

In Paper II we found a trend for decreasing mean density of the cores with increasing galactocentric distance R. The data were limited to a rather narrow interval, $R\approx 7-11$ kpc. The present Onsala results extend this interval significantly. In addition, Juvela (1996) performed similar observations in the inner Galaxy ($R\approx 4-8$ kpc). However, he used additional selection criteria for the IR flux so that we cannot directly incorporate his data. Some of the Onsala sources lie as far as at $R\sim$20 kpc. However, we exclude these very distant objects and limit ourselves to  kpc.

The distribution of the investigated objects in the galactic plane is shown in Fig. 4 where we include also Juvela's sources.

  

Figure 4: Distribution of the detected sources in the galactic plane. The lightly shaded area corresponds to the range of galactic longitudes investigated by Juvela (1996). The heavily shaded part has not been included in our study. The size of the markers is proportional to $\log{\bar{n}}$ for the cases where the density has been derived. In other cases the objects are shown by dots. The solid line shows the solar circle. The dashed circle corresponds to the distance 5 kpc from the sun

  

Figure 5: Dependences of the peak CO main beam brightness temperature a), size b), mean density c), mass d), IR luminosity to mass ratio e) and mean CS line width f) on the galactocentric distances for the CS cores observed at SEST (filled squares), Onsala (triangles and dots; dots mark the category II data for mass and density, the other data are indicated by triangles) and Metsähovi radio telescope (open squares). The broken lines in panels b), c), e) show the average values in 1 kpc bins. The error bars correspond to standard deviations of the data in the bins

In Fig. 5 we plot the core parameters (peak CO main beam temperature, size, density, mass and mean CS line width) in dependence on the galactocentric radius using the SEST, Onsala and Metsähovi data. We use here the category II data for mass and density (i.e. assuming LTE mass equal to virial mass) since as shown above the assumption of $M=M_{\rm vir}$ is in general correct. An inspection of Fig. 5 shows that these data (marked by dots) are well aligned with the other results and do not influence significantly the dependences. The Metsähovi estimates of the mass and density have been slightly corrected using the same procedure as for the other data. Then, for NGC 281 we use our new C³⁴S results (Table 3).

The most noticeable feature in the plots is the apparent decrease of the mean density with R. It seems to be linear in the $\log(\bar{n})-R$coordinates so we approximated the dependence by the function  

$$\bar{n}=n_0\ {\rm e}^{-(R/R_{\rm n})}.$$ (1)

The best least squares estimates for the parameters are $n_0=(3.7\pm 0.5)\, 10^5$ cm^-3, $R_{n}=2.7\pm 0.6$ kpc. If we consider only the sources within 5 kpc from the sun we obtain $n_0=(2.2\pm 0.3)\, 10^5$ cm^-3, $R_{n}=3.4\pm 0.8$ kpc. The Pearson's correlation coefficient in both cases is $r\approx -0.5$.Using the standard statistical methods (e.g., Bendat & Piersol 1986) we obtain that the hypothesis of zero correlation is rejected at $\sim$0.002% level of significance for the whole sample, i.e. the correlation is very significant.

However, strictly speaking this conclusion is valid assuming binormal distribution of the variables. In our case the distributions differ seemingly from that. Bearing this in mind we consider also nonparametric or rank correlation which is more robust than linear correlation (Numerical Recipes 1992). For the $R-\log{\bar{n}}$ relationship the result is practically the same: the Spearman rank-order correlation coefficient is $r_{\rm s}\approx -0.50$ and the hypothesis of zero correlation is rejected at $\sim$0.01% level of significance.

As discussed in Paper II this trend should not be due to the beam dilution or selection effects because their influence should be more or less symmetric relative to the Sun position. In principle, such a trend could arise from a possible galactic gradient of CS abundance since the LTE masses are calculated assuming a constant value of $\chi {\rm (CS)}=4\ 10^{-9}$ (Irvine et al. 1987). However, in this case we would see a similar trend in the $M/M_{\rm vir}$ ratio because M depends on $\chi {\rm (CS)}$ while $M_{\rm vir}$ does not. We found no dependence of this ratio on R as can be seen in Fig. 6, which excludes a significant gradient in the CS abundance.

  

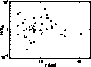Figure 6: The ratio of LTE mass to virial mass versus the galactocentric distance. The marks are the same as in Fig. 5

There is no dependence of the core mass on R. At the same time there is a noticeable increase of the core size with R which is consistent with the density decrease and constant mass. The Spearman correlation coefficient is $r_{\rm s}\approx 0.37$ and the hypothesis of zero correlation is rejected at $\sim$0.5% level of significance. Another parameter which changes noticeably is the $L_{\rm IR}/M$ ratio. In this case $r_{\rm s}\approx -0.35$ but the number of the data points is lower than in the previous cases. The hypothesis of zero correlation is rejected at $\sim$3% level of significance. This ratio varies in about the same proportion as the mean density. The least-squares fit gives the scale length $R_{\rm L/M}= 3.6\pm 1.2$ kpc. It is worth noting the the robust linear fit to the data minimizing absolute deviations (Numerical Recipes 1992) gives the scale length of about 2.9 kpc for both $R-\bar{n}$ and $R-L_{\rm IR}/M$ dependences.

The CO brightness temperature and CS line width do not change significantly in the considered range of galactocentric distances (7 kpc  kpc). As mentioned above, Juvela (1996) performed similar observations in the inner Galaxy. Since he selected the most IR luminous objects we cannot incorporate his data directly. Anyway, the comparison of his results with our data is rather informative and we present this in Fig. 7. Here we limit ourselves to the sources located within 5 kpc from the sun. Then, we do not use the original Juvela's density estimates but the densities derived from virial masses as for our category II sources. The masses are also represented by virial masses. We prefer to do it in this way since Juvela estimated masses and densities from C³⁴S maps, not from CS maps as in our case. For the same reason we increased Juvela's estimates of sizes by a factor of 1.3 which is a mean ratio of the CS sizes to C³⁴S ones.

  

Figure 7: The same as in Fig. 5 with inclusion of Juvela's (1996) data (diamonds) and with a distance limit of d<5 kpc

One can see that Juvela's points are consistent with the trends mentioned above, i.e. the gradients in the mean density and $L_{\rm IR}/M$ ratio. In addition, in Juvela's sample the line widths are noticeably larger on the average. There are practically no sources with such broad lines among those studied in Paper I and here. However, due the additional selection by IR flux we cannot exclude the possibility that Juvela's points represent only the upper parts of the distributions.

To summarize, the available data are consistent with an exponential decrease of the mean core density with the galactocentric radius for $R\approx 7-14$ kpc. The characteristic scale length is $\sim$3 kpc. It is accompanied by a corresponding increase of the core size. The IR luminosity to mass ratio changes probably in about the same proportion as the mean density. The velocity dispersion in the cores probably increases towards the inner Galaxy at least at  kpc.

How does this relate to other studies? Several years ago we found a strong gradient in the HCN detection rate versus the galactocentric radius for a sample of molecular clouds associated with Sharpless H II regions (Zinchenko et al. 1989). It is probably consistent with the density gradient found here (a more definite conclusion should rely on HCN excitation analysis).

Galactic gradients of molecular cloud properties have been a subject of several other studies in recent years (see, e.g., discussions in Helfer & Blitz 1997 and Sakamoto et al. 1997). Briefly, the results are somewhat contradictory but there are unambiguous gradients in the HCN/CO, CS/CO (Helfer & Blitz 1997) and HCO⁺/¹³CO (Liszt 1995) emission line ratios which resemble our HCN result mentioned above. While Liszt interprets his result as an abundance effect, Helfer & Blitz conclude that the contrast between the bulge and the disk is most likely caused by a combination of higher gas densities as well as higher kinetic temperatures in the bulge.

The most recent extensive CO J=2-1 survey by Sakamoto et al. (1997), when combined with the Columbia CO J=1-0 survey performed with the same angular resolution, shows a gradient in the CO(J=2-1)/CO(J=1-0) line ratio which is interpreted by the authors as an evidence of gradient in the high-density to low-density gas ratio.

Kislyakov & Turner (1995) found no gradient in the ratio of the C¹⁸O(J=2-1) and C¹⁸O(J=1-0) line intensities for a sample of 11 clouds associated with Sharpless H II regions. Even if correct despite the low volume of the sample, this result does not contradict our findings since this ratio is governed by the gas density in regions of line formation while our result refers to the mean gas density in the source. If the objects are clumpy the mean density can change while the C¹⁸O(J=2-1)/C¹⁸O(J=1-0) line ratio remains constant.

There are other indications for a galactic gradient in the cloud properties. E.g. a recent survey of thermal SiO emission (indicative of shocks) by Harju et al. (1998) shows much higher SiO line intensities in the inner Galaxy.

It is also worth noting that the exponential component of the stellar galactic disk has a scale length of $\sim$2.6 kpc (Freudenreich 1998) which is very close to our value for the mean density distribution. At last, we note that the overall distribution of molecular gas traced by CO can be more appropriately described as a truncated exponential with a scale length of 2.8 kpc than a "molecular ring'' (Blitz 1997). Thus, we obtain a picture where both the total surface density of molecular gas as well as the mean density of the cores drop with increasing galactocentric radius according to an exponential law with a scale length of $\sim$3 kpc. The star formation efficiency, as described by the IR luminosity to mass ratio, behaves seemingly in a similar way. Most probably these coincidences are not accidental.

What can be the physical reason for this behaviour? We suppose that the most probable explanation involves an influence of galactic density waves responsible for the formation of the spiral structure as suggested already by Sakamoto et al. (1997). The normal velocity at which gas enters the shock front associated with the density wave is higher in the inner Galaxy and also the frequency at which the shock waves of an m-armed spiral encounter the gas increases inwards leading to higher degree of gas compression.

4.5 Comparison of the CS and C³⁴S data

We can obtain important implicit information about the internal core structure by comparing intensities and line widths of different isotopomers (e.g. Zinchenko et al. 1994). In general the line widths are closer to each other in clumpy clouds. In Fig. 8 the ratio $\Delta V$(CS)/$\Delta V$(C³⁴S) is plotted versus the $T_{\rm mb}{\rm (C^{34}S)}/T_{\rm mb}{\rm (CS)}$ ratio. We use here only the SEST and Onsala data with the highest signal to noise ratios and apparently simple line profiles. The solid line corresponds to an uniform LTE model with the terrestrial abundance ratio (22.5). The line broadening was calculated as in Zinchenko et al. (1994). The dashed line corresponds to the ratio of the effective optical depths in CS and C³⁴S lines equal to 10. The reduction of this ratio in respect to the terrestrial value can be caused either by the abundance effects or by clumpiness (e.g. Martin et al. 1984).

  

Figure 8: The ratios of the CS and C34S line widths versus $T_{\rm mb}{\rm (C^{34}S)}/T_{\rm mb}{\rm (CS)}$ ratio for the SEST (filled squares) and Onsala (triangles) samples. The solid line corresponds to an uniform LTE model with the terrestrial abundance ratio. The dashed line corresponds to a model with the ratio of the effective optical depths in the two lines equal to 10

Though a few points lie close to the predictions of the first model and even more are closer to the second one, in general there is no systematic trend for increasing the line width ratio with increasing $T_{\rm mb}{\rm (C^{34}S)}/T_{\rm mb}{\rm (CS)}$ ratio. So we can apparently reject an uniform model with any ratio of the optical depths and concentrate on other alternatives. In the framework of clumpy models we need apparently a set of clumps with different ratios of the optical depths. It seems to be possible to reproduce the presented results by varying the clump properties and the number of clumps on the line of sight. However, the discussion of clumpy models is beyond the scope of this paper. One of the main caveats on this way is the apparent smoothness of the line profiles as discussed e.g. recently by Tauber (1996). We leave a quantitative analysis until further publications.

Attempts for alternative explanations can be based on the assumption of line broadening by systematic motions or on non-uniform models with a smooth density distribution. The main kinds of systematic motions include collapse, expansion, rotation and outflows. The line widths of different isotopomers will be naturally close to each other in this case. The usual statistical arguments against the collapse as a main line broadening factor can be overwhelmed perhaps if we take into account that most of the contracting mass is ejected again via high-velocity outflows which are common in these regions (as suggested by A.V. Lapinov in a private communication). However, collapse should produce "kinematic signs'' on the line profiles, e.g. red-shifted (or in some cases blue-shifted as shown by Zinchenko & Lapinov 1985) self-absorption dips which are not evident in our sample.

In microturbulent non-uniform models one can assume that the core itself is optically thin in both lines but the CS line is weakened in a diffuse envelope leading to an increase of the $T_{\rm mb}{\rm (C^{34}S)}/T_{\rm mb}{\rm (CS)}$ ratio. It seems to be necessary to assume that the velocity dispersion in the envelope is much higher than in the core which is unrealistic. Furthermore, the measured C³⁴S column densities imply high optical depths in the CS lines.

We conclude that small scale clumpiness seems to be the most plausible explanation for the presented results with systematic motions being the best possible alternative.

4.6 CS cores and H₂O masers

Our SEST data as well as Juvela's data have shown a slight asymmetry in the distribution of the velocity difference of the masers and CS cores with the maser velocities being more negative on the average. In the present Onsala sample we do not see such asymmetry. In Fig. 9 we plot the histogram of $V(\mbox{H$_2$O})-V(\mbox{CS})$ values for the combined SEST+Onsala data set. The distribution is practically symmetric. However, this plot shows that the difference in the velocities can be quite large (the standard deviation is $\sim$7 kms^-1 if we neglect 2 masers with the highest velocity differences). Thus, H₂O masers are moving with high velocities relative the CS cores.

  

Figure 9: Histogram of the differences between the H2O and CS velocities for the combination of the SEST and Onsala samples