2 Infrared variability

2.1 Data

BL Lacertae has been observed in the near-infrared bands (J, H, and K) for about 20 years. The data from the literature listed in Table 1 and the 38 K band data derived from the paper of Soifer & Neugebauer (1980) are discussed in this paper. Table 1 gives the observer(s) in Col. 1; the number of data points in Col. 2, and the telescope(s) used in Col. 3.

  

Table 1: Literature of the near-infrared data for BL Lacertae

2.2 Variations

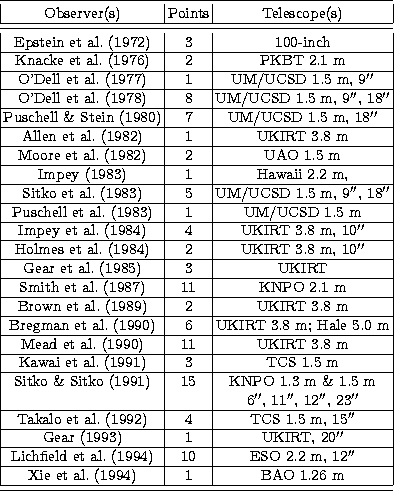
BL Lacertae is located at $b=-10^{\circ}$ and thus has a reddening due to our own galaxy. According to the model of Sandage (1972), $A_V = 0.165(1.192- \tan{b})\csc{b}$, for $\vert b\vert \leq 50^{\circ}$, we have A_V=0.97. Following the reddening curve (Cruz-Gonzalez & Huchra 1984, see also Whitford 1958): $A(\lambda)=A_{V}(0.11\lambda^{-1}+0.65\lambda^{-3}-0.35\lambda^{-4}$, we can get A_J=0.267 mag, A_H=0.158 mag, and A_K=0.092 mag. After the correction, we got the infrared (J, H, and K bands) light curves and show them in Fig. 1. The largest infrared amplitude of variability in the J, H, and K bands: $\Delta J = 2\hbox{$.\!\!^{\rm m}$}29(10.47-12.76)$, $\Delta H = 2\hbox{$.\!\!^{\rm m}$}42 (9.60-12.02)$, $\Delta K = 2\hbox{$.\!\!^{\rm m}$}93 (8.47-11.30)$ have been obtained from the available data. There is no correlation between color index and brightness; although there is some tendency of J-H increasing with J, it is far from being conclusive (see Figs. 2a-c).

  

Figure 1: a) The long-term J light curve of BL Lacertae, b) The long-term H light curve, c) The long-term K light curve, some early data are derived from the paper of Soifer & Neugebauer (1980)

  

Figure 2: a) Plot of J against J-H; b) Plot of J against H-K; c) Plot of J against J-K; d) Color-Color Plot of J-H vs. H-K; e) Color-Color Plot of J-H vs. J-K. The straight line is for the best fit line; f) Color-Color Plot of J-K vs. H-K. The straight line is for the best fit line

For color indices, we have got strong correlations of J-H vs. J-K and J-K vs. H-K: $J-K = (1.15\ \pm\ 0.02) (J-H) + 0.68\ \pm\ 0.01$ with a Spearman Rank Correlation coefficient of r=0.702 and a probability of the correlation having occurred by chance $p= 1.3 \ 10^{-8}$; $H-K = (0.57 ~\pm ~ 0.003) (J-K) -0.12 ~ \pm ~0.01$ with r=0.796 and $p= 1.4 \ 10^{-12}$, but no correlation was found for J-H vs. H-K (see Figs. 2d-f). We also found that the average values of color indices are $J-H = 0.78 \pm 0.11$ (65 data), $H-K = 0.78 \pm 0.12$ (71 data), and $J-K = 1.55 \pm 0.13$ (63 data). One set of data J= 11.56, H = 11.72, and K =10.26 (Sitko et al. 1983) are not included in Fig. 2 because the color index of J-H = 0.23 is much lower than the average value. If we only consider the data with known apertures and make the aperture correction according to the method of Sandage (1972), there is no correlation between color index and magnitude or between J-H and H-K either.