

Up: Atomic data from the
In order to analyse collisional data and to present them in compact form,
BT introduce a scaling procedure where the collision strength 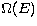 is
mapped onto the reduced form
is
mapped onto the reduced form 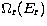 , where the infinite
energy E
range is scaled to
the finite
, where the infinite
energy E
range is scaled to
the finite  interval (0,1). For a quadrupole transition,
such as
interval (0,1). For a quadrupole transition,
such as  D
D 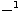 S in Ar III, the BT scaling prescription
is
given by
S in Ar III, the BT scaling prescription
is
given by
|  |
(1) |
| (2) |
with  being the transition energy, E the electron energy
with respect to the reaction threshold and C an adjustable scaling parameter.
A key aspect of the BT approach lies in the fact that the limiting points
being the transition energy, E the electron energy
with respect to the reaction threshold and C an adjustable scaling parameter.
A key aspect of the BT approach lies in the fact that the limiting points
 and
and 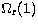 are both finite and can be
computed. BT have
discussed that for a quadrupole transition these points are
are both finite and can be
computed. BT have
discussed that for a quadrupole transition these points are
|  |
(3) |
| (4) |
where 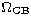 is the Coulomb-Born high-energy limit. This formalism
can also be extended to treat the effective collision strength
is the Coulomb-Born high-energy limit. This formalism
can also be extended to treat the effective collision strength
|  |
(5) |
through the analogous relations
| 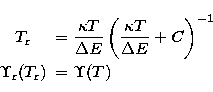 |
(6) |
| (7) |
where T is the electron temperature and  the Boltzmann constant;
the limiting points now become
the Boltzmann constant;
the limiting points now become
|  |
(8) |
| (9) |
A second important point in the BT approach is that the reduced effective
collision strength can be neatly fitted in its entire range. A 5-point
spline is usually sufficient, and thus leads to a notably compact way
of presenting collisional data.
With specific reference to the questioned transition in Ar III, BCT
have computed a Coulomb-Born high-energy limit of
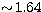 . This computation includes configuration interaction effects
that are found only to cause changes of a few per cent. Then, in a plot of
the IP-X effective collision strengths, they
scale the fairly low temperature range of 0 - 105 K to occupy 90%
of the reduced temperature interval and they find an extrapolated high-energy
limit of
. This computation includes configuration interaction effects
that are found only to cause changes of a few per cent. Then, in a plot of
the IP-X effective collision strengths, they
scale the fairly low temperature range of 0 - 105 K to occupy 90%
of the reduced temperature interval and they find an extrapolated high-energy
limit of 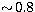 , a factor of 2 lower than the Coulomb-Born limit,
which led them to question the accuracy of the calculation.
, a factor of 2 lower than the Coulomb-Born limit,
which led them to question the accuracy of the calculation.


Up: Atomic data from the
Copyright The European Southern Observatory (ESO)




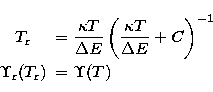

![]() . This computation includes configuration interaction effects
that are found only to cause changes of a few per cent. Then, in a plot of
the IP-X effective collision strengths, they
scale the fairly low temperature range of 0 - 105 K to occupy 90%
of the reduced temperature interval and they find an extrapolated high-energy
limit of
. This computation includes configuration interaction effects
that are found only to cause changes of a few per cent. Then, in a plot of
the IP-X effective collision strengths, they
scale the fairly low temperature range of 0 - 105 K to occupy 90%
of the reduced temperature interval and they find an extrapolated high-energy
limit of ![]() , a factor of 2 lower than the Coulomb-Born limit,
which led them to question the accuracy of the calculation.
, a factor of 2 lower than the Coulomb-Born limit,
which led them to question the accuracy of the calculation.