Various automatic detection methods such as binarization and thinning, Sobel filters and logical feature filters give incomplete results so far (Smareglia et al. 1994). Our approach is based on signal processing methods (Bratsolis 1997).
In the case of images obtained from objective prism plates, the objects to analyze (the stellar spectra), although possessing a great variety of internal structural characteristics, show some evident common features. For the detection of a spectrum, the most important feature is its beginning that is characterized by the presence of intense gradients. So, the main problem of the detection is reduced to the determination of the beginning of the spectrum.
Let us consider an objective prism image (Fig. 1a).
It contains spectra of bright and faint stars, single or overlapped,
and a random noise.
This is a part of the digitized spectral plate, a subimage of ![]() pixels.
Let I(x,y) denote the value of the pixel (x,y) where the x-axis is down the dispersion.
The subimage itself can be considered as a
set of M discrete one-dimensional signals Iy(x)=I(x,y), where M is the number of rows and
every signal is an independent row y.
The energy Ey of a particular one-dimensional signal is defined by Eq. (1).
pixels.
Let I(x,y) denote the value of the pixel (x,y) where the x-axis is down the dispersion.
The subimage itself can be considered as a
set of M discrete one-dimensional signals Iy(x)=I(x,y), where M is the number of rows and
every signal is an independent row y.
The energy Ey of a particular one-dimensional signal is defined by Eq. (1).
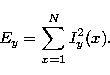 |
(1) |
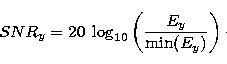 |
(2) |
We find it by taking the derivatives and choosing the maximal. In advance, we apply to the signal an appropriate composition of median and average filters resulting in an optimally-smoothed spectrum scan (Fig. 1e) with its derivative shown in Fig. 1f. The latter is used to determine the very beginning of the spectrum. We overcome the problem of absorption lines by considering the maximal derivative in every case at a point which is leftward from the maximum value of the row. The final results of spectra detection on this subimage are illustrated in Fig. 1c.
It can easily be seen that the sizes of the subimage, especially down the wavelength direction, is of crucial importance for the algorithm just described. To avoid missing two spectra on the same row, the subimage should be shorter than the spectrum length. Fixing the subimage length, we have to put some restriction on its width, to take into account the local signal-to-noise ratio that gives the best detection limits for the peak-picking process. Both these imply that an image frame should be handled in pieces, subframes.
Taking a subframe from an image, there are often spectra that begin near the subframe's left or right end or are crossed by the bottom or top side. Such spectra probably could not be detected. To avoid this, a partial overlapping of the subframes should be applied in both axes. Having in mind the spectral image parameters, it is optimal to set the subframe sizes to a value about the half of the spectral length, whereas the overlapping size to about twice of the spectral width.
Copyright The European Southern Observatory (ESO)