3 Remarks on the individual Cepheids

YZ Aurigae
The presence of a photometric companion has already been suspected by Madore (1977) and Madore & Fernie (1980). The additional light from a blue companion star has been confirmed by Szabados (1998) based on the wavelength dependence of the photometric amplitudes in U, B, V and R bands.

  

Table 2: O-C residuals for YZ Aur

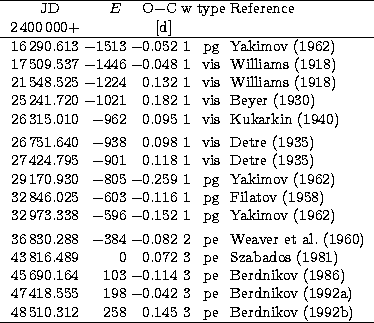
The radial velocity of YZ Aur was measured at two epochs (Joy 1937, and present paper) separated by an interval longer than 20000 days. (In addition, there are two recent data published by Gorynya et al. 1992a). Although the descending branch of the radial velocity phase curve is not covered by recent data (see Fig. 1), the systematic shift in the $\gamma$-velocity is obvious between the two data series.

The new value of the pulsation period has been determined from the data collected in Table 2. The revised elements for the normal maxima are as follows: The radial velocity phase curve is shown plotted in Fig. 1 using this revised value of the pulsation period.

  

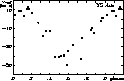Figure 1: Radial velocity curve of YZ Aur using the revised pulsation period of 18.192830 days. Zero phase was arbitrarily chosen at JD2400000 for each radial velocity phase curve presented in this paper. Open circles denote Joy's (1937) data, asterisks mean Gorynya et al.'s (1992a) observations, while filled circles are used for showing data listed in the present paper

  

Table 3: O-C residuals for AS Aur

AS Aurigae
As to the photometric data, this Cepheid has been very much neglected (see Table 3) but fortunately there are two radial velocity measurement series widely separated in time (Joy 1937, and present paper) showing discordant $\gamma$-velocity values (see Fig. 2). Because the photometric observational material also spans a time interval longer than half a century, the phase matching can be considered as reliable when using the revised pulsation period. The scanty photometric data led to the following elements for the moments of brightness maxima:

  

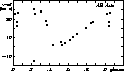Figure 2: Radial velocity curve of AS Aur folded on the revised pulsation period of 3.175001 days. Open circles: Joy's (1937) data, filled circles: present paper

AA Geminorum
Being the brightest Cepheid in this sample, AA Gem has a long record of photometric observations (see Table 4), therefore the new ephemeris is very reliable: The photometric duplicity indicators led to controversial results: Madore's (1977) loop-method does not indicate a (blue) companion while the phase-method (Madore & Fernie 1980) refers to a photometric companion. In their recent study, Evans & Udalski (1994) conclude that the two faint companions are only optical, i.e. physically unrelated to AA Gem. The available two radial velocity datasets, however, result in significantly discordant $\gamma$-velocities (see Fig. 3): Joy's (1937) velocity data fall below the recent data by more than 10 km s^-1 on the average.

  

Table 4: O-C residuals for AA Gem

  

Figure 3: Radial velocity curve of AA Gem using the revised pulsation period of 11.302450 days. Symbols are the same as in Fig. 2

TX Monocerotis
Pel's (1978) multicolour photometry indicated the presence of a companion but no detailed spectroscopic study of this Cepheid has been performed yet. Vinkó (1991) searched for evidence of a companion in the O-C diagram of TX Mon but the scatter due to inaccuracy of the early photometric data do not allow to reveal the light-time effect, if any. He approximated the O-C graph by a parabola assuming a continuous minor increase in the pulsation period. Here the pulsation period is assumed to be constant and the resulting linear ephemeris (determined from the data in Table 5) is as acceptable as Vinkó's parabolic one.

The available radial velocity data, however, clearly show the effect of a physical companion (see Fig. 4). Not only are Joy's (1937) velocity values systematically smaller than the "normal'' value of the corresponding phase of the second-epoch radial velocity curve but the recent high-precision data collected during a time interval as short as four years show a wide scatter, indicating variations in the $\gamma$-velocity due to orbital motion. The number of the available data points justified that a search for periodicity be performed, in order to obtain a preliminary value of the orbital period. A Lafler-Kinman-type algorithm (Lafler & Kinman 1965) indicates that the orbital period is near 470 days (the uncertainty being as large as $\pm$30 days), and longer periods can be excluded. This means that TX Mon is a classical Cepheid with one of the shortest known orbital period. A Fourier-type algorithm (Deeming 1975), however, could not confirm this preliminary value but no other value for the orbital periodicity could be guessed.

  

Table 5: O-C residuals for TX Mon

  

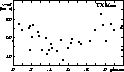Figure 4: Radial velocity curve of TX Mon folded on the revised pulsation period of 8.701903 days. Symbols are the same as in Fig. 2

V495 Monocerotis
The faintest Cepheid in this sample has only a brief history of observations. Even the pulsation period could not be improved based on the available photometric data covering only a decade, so the value of 4.096583 days, published in the GCVS, has been used.

The radial velocity data obtained by the ELODIE-spectrograph (Pont et al. 1997) are plotted in Fig. 5. It is clearly seen that the data show an annual shift, indicative of the orbital motion of the Cepheid around the mass centre of a binary system. Since these data were acquired within two consecutive observational seasons, any subtle error in the pulsation period cannot modify this conclusion. Duplicity of V495 Mon, however, has to be confirmed by further radial velocity data because the present data have been obtained at the brightness limit for the ELODIE, and the correlation functions sometimes were not very clean.

  

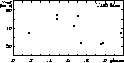Figure 5: Radial velocity curve of V495 Mon folded on the pulsation period of 4.096583 days. All observations were obtained by Pont et al. (1997). Filled circles denote radial velocity data taken in Nov. 1993/Mar. 1994, open circles are the data from Dec. 1994-Jan. 1995

CS Orionis
The updated ephemeris determined from the data listed in Table 6 is as follows: The photometric amplitudes in U, B, V, and R bands indicate the presence of a blue companion (Szabados 1998).

This companion may be responsible for the orbital effect detectable in the radial velocity data (see Fig. 6). The difference between the mean velocity averaged over one pulsational cycle exceeds 20 km s^-1, if Joy's (1937) and the recent data are compared.

  

Table 6: O-C residuals for CS Ori

  

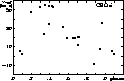Figure 6: Radial velocity curve of CS Ori folded on the revised pulsation period of 3.889281 days. Symbols are the same as in Fig. 2

UX Persei
The revised ephemeris determined from the data appearing in Table 7 is as follows: Although Madore's (1977) loop-method, based on the U-B and B-V colour indices, does not indicate the presence of a secondary star, UX Per seems to have a photometric companion based on the phase-method (Madore & Fernie 1980).

The radial velocity data clearly indicate a spectroscopic companion (see Fig. 7): Joy's (1937) data are systematically less negative (but a single point) than the CORAVEL-measurements, the difference being significant, about 15 km s^-1.

  

Table 7: O-C residuals for UX Per

  

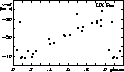Figure 7: Radial velocity curve of UX Per folded on the revised pulsation period of 4.565733 days. Symbols are the same as in Fig. 2

VW Puppis
The revised ephemeris based on the photometric data (see Table 8) is quite precise: The variation in the $\gamma$-velocity caused by the orbital motion is the largest in this sample (see Fig. 8): the difference between Joy's (1937) and the CORAVEL-data of the corresponding phase is about 25 km s^-1. A closer inspection of the CORAVEL-data reveals that even an annual shift is noticeable: an increase of about 1 km s^-1 in the $\gamma$-velocity is observed in this homogeneous dataset.

  

Table 8: O-C residuals for VW Pup

  

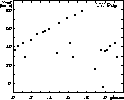Figure 8: Radial velocity curve of VW Pup folded on the revised pulsation period of 4.285298 days. Symbols are the same as in Fig. 2