The basic information on the input physics of the models can be found in
Claret 1995 (Paper I). The masses of the models shown
here range from 1 to 40 ![]() . Convective core overshooting was
taken into account for models with
. Convective core overshooting was
taken into account for models with ![]() . For the
adopted initial metal content of Z = 0.004, we have computed models with
an initial content of hydrogen of 0.65, 0.744 and 0.80. The middle value
of 0.744 was selected on the basis of the enrichment law
. For the
adopted initial metal content of Z = 0.004, we have computed models with
an initial content of hydrogen of 0.65, 0.744 and 0.80. The middle value
of 0.744 was selected on the basis of the enrichment law ![]() Z for a primordial helium abundance of 0.24 and an
enrichment ratio of 3. The grids with X=0.65 and 0.80 provide the
necessary range for parametric studies and interpolation of different
chemical composition the latter being obviously artificial from the
astrophysical point of view since the corresponding helium content is not
compatible with the generally accepted values of the primordial helium
abundance. However, it is useful to interpolate the properties of models
with intermediary chemical composition.
Z for a primordial helium abundance of 0.24 and an
enrichment ratio of 3. The grids with X=0.65 and 0.80 provide the
necessary range for parametric studies and interpolation of different
chemical composition the latter being obviously artificial from the
astrophysical point of view since the corresponding helium content is not
compatible with the generally accepted values of the primordial helium
abundance. However, it is useful to interpolate the properties of models
with intermediary chemical composition.
Figures 1-3 show our usual HR diagrams for the three grids (X65, X744, X80) where the influence of the mean molecular weight on the morphology of the tracks is clear. In fact, by using simple homology relationships it is possible to understand qualitatively the behaviour of radius, effective temperature and luminosity of the models (see previous papers of this series).
The less massive models were computed until just before the helium flash, while the more massive ones were followed up to the core helium burning (in some cases, even until the first stages of carbon burning). However, for the sake of clarity, the blue loops for the more massive models were not plotted in Figs. 1-3. As it is well known, lower metallicity models present more extended blue loops, and we wanted to check their behaviour for fixed values of the mass and the metal content. Figure 4 shows the effect of changing the initial abundance of helium. The extension of the blue loops is presented for different values of initial helium for models of a 6 solar masses star. The blue loops are more extended as the value of Y increases. The existence and extension of blue loops depend on factors such as the central helium burning time scale, the corresponding one for shell burning and, of course, on the available amount of helium. Results shown in Fig. 4 were obtained by integration of the stellar structure equations using a grid of almost 4000 points in order to avoid problems with the chemical composition profiles.
We can see in Fig. 5 the dependency of the main-sequence lifetime on the initial hydrogen content for the three grids presented here. As expected, for a fixed metallicity, the largest lifetime corresponds to the largest initial hydrogen content.
Concerning the structural stellar parameters, we have computed the apsidal
motion constants (integrating the Radau equation), the moment of inertia and
the potential energy. As commented in Paper II we have also introduced in
our stellar evolutionary code the corresponding equations to compute
internal parameters which are used to calculate the synchronization and
circularizations times in binary systems. These parameters are related with
the equilibrium and the dynamical tides. In the case of the equilibrium
tides the turbulent dissipation was identified as the agent of
synchronization and circularization of orbits in binaries presenting
convective envelopes. In order to compute the time scales for
synchronization and circularization, we have to calculate the constant
![]() which depends on the physical properties of the stellar
envelope. Indeed, following the mixing-length approximation, the constant
which depends on the physical properties of the stellar
envelope. Indeed, following the mixing-length approximation, the constant
![]() can be written as (Zahn 1989)
can be written as (Zahn 1989)
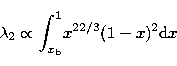 |
(1) |
The mechanism used to investigate the tidal evolution of stars with convective core and radiative envelopes is the radiative damping which is characterized by the tidal torque constant E2. The calculation of such a parameter is more problematic since it depends, among other intermediary calculations, on the derivative of the Brunt-Väisäla frequency just in the boundary of the convective core. For little evolved models, near the ZAMS, the computations are relatively simple. When a star in these conditions evolves, the convective core recedes and a large chemical composition gradient appears. Such gradients are responsible for the numerical difficulties to compute the tidal torque constant.
As E2 depends strongly on the physical conditions just at the boundary of the
convective core, one should expect differences between models with and
without core overshooting. Figure 7 illustrates the situation for
models with 10 ![]() . The model computed adopting core overshooting
present values of E2 slightly larger than the standard one (about 0.1 dex
as a average). This difference is not distinguishable at the present data
quality of synchronization and circularization levels.
. The model computed adopting core overshooting
present values of E2 slightly larger than the standard one (about 0.1 dex
as a average). This difference is not distinguishable at the present data
quality of synchronization and circularization levels.
In order to maintain a coherent format with respect to the previous models
of this series published in the WWW page of CDS at Strasbourg the values
of ![]() and E2 are not given. Interested readers can send their
request sending a message to claret@iaa.es.
and E2 are not given. Interested readers can send their
request sending a message to claret@iaa.es.
Acknowledgements
The Spanish DGYCIT (PB94-0007 and PB96-0840) is gratefully acknowledged for support during the development of this work.
Copyright The European Southern Observatory (ESO)